Flächeninhalt und Umfang/Flächeninhalt durch Auslegen mit Einheitsquadraten bestimmen: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 75: | Zeile 75: | ||
Ergänze bei deinem Eintrag die beiden Beispiele aus dem Video. Zeichne dazu die ursprünglichen Figuren ab und trage dort die Einheitsquadrate ein. Mache beim zweiten Beispiel farbig deutlich, welche beiden Flächen jeweils zusammen die Größe von einem Einheitsquadrat haben.|Üben}} | Ergänze bei deinem Eintrag die beiden Beispiele aus dem Video. Zeichne dazu die ursprünglichen Figuren ab und trage dort die Einheitsquadrate ein. Mache beim zweiten Beispiel farbig deutlich, welche beiden Flächen jeweils zusammen die Größe von einem Einheitsquadrat haben.|Üben}} | ||
| Zeile 110: | Zeile 88: | ||
# [[Flächeninhalt und Umfang/Flächeninhalte von zusammengesetzten Flächen bestimmen]]}} | # [[Flächeninhalt und Umfang/Flächeninhalte von zusammengesetzten Flächen bestimmen]]}} | ||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Flächeninhalt]] | |||
Version vom 20. April 2020, 11:56 Uhr
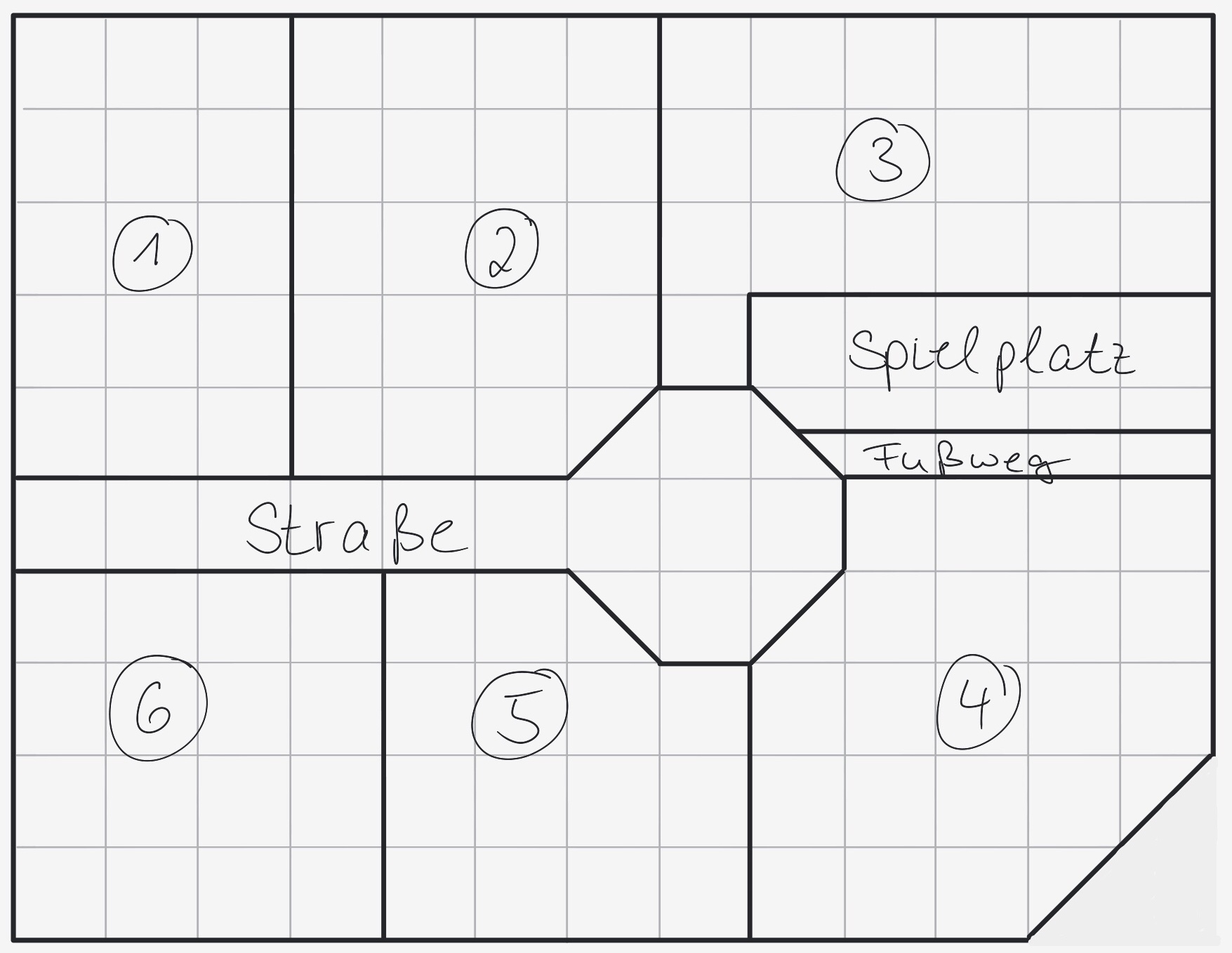
Ein Bauplatz für Familie Schulte
Herr und Frau Schulte möchten in einem Neubaugebiet ein Grundstück kaufen. Auf dem Bild siehst du eine Skizze des Baugebiets. Noch sind alle sechs Bauplätze frei. Je größer ein Grundstück ist, desto mehr muss man dafür bezahlen!
Die vier Familienmitglieder haben unterschiedliche Vorstellungen vom perfekten Grundstück:
Felix: "Rechtecke sind langweilig. Wir sollten das Grundstück kaufen, das die meisten Ecken hat!"
Ella: "Ich möchte direkt am Spielplatz wohnen!"
Frau Schulte: "Mir gefallen alle Grundstücke. Wir sollten das günstigste Grundstück kaufen."
Herr Schulte: "Ich möchte ein großes Gemüsebeet anlegen. Wir sollten das größte Grundstück kaufen."
Beantworte die Fragen und überprüfe!
Welche beiden Familienmitglieder entscheiden sich für das gleiche Grundstück? (!Felix und Ella) (!Felix und seine Mutter) (Felix und sein Vater) (!Ella und ihre Mutter) (!Ella und ihr Vater) (!Herr und Frau Schulte)
Welches Grundstück würden die beiden kaufen? (!1) (!2) (!3) (4) (!5) (!6)
Bevor die Familien anfängt ihr Haus zu bauen, soll das Grundstück mit einem Bauzaun gesichert werden. Zur Vereinfachung kannst du dir vorstellen, dass der Zaun direkt auf den Grundstücksgrenzen aufgestellt wird.
Beantworte die Fragen und überprüfe!
Für welches Grundstück braucht man am wenigsten Zaun? (!1) (!2) (!3) (!4) (5) (!6)
Für welches Grundstück braucht man am meisten Zaun? (!1) (!2) (3) (!4) (!5) (!6)
Der Flächeninhalt einer ebenen Figur
Am Flächeninhalt einer Fläche erkennt man, wie groß die Fläche ist. Man kann den Flächeninhalt bestimmen, indem man die Fläche mit Einheitsquadraten, die eine bestimmte Größe haben, auslegt.
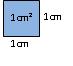
Ein Einheitsquadrat mit der Seitenlänge 1 cm hat den Flächeninhalt 1 cm2, man sagt "ein Quadratzentimeter":
Eine Fläche, die vollständig ausgelegt ist, indem man genau acht 1-cm2-Quadrate nebeneinanderlegt, hat den Flächeninhalt
A = 8 cm2.
Im folgenden Video wird das Prinzip an zwei Beispielen erklärt:
Schreibe das Grundwissen als Regelhefteintrag mit der Überschrift "Flächeninhalt" ab.
Ergänze bei deinem Eintrag die beiden Beispiele aus dem Video. Zeichne dazu die ursprünglichen Figuren ab und trage dort die Einheitsquadrate ein. Mache beim zweiten Beispiel farbig deutlich, welche beiden Flächen jeweils zusammen die Größe von einem Einheitsquadrat haben.