Flächeninhalt und Umfang/Flächeninhalt und Umfang eines Rechtecks berechnen: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 85: | Zeile 85: | ||
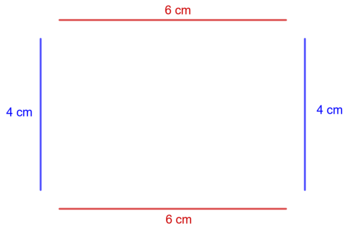
| Simon: || Bei der Umrandung des Rechtecks taucht genau zweimal die Länge auf und zweimal die Breite. Ich verdopple also zuerst die Länge und die Breite und addiere anschließend die beiden Produkte.|| [[Bild:UR2.png|350px]]|| Umfang = 2 ⋅ Länge + 2 ⋅ Breite || u = 2 ⋅ a + 2 ⋅ b | | Simon: || Bei der Umrandung des Rechtecks taucht genau zweimal die Länge auf und zweimal die Breite. Ich verdopple also zuerst die Länge und die Breite und addiere anschließend die beiden Produkte.|| [[Bild:UR2.png|350px]]|| Umfang = 2 ⋅ Länge + 2 ⋅ Breite || u = 2 ⋅ a + 2 ⋅ b | ||
|- | |- | ||
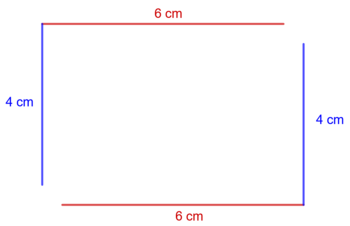
| Pauline || Den Weg um das Rechteck kann ich in zwei Hälften einteilen. Bei beiden Hälften muss ich einmal die Länge und einmal die Breite des Rechtecks berücksichtigen. Ich addiere also zuerst Länge und Breite und verdopple anschließend die Summe. || [[Bild:UR3.png|350px]] || Umfang = 2 ⋅ (Länge + Breite) || u = 2 ⋅ (a + b) | | Pauline: || Den Weg um das Rechteck kann ich in zwei Hälften einteilen. Bei beiden Hälften muss ich einmal die Länge und einmal die Breite des Rechtecks berücksichtigen. Ich addiere also zuerst Länge und Breite und verdopple anschließend die Summe. || [[Bild:UR3.png|350px]] || Umfang = 2 ⋅ (Länge + Breite) || u = 2 ⋅ (a + b) | ||
|} | |} | ||
</div> | </div> | ||
{{Box|1=Aufgabe 18|2=Berechne mithilfe der neuen Formeln, die Simon und Pauline verwendet haben, im folgenden Fenster den Umfang von mindestens 5 Rechtecken. | |||
<ggb_applet id="AyyJ8k2P" width="900" height="650" />|Üben}} | |||
=Sichern und Üben= | |||
Version vom 2. Mai 2020, 08:20 Uhr
Bei kleineren Flächen klappen das Auslegen mit Einheitsquadraten und das anschließende Auszählen dieser Quadrate noch ganz gut. Je größer die Flächen aber werden, desto aufwändiger wird dieses Verfahren. Beim Rechteck ist es aber möglich, den Flächeninhalt mithilfe einer einfachen Formel ohne die Verwendung von Einheitsquadraten auszurechnen.
Flächeninhalt des Rechtecks berechnen
Der Flächeninhalt eines Rechtecks hängt von der Länge a und der Breite b des Rechtecks ab. Zeichne die folgende Tabelle in dein Heft und fülle jede Zeile mithilfe einer neuen Aufgabe des interaktiven Fensters aus!
| Länge a | Breite b | Flächeninhalt A |
|---|---|---|

Sieh dir die Tabelle aus Aufgabe 1 genau an. Mit welcher Formel kann man den Flächeninhalt eines Rechtecks berechnen?
Mit Worten: (!Flächeninhalt = Länge + Breite) (Flächeninhalt = Länge ⋅ Breite) (!Flächeninhalt = Länge - Breite) (!Flächeninhalt = Länge : Breite) (!Flächeninhalt = Breite - Länge) (!Flächeninhalt = Breite : Länge)
Mit Formelzeichen: (!A = a + b) (A = a ⋅ b) (!A = a - b) (!A = a : b) (!A = b - a) (!a = b : A) (!a = A + b) (!a = A ⋅ b) (!a = A - b) (!a = b : A)
Berechne mithilfe der Formel den Flächeninhalt von mindestens 5 Rechtecken im folgenden Fenster:

Umfang des Rechtecks berechnen
Vielleicht fragst du dich gerade, warum hier noch einmal ein Abschnitt zum Umfang des Rechtecks kommt. Du hast ja bereits gelernt, wie man den Umfang beliebiger Vielecke berechnen kann. Bei manchen Flächen kann man die Berechnung des Umfangs jedoch mit einer Formel etwas abkürzen. Wie diese Abkürzung beim Rechteck aussehen kann, lernst du jetzt.
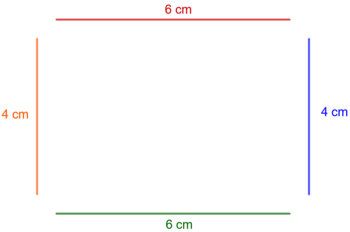
Kim, Simon und Pauline haben den Umfang des Rechtecks aus Aufgabe 16 auf verschiedenen Wegen berechnet:
Kim: u = 6 cm + 4 cm + 6 cm + 4cm = 10 cm + 6 cm + 4 cm = 16 cm + 4 cm = 20 cm
Simon: u = 2 ⋅ 6 cm + 2 ⋅ 4 cm = 12 cm + 8 cm = 20 cm
Pauline: u = 2 ⋅ (6 cm + 4 cm) = 2 ⋅ 10 cm = 20 cm
a) Welche der Rechnungen passt am besten zu deinem Lösungsweg?
Berechne mithilfe der neuen Formeln, die Simon und Pauline verwendet haben, im folgenden Fenster den Umfang von mindestens 5 Rechtecken.

Sichern und Üben