Flächeninhalt und Umfang/Flächeninhalt und Umfang eines Rechtecks berechnen: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (13 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 35: | Zeile 35: | ||
<ggb_applet id="tb5amkzy" width="900" height="650" />|3=Üben}} | <ggb_applet id="tb5amkzy" width="900" height="650" /> | ||
Folge dem folgenden Link, wenn das Fenster nicht richtig angezeigt wird: [https://www.geogebra.org/m/tb5amkzy https://www.geogebra.org/m/tb5amkzy]|3=Üben}} | |||
{{Box|1=Aufgabe 14|2=Sieh dir die Tabelle aus Aufgabe 1 genau an. Mit welcher Formel kann man den Flächeninhalt eines Rechtecks berechnen? | {{Box|1=Aufgabe 14|2=Sieh dir die Tabelle aus Aufgabe 1 genau an. Mit welcher Formel kann man den Flächeninhalt eines Rechtecks berechnen? | ||
| Zeile 48: | Zeile 50: | ||
|3=Üben}} | |3=Üben}} | ||
{{Box|1=Aufgabe 15|2=Berechne mithilfe der Formel den Flächeninhalt von mindestens 5 Rechtecken im folgenden Fenster: | |||
<ggb_applet id="MH6JeMyY" width="850" height="500" /> | |||
Folge dem folgenden Link, wenn das Fenster nicht richtig angezeigt wird: [https://www.geogebra.org/m/MH6JeMyY https://www.geogebra.org/m/MH6JeMyY]|3=Üben}} | |||
=Umfang des Rechtecks berechnen= | =Umfang des Rechtecks berechnen= | ||
Vielleicht fragst du dich gerade, warum hier noch einmal ein Abschnitt zum Umfang des Rechtecks kommt. Du hast ja bereits gelernt, wie man den Umfang beliebiger Vielecke berechnen kann. Bei manchen Flächen kann man die Berechnung des Umfangs jedoch mit einer Formel etwas abkürzen. Wie diese Abkürzung beim Rechteck aussehen kann, lernst du jetzt. | |||
{{Box|Aufgabe 16|Zeichne in dein Heft ein Rechteck mit der Länge 6 cm und der Breite 4 cm. Bestimme den Umfang dieses Rechtecks auf die Art und Weise, die du bereits kennengelernt hast.|Üben}} | |||
{{Box|1=Aufgabe 17|2=Kim, Simon und Pauline haben den Umfang des Rechtecks aus Aufgabe 16 auf verschiedenen Wegen berechnet: | |||
Kim: u = 6 cm + 4 cm + 6 cm + 4cm = 10 cm + 6 cm + 4 cm = 16 cm + 4 cm = 20 cm | |||
Simon: u = 2 ⋅ 6 cm + 2 ⋅ 4 cm = 12 cm + 8 cm = 20 cm | |||
Pauline: u = 2 ⋅ (6 cm + 4 cm) = 2 ⋅ 10 cm = 20 cm | |||
a) Welche der Rechnungen passt am besten zu deinem Lösungsweg? | |||
b) Ordne jedem der drei Kinder die passende Beschreibung der Vorgehensweise, die passende Skizze und die passenden Formeln zu. Wenn du alle Kärtchen zugeordnet hast, kannst du deine Lösung überprüfen. Fall dann wieder Kärtchen im unteren blauen Bereich landen, waren diese noch nicht richtig zugeordnet. | |||
|3=Üben}} | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
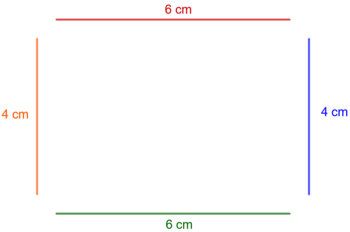
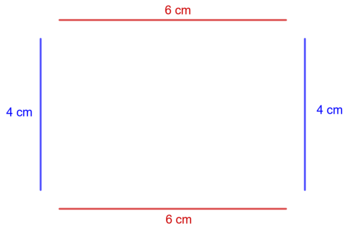
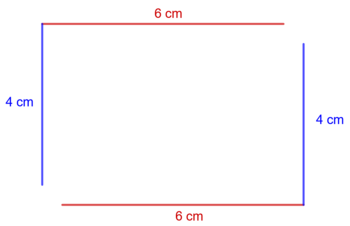
| Kim: || Ich gehe in Gedanken einmal um das Rechteck herum und addiere alle Längen, die ich dabei zurücklegen muss. || [[Bild:UR1.png|350px]] || Umfang = erste Seite + zweite Seite + dritte Seite + vierte Seite || u = a + b + c + d | |||
|- | |||
| Simon: || Bei der Umrandung des Rechtecks taucht genau zweimal die Länge auf und zweimal die Breite. Ich verdopple also zuerst die Länge und die Breite und addiere anschließend die beiden Produkte.|| [[Bild:UR2.png|350px]]|| Umfang = 2 ⋅ Länge + 2 ⋅ Breite || u = 2 ⋅ a + 2 ⋅ b | |||
|- | |||
| Pauline: || Den Weg um das Rechteck kann ich in zwei Hälften einteilen. Bei beiden Hälften muss ich einmal die Länge und einmal die Breite des Rechtecks berücksichtigen. Ich addiere also zuerst Länge und Breite und verdopple anschließend die Summe. || [[Bild:UR3.png|350px]] || Umfang = 2 ⋅ (Länge + Breite) || u = 2 ⋅ (a + b) | |||
|} | |||
</div> | |||
{{Box|1=Aufgabe 18|2=Berechne mithilfe der neuen Formeln, die Simon und Pauline verwendet haben, im folgenden Fenster den Umfang von mindestens 5 Rechtecken. | |||
<ggb_applet id="aepteukb" width="850" height="600" /> | |||
Folge dem folgenden Link, wenn das Fenster nicht richtig angezeigt wird: [https://www.geogebra.org/m/aepteukb https://www.geogebra.org/m/aepteukb]|3=Üben}} | |||
=Sichern und Üben= | |||
{{Box|Aufgabe 19|Erstelle einen Regelhefteintrag zu dem Wissen, das du auf dieser Seite gelernt hast. Der Eintrag soll Folgendes enthalten: | |||
* Alle neuen Formeln mit Worten und mit Formelzeichen | |||
* Zu jeder Formel eine Beispielrechnung| Üben}} | |||
{{Box|Aufgabe 20|Im folgenden Fenster findest du einige Übungen mit Umkehraufgaben zum Flächeninhalt und zum Umfang: | |||
<ggb_applet id="cfnr4mwf" width="900" height="600" /> | |||
Folge dem folgenden Link, wenn das Fenster nicht richtig angezeigt wird: [https://www.geogebra.org/m/cfnr4mwf https://www.geogebra.org/m/cfnr4mwf]|3=Üben}} | |||
{{Box|Aufgabe 21|Bearbeite Übungsaufgaben in deinem Mathebuch. Die folgenden Angaben beziehen sich auf ''Neue Wege 5 (NRW, G9, 2019)'': | |||
S. 183 Nr. 5 | |||
S. 183 Nr. 6 ''oder'' drei Teilaufgaben von S. 184 Nr. 7 ''(Wähle selbst)'' | |||
S. 184 Nr. 9|Üben}} | |||
| Zeile 68: | Zeile 136: | ||
[[Kategorie:Sekundarstufe 1]] | [[Kategorie:Sekundarstufe 1]] | ||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
[[Kategorie:Flächeninhalt]] | [[Kategorie:Flächeninhalt]] | ||
Aktuelle Version vom 29. März 2022, 22:36 Uhr
Bei kleineren Flächen klappen das Auslegen mit Einheitsquadraten und das anschließende Auszählen dieser Quadrate noch ganz gut. Je größer die Flächen aber werden, desto aufwändiger wird dieses Verfahren. Beim Rechteck ist es aber möglich, den Flächeninhalt mithilfe einer einfachen Formel ohne die Verwendung von Einheitsquadraten auszurechnen.
Flächeninhalt des Rechtecks berechnen
Der Flächeninhalt eines Rechtecks hängt von der Länge a und der Breite b des Rechtecks ab. Zeichne die folgende Tabelle in dein Heft und fülle jede Zeile mithilfe einer neuen Aufgabe des interaktiven Fensters aus!
| Länge a | Breite b | Flächeninhalt A |
|---|---|---|

Sieh dir die Tabelle aus Aufgabe 1 genau an. Mit welcher Formel kann man den Flächeninhalt eines Rechtecks berechnen?
Mit Worten: (!Flächeninhalt = Länge + Breite) (Flächeninhalt = Länge ⋅ Breite) (!Flächeninhalt = Länge - Breite) (!Flächeninhalt = Länge : Breite) (!Flächeninhalt = Breite - Länge) (!Flächeninhalt = Breite : Länge)
Mit Formelzeichen: (!A = a + b) (A = a ⋅ b) (!A = a - b) (!A = a : b) (!A = b - a) (!a = b : A) (!a = A + b) (!a = A ⋅ b) (!a = A - b) (!a = b : A)
Berechne mithilfe der Formel den Flächeninhalt von mindestens 5 Rechtecken im folgenden Fenster:

Umfang des Rechtecks berechnen
Vielleicht fragst du dich gerade, warum hier noch einmal ein Abschnitt zum Umfang des Rechtecks kommt. Du hast ja bereits gelernt, wie man den Umfang beliebiger Vielecke berechnen kann. Bei manchen Flächen kann man die Berechnung des Umfangs jedoch mit einer Formel etwas abkürzen. Wie diese Abkürzung beim Rechteck aussehen kann, lernst du jetzt.
Kim, Simon und Pauline haben den Umfang des Rechtecks aus Aufgabe 16 auf verschiedenen Wegen berechnet:
Kim: u = 6 cm + 4 cm + 6 cm + 4cm = 10 cm + 6 cm + 4 cm = 16 cm + 4 cm = 20 cm
Simon: u = 2 ⋅ 6 cm + 2 ⋅ 4 cm = 12 cm + 8 cm = 20 cm
Pauline: u = 2 ⋅ (6 cm + 4 cm) = 2 ⋅ 10 cm = 20 cm
a) Welche der Rechnungen passt am besten zu deinem Lösungsweg?
Berechne mithilfe der neuen Formeln, die Simon und Pauline verwendet haben, im folgenden Fenster den Umfang von mindestens 5 Rechtecken.

Sichern und Üben
Erstelle einen Regelhefteintrag zu dem Wissen, das du auf dieser Seite gelernt hast. Der Eintrag soll Folgendes enthalten:
- Alle neuen Formeln mit Worten und mit Formelzeichen
- Zu jeder Formel eine Beispielrechnung
Im folgenden Fenster findest du einige Übungen mit Umkehraufgaben zum Flächeninhalt und zum Umfang:

Bearbeite Übungsaufgaben in deinem Mathebuch. Die folgenden Angaben beziehen sich auf Neue Wege 5 (NRW, G9, 2019):
S. 183 Nr. 5
S. 183 Nr. 6 oder drei Teilaufgaben von S. 184 Nr. 7 (Wähle selbst)
S. 184 Nr. 9