Quadratische Funktionen/Kapitel 4: Der Graph der quadratischen Funktion "f(x) = ax²"

Der Graph der quadratischen Funktion "f(x)$=$ax²"

In diesem Lernpfad lernst du die quadratische Funktion mit dem Vorfaktor a kennen! Bearbeite den unten aufgeführten Lernpfad!

• Auswirkungen des Vorfaktors auf die Normalparabel für den positiven Parameter a
• Auswirkungen des Vorfaktors auf die Normalparabel für den negativen Parameter a
• Auswirkungen des Vorfaktors auf einen Blick
• Aufstellen der Funktionsgleichung
• Aufgaben zur quadratischen Funktion "f(x)$=$ax²"

Lernpfadgruppe

• Die quadratische Funktion stellt sich vor
• Die Scheitelpunktsform - f(x) = (x - x_s)² + y_s
• Die Normalform - f(x) = x² + bx + c
• Die modifizierte Normalparabel f(x)= ax²
• Die Scheitelpunktsform, die Normalform und der Parameter a

Mathematik-digital.de

In dieser Lerneinheit lernst du nun den letzten Parameter kennen, der die Parabel verändert. Dieser Parameter sorgt für eine Streckung, Stauchung und/oder eine Spiegelung der Parabel. Wie das genau funktioniert lernst du in den nächsten Stationen.

Aber nun erstmal zur Funktionsgleichung. Der Parameter a kommt als "Vorfaktor" dazu, wodurch die folgende Funktionsgleichung entsteht:

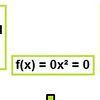
                         f(x)= a$\cdot$x2

Bevor wir uns mit den Auswirkungen des Vorfaktors beschäftigen, wollen wir die Begriffe "Streckung" und "Stauchung" kurz erläutern, damit jeder weiß, was damit gemeint ist.

Überlege dir, was du unter den Begriffen verstehst, und löse dann die folgende Aufgabe.

Streckung und Stauchung

Du hast verschiedene Bilder gegeben. Ordne die richtigen Begriffe zu!

gestreckt		gestaucht		normal

Nachdem wir das geklärt haben, können wir jetzt mit dem Lernpfad beginnen.

STATION 1: Auswirkungen des Vorfaktors auf die Normalparabel für den positiven Parameter a

Hinweise:

• In dem "GeoGebra-Applet" ist die Normalparabel schwarz eingezeichnet und die von a abhängige quadratische Funktion blau

• Bediene den roten Schieberegler mit der linken Maustaste, er verändert den Wert von a

Quadratische Funktion "f(x)$=$ax²" für positiven Parameter

Bediene den Schieberegler. Welche Veränderungen bewirkt der Vorfaktor a im Hinblick auf die Normalparabel?

Ordne die richtigen Begriffe zu:

Der Vorfaktor a führt zu einer Streckung oder Stauchung der Normalparabel in y-Richtung.
Es findet jedoch keine Streckung oder Stauchung statt, wenn der Wert von a Eins ist, denn dann ist "f(x) = 1x² = x²" identisch der Normalparabel.
Ist a > 1, so ist der Graph gestreckt.
Ist a < 1, so nennt man den Graph gestaucht.
Außerdem ist die quadratische Funktion "f(x) = ax²" für den positiven Vorfaktor a nach oben geöffnet und der Scheitelpunkt S ist tiefster Punkt mit den Koordinaten $(0 \vert 0)$.

Der Vorfaktor a (größer 0)

Für die quadratische Funktion "f(x)$=$ a$\cdot$x²" mit dem positiven Vorfaktor a gilt:

• Die von a abhängige Parabel entsteht aus der Normalparabel durch eine Streckung oder Stauchung in y-Richtung
• Für a $=$ 1 gilt: Identisch zur Normalparabel, denn "f(x)$=$ 1$\cdot$x²$=$ x²"
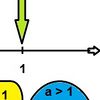
• Für a > 0 gilt:
  • Der Graph ist nach oben geöffnet
  • Scheitelpunkt S ist tiefster Punkt und liegt im Ursprung $S(0\!\,|\!\,0)$
  • Für a > 1 gilt: Der Graph ist gestreckt
  • Für a < 1 gilt: Der Graph ist gestaucht

Da wir den Fall für den positiven Vorfaktor a untersucht haben, schauen wir uns jetzt an, was passiert, wenn der Parameter a negativ wird.

STATION 2: Auswirkungen des Vorfaktors auf die Normalparabel für den negativen Parameter a

Bearbeite das folgende Quiz und lerne die Auswirkungen für den negativen Parameter a kennen.

Quadratische Funktion "f(x) = ax²" für negativen Parameter a

Bediene wieder den Schieberegler. Welche Veränderungen bewirkt der Vorfaktor a wenn er negativ wird?

Quiz:

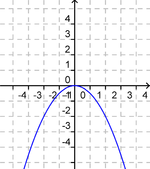
Wie ist die Parabel für a < 0 geöffnet? (!gar nicht) (!nach oben) (nach unten)

Welche Aussage ist für den negativen Vorfaktor a richtig? (!Es gibt keinen Scheitelpunkt) (!Der Scheitelpunkt S liegt im Ursprung und ist tiefster Punkt) (Der Scheitelpunkt S liegt im Ursprung und ist höchster Punkt)

Was bewirkt der negative Vorfaktor a? (!Er bewirkt nur eine Streckung) (!Er bewirkt nur eine Stauchung) (Er bewirkt eine Streckung oder Stauchung)

Was passiert wenn der Vorfaktor a = -1 ist? (Die Normalparabel wird an der x-Achse gespiegelt) (!Die Parabel ist nach oben geöffnet) (!Die Parabel ist gestaucht)

Für welche negativen Werte von a, ist die nach unten geöffnete Parabel, gestreckt? (!für a < -0,5) (!für a > -1) (für a < -1)

Für welche negativen Werte von a, ist die nach unten geöffnete Parabel, gestaucht? (!für a > -2) (für 0 > a > -1) (!für -2 < a < 0)

Der Parameter a < 0

Für die quadratische Funktion "f(x)$=$ a$\cdot$x²" mit dem negativen Vorfaktor a gilt:

• Die von a abhängige Parabel entsteht zum einen aus der Spiegelung an der x-Achse sowie einer Streckung oder Stauchung in y-Richtung
• Für a $=$ -1 gilt: An der x-Achse gespiegelte Normalparabel; "f(x)$=$-1$\cdot$x²$=$ -x²"
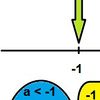
• Für a < 0 gilt:
  • Der Graph ist nach unten geöffnet
  • Scheitelpunkt S ist höchster Punkt und liegt im Ursprung $S(0\!\,|\!\,0)$
  • Für a < -1 gilt: Der Graph ist gestreckt
  • Für a > -1 gilt: Der Graph ist gestaucht

STATION 3: Auswirkungen des Vorfaktors auf einen Blick

Da das nun einige Eigenschaften sowohl für den positiven, als auch für den negativen Vorfaktor a sind, wollen wir diese mal zusammenfassen. Dabei soll dir die folgende Grafik helfen, welche du zunächst nur in einzelnen Puzzleteilen vorfindest. Löse das Puzzle, du wirst feststellen, es ist gar nicht so schwer!!

Versuche mit Hilfe der Grafik und deinem bisherigen Wissen, die richtigen Kombinationen zu finden!
Lies dafür zunächst alle Vorgaben und alle möglichen Lösungen genau durch.

	Vorgabe	Passender Textbaustein
1.	Vorfaktor a ist negativ	Nach unten geöffnete Parabel
2.	a < -1	Graph ist gestreckt
3.	Scheitelpunkt S für negativen Parameter a	Scheitelpunkt ist höchster Punkt und liegt im Ursprung S $[0|0]$
4.	0 > a > -1	Graph ist gestaucht
5.	Vorfaktor a ist positiv	Nach oben geöffnete Parabel
6.	0 < a < 1	Graph ist gestaucht
7.	Scheitelpunkt S für positiven Parameter a	Scheitelpunkt ist tiefster Punkt und liegt im Ursprung S $[0|0]$
8.	a > 1	Graph ist gestreckt
9.	Der Vorfaktor a bewirkt eine…	Streckung oder Stauchung der Normalparabel

STATION 4: Aufstellen der Funktionsgleichung

Bisher konntest du den Wert des Vorfaktors a am Schieberegler des "GeoGebra-Applets" ablesen. Nun wollen wir lernen, wie man anhand des Graphen, den Parameter a bestimmt. Wir betrachten in diesem Lernpfad den Spezialfall für "f(x)= a$\cdot$x²". Im nächsten Lernpfad erfährst du dann, wie man den Parameter a auch für verschobene Parabeln bestimmt.

Bearbeite die folgende Aufgabe und versuche dabei die Vorgehensweise, zum Bestimmen des Parameters a, zu erkennen.

Quadratische Funktion "f(x) = ax²" mit positivem und negativem Parameter a

1. Gegeben ist die Funktion "f(x) = 1x²". Gehe vom Scheitelpunkt aus auf der x-Achse eine Einheit nach rechts.

Wie viele Einheiten musst du dann in y-Richtung gehen, um die Parabelkurve zu erreichen? (!2) (1) (!3)

2. Bediene nun den Schieberegler und stelle a = 2 ein. Gehe genauso vor wie in der Aufgabe 1. Gehe vom Scheitelpunkt aus eine Einheit nach rechts auf der x-Achse.

Um wie viele Einheiten muss du nun in y-Richtung gehen? (!3) (2) (!4)

3. Erkennst du schon ein Muster? Versuche das folgende Quiz zu lösen:

Wenn man vom Scheitelpunkt aus eine Einheit nach rechts und 4 Einheiten nach oben geht, dann hat der Parameter a den Wert: (!1) (!2) (!3) (4)

4. Stelle nun den Schieberegler auf den Wert a = -2.

Funktioniert das Ablesen bei einem negativen Vorfaktor a genauso wie bei positiven Werten von a? (!Nein) (JA)

5. Man geht vom Scheitelpunkt aus eine Einheit nach rechts und drei Einheiten nach unten!

Wie lautet der Wert vom Vorfaktor a?? (!1) (-3) (!3)

Bestimmung des Parameters a

Anleitung zur Bestimmung des Vorfaktors a:

• Der Startpunkt zum Bestimmen des Vorfaktors ist der Scheitelpunkt
  
• Gehe auf der x-Achse eine Einheit nach rechts
  
• Bestimme in y-Richtung die Anzahl der Einheiten bis zur Parabelkurve
  
• Die Anzahl der Einheiten ergibt den Wert vom Vorfaktor a
  
• Hat man die Einheiten nach oben abgezählt, so ist der Wert von a positiv
  
• Hat man die Einheiten nach unten abgezählt, so ist der Wert von a negativ
  

Um zu überprüfen, ob du die Vorgehensweise zum Finden des Vorfaktors a verstanden hast, versuche die nächste Aufgabe zu lösen.

Bestimme die Funktionsgleichung wie gerade erlernt!

Ordne Bilder und Funktionsgleichungen richtig zu!

y = -0,5x2		y = 0x2		y = 2x2		y = -4x2		y = 0,5x2

STATION 5: Aufgaben zur quadratischen Funktion "f(x)$=$ax²"

Parabeln im Alltag

Die Parabelform taucht auch in Bereichen des Alltags auf. Hier siehst du den Ausschnitt einer parabelförmigen Brückenaufhängung (Die Hohenzollernbrücke über der Rhein bei Köln). Beantworte zuerst die folgende Frage und stelle dann den Graph durch Bedienen des Schiebereglers richtig ein!

Frage:

Was muss für den Vorfaktor a gelten? (Mehrere Antworten möglich!) (!er ist positiv) (er ist negativ) (!a < -1) (-1 < a < 0)

Wir betrachten die Funktion f(x) = 0,5x²

Gegeben ist die Funktionsvorschrift "f(x) = 0,5x²".

Im folgenden "GeoGebra-Applet" erkennst du die Punkte A, B, C und D. Diese Punkte können in y-Richtung verschoben werden. Ihr x-Wert hingegen ist fest vorgegeben. Überlege dir, welchen Wert der jeweilige y-Wert einnehmen muss und bewege den entsprechenden Punkt an diese Stelle. Überprüfe anschließend durch Anklicken des Kontrollkästchens "Graph", ob all deine Punkte auf dem Graph liegen. Liegen alle Punkte auf dem Graph, dann hast du die Aufgabe richtig gelöst!

Bestimme den Parameter a

Gegeben ist die quadratische Funktion "f(x) = ax²".

Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt $[2|12]$ verläuft? (!1) (!2) (3) (!4)

Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt $[3|9]$ verläuft? (1) (!2) (!3) (!4)

Welchen Wert hat der Parameter a, wenn der Graph durch den Punkt $[4|32]$ verläuft? (!1) (2) (!3) (!4)

Glückwunsch!

Damit hast du den Lernpfad "Der Graph der quadratischen Funktion f(x)$=$ax²" abgeschlossen. Im folgenden und letzten Lernpfad werden schließlich alle Parameter und Darstellungsformen der quadratischen Funktion gemeinsam betrachtet und geübt. Viel Spaß!

Die Normalform, die Scheitelpunktsform und der Parameter a