Beschreibende Statistik/Grundbegriffe: Unterschied zwischen den Versionen
main>Nina Krämer Keine Bearbeitungszusammenfassung |
K (23 Versionen importiert) |
||
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Aufgabe|Los geht's mit den '''Grundbegriffen der beschreibenden Statistik'''. Zunächst gibt es eine Übersicht über alles, was Sie im ersten Kapitel erwartet. | |||
}} | |||
[[Datei: | * [[Beschreibende Statistik/Grundgesamtheit, Stichprobe und Stichprobenumfang|Grundgesamtheit, Stichprobe und Stichprobenumfang]] | ||
* [[Beschreibende Statistik/Merkmal und Merkmalsausprägungen|Merkmal und Merkmalsausprägungen]] | |||
* [[Beschreibende Statistik/Qualitative und Quantitative Merkmale, Skalen|Qualitative und Quantitative Merkmale, Skalen]] | |||
* [[Beschreibende Statistik/Absolute und Relative Häufigkeiten|Absolute und Relative Häufigkeiten]] | |||
* [[Beschreibende Statistik/Klassenbildung|Klassenbildung]] | |||
** [[Beschreibende Statistik/Klassenbildung/Klassen mit gleicher Klassenbreite|Klassen mit gleicher Klassenbreite]] | |||
** [[Beschreibende Statistik/Klassenbildung/Klassen mit unterschiedlicher Klassenbreite|Klassen mit unterschiedlicher Klassenbreite]] | |||
== Befragung == | |||
[[Datei:Umfrage Eisdiele Urliste.PNG|rechts|Einführung Merkmale und Merkmalsausprägungen]] | |||
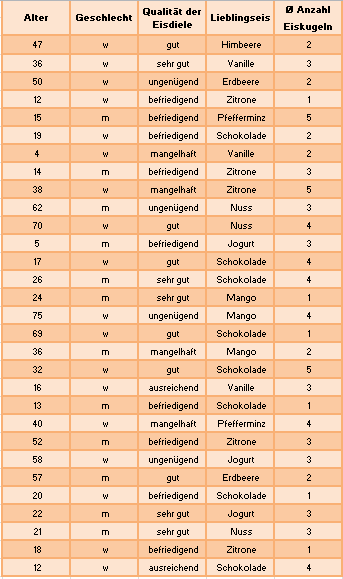
Die Grundlage einer jeden statistischen Erhebung ist die '''Befragung''' oder Untersuchung. Die Beobachtungswerte werden in einer '''Urliste''' gesammelt und sind zunächst recht unübersichtlich. Hier lernen Sie zunächst die Aufbereitung der Daten als '''Häufigkeitsverteilung''' schrittweise kennen und nutzen. | |||
<!-- Einführungsbeispiel Teil 1 --> | |||
'''Einführungsbeispiel - Umfrage''' | |||
Die Eisdiele „Rabe“ in Hattingen hat im Mai 2014 unter ihren Kunden eine Umfrage zur Verbesserung ihres Angebots gemacht. Hierzu wurden stichprobenartig 30 Kunden befragt. | |||
Das Ergebnis der Umfrage liegt als ungeordnete Liste (siehe Tabelle rechts) vor. Auf den ersten Blick lässt sich kein Ergebnis erkennen, welches zur Verbesserung des Angebots der Eisdiele führen könnte. Also müssen die erhobenen Daten so aufbereitet werden, dass sich eine Aussage ablesen lässt. Die verschiedenen Möglichkeiten zur Aufbereitung der vorliegenden Daten wird an diesem Beispiel schrittweise durchgeführt. Die dazu benötigten Grundbegriffe werden eingeführt. | |||
{{clear}} | |||
== Merksätze == | |||
{{Aufgabe| | |||
Herzlichen Glückwunsch! Sie haben das erste Kapitel erfolgreich abgeschlossen. | |||
Ihr Regelheft enthält schon viele Informationen. Überprüfen Sie, ob Sie alles notiert haben.; | |||
}} | |||
;Regelheft | |||
<!-- Merke-Grundgesamtheit, Stichprobe und Stichprobenumfang --> | |||
{{Merke||1= | |||
Eine <span style="background:yellow">'''Grundgesamtheit'''</span> ist die Menge aller möglichen Objekte, über die man eine Aussage machen möchte. | |||
Die Grundgesamtheit kann | |||
: - begrenzt (z. B. alle Schüler der Klasse HHU5 des Berufskollegs Hattingen), | |||
: - sehr groß (z. B. alle Einwohner Deutschlands im Jahr 2014) oder | |||
: - unbegrenzt sein. | |||
Eine <span style="background:yellow">'''Stichprobe'''</span> ist eine Teilmenge der Grundgesamtheit; ihre Größe ist immer begrenzt. | |||
Der <span style="background:yellow">'''Stichprobenumfang <math>n</math>'''</span> gibt die Größe der Stichprobe an. | |||
}} | |||
<!-- Ende Merke-Grundgesamtheit, Stichprobe und Stichprobenumfang --> | |||
<!-- Merksatz Merkmal, Beobachtungswert, Urliste, Merkmalsausprägungen, Merkmalsträger --> | |||
{{Merke|1= | |||
Jede in einer statistischen Erhebung untersuchte Frage heißt <span style="background:yellow">'''Merkmal'''</span>. | |||
Die einzelnen Antworten heißen <span style="background:yellow">'''Beobachtungswerte'''</span> und werden getrennt nach Merkmalen in einer <span style="background:yellow">'''Urliste'''</span> festgehalten. Die Beobachtungswerte werden mit <math>a_i</math> bezeichnet. | |||
Die Anzahl aller Beobachtungswerte <math>a_i</math> ist gleich dem Stichprobenumfang <math>n</math>. | |||
Zu einer Stichprobe vom Umfang <math>n</math> gibt es in der zugehörigen Urliste die Beobachtungswerte <math>a_1; a_2;...;a_{n-1};a_n</math>. | |||
Die verschiedenen Werte die ein Merkmal annimmt, werden <span style="background:yellow">'''Merkmalsausprägungen'''</span> genannt und mit <math>x_i</math> bezeichnet. Es kann höchstens so viele Merkmalsausprägungen geben, wie es Beobachtungswerte in der Urliste gibt. In der Regel wird die Anzahl <math>k</math> der Merkmalsausprägungen kleiner sein als der Stichprobenumfang. | |||
Die zu einem Merkmal gehörenden Ausprägungen werden mit <math>x_1;x_2;...;x_{k-1};x_k</math> bezeichnet. | |||
Jedes Element der Stichprobe einer statistischen Erhebung ist ein <span style="background:yellow">'''Merkmalsträger'''</span> bezogen auf die untersuchten Merkmale. | |||
}} | |||
<!-- Ende Merksatz Merkmal, Beobachtungswert, Urliste, Merkmalsausprägungen, Merkmalsträger --> | |||
<!-- Merke Merkmalsausprägungen --> | |||
{{Merke|1= | |||
Man unterscheidet in | |||
* <span style="background:yellow">quantitative Merkmale</span>, deren Merkmalsausprägungen aus Zahlen oder Größenwerten bestehen | |||
** mit <span style="background:yellow">metrisch diskreter Skala</span> (nur ganze Zahlen) | |||
** mit <span style="background:yellow">metrisch stetiger Skala</span> (alle Kommazahlen) | |||
* <span style="background:yellow">qualitative Merkmale</span>, deren Merkmalausprägungen in Textform oder als Zahlwerte (ohne mögliche sinnvolle Rechenoperationen) gegeben sind | |||
** mit <span style="background:yellow">Ordinalskala</span> (die Merkmalsausprägungen lassen sich in eine natürliche Reihenfolge bringen) | |||
** mit <span style="background:yellow">Nominalskala</span> (die Merkmalsausprägungen haben keine Wertigkeit) | |||
}} | |||
<!-- Ende Merke Merkmalsausprägungen --> | |||
<!-- Definition absolute und relative Häufigkeiten --> | |||
{{Merke|1= | |||
Die <span style="background:yellow">'''absolute Häufigkeit'''</span> <math>H(x_i)</math> gibt die Anzahl aller Merkmalsträger mit dieser Merkmalsausprägung <math>x_i</math> an. | |||
Statt <math>H(x_i)</math> schreibt man auch kurz <math>H_i</math>. | |||
Die <span style="background:yellow">'''relative Häufigkeit'''</span> <math>h(x_i)=\frac{H(x_i)} {n}</math> gibt den Anteil aller Merkmalsträger mit dieser Merkmalsausprägung <math>x_i</math> bezogen auf den Stichprobenumfang <math>n</math> an. | |||
Statt <math>h(x_i)</math> schreibt man auch kurz <math>h_i</math>. | |||
}} | |||
<!-- Ende Definition absolute und relative Häufigkeiten --> | |||
<!-- Merksatz absolute und relative Häufigkeiten --> | |||
{{Merke|1= | |||
Die Summe der absoluten Häufigkeiten ist immer gleich der Anzahl aller Merkmalsträger, also gleich dem Stichprobenumfang. | |||
Mathematische Kurzschreibweise: | |||
:: <math>\sum_{i=1}^k H(x_i)=n</math> oder noch kürzer <math>\sum_{i=1}^k H_i=n</math>, | |||
wobei <math>k</math> die Anzahl der Merkmalsausprägungen und <math>n</math> den Stichprobenumfang bezeichnen. | |||
Eine Darstellung der Merkmalsausprägungen mit absoluten Häufigkeiten nennt man <span style="background:yellow">'''absolute Häufigkeitsverteilung'''</span>. | |||
Die Summe der relativen Häufigkeiten ist immer gleich 1, also 100 %. | |||
Mathematische Kurzschreibweise: | |||
:: <math>\sum_{i=1}^k h(x_i)=1</math> oder noch kürzer <math>\sum_{i=1}^k h_i=1</math>, | |||
wobei <math>k</math> die Anzahl der Merkmalsausprägungen und <math>n</math> den Stichprobenumfang bezeichnen. | |||
Eine Darstellung der Merkmalsausprägungen mit relativen Häufigkeiten nennt man <span style="background:yellow">'''relative Häufigkeitsverteilung'''</span>. | |||
}} | |||
<!-- Ende Merksatz absolute und relative Häufigkeiten --> | |||
<!-- Merke Klassen --> | |||
{{Merke|1= | |||
Wenn bei einer umfangreichen Stichprobe sehr viele unterschiedliche Merkmalsausprägungen auftreten, so bietet es sich an, ähnliche Werte in sogenannte <span style="background:yellow">'''Klassen <math>k_i</math>'''</span> der <span style="background:yellow">(Klassen-)Breite <math>b_i</math></span> zusammenzufassen. | |||
}} | |||
<!-- Ende Merke Klassen --> | |||
<!-- Merke Klassen,Klassenanzahl, Spannweite, Klassenbreite --> | |||
{{Merke|1= | |||
Die einzelnen <span style="background:yellow">Klassen</span> bezeichnet man mit <math>k_i</math>, wobei <math>i=</math> <math>1;2;\dots;k-1;k</math> gilt. | |||
<span style="background:yellow">Klassenanzahl</span>: | |||
:: <math>k \approx \sqrt{n}</math> | |||
<span style="background:yellow">Spannweite</span>: | |||
:: <math>R= x_{max}-x_{min}</math> | |||
<span style="background:yellow">Klassenbreite</span>: | |||
:: <math>b=\frac{Spannweite}{Anzahl der Klassen}=\frac{R}{k}</math> | |||
}} | |||
<!-- Ende Merke Klassenanzahl, Spannweite, Klassenbreite --> | |||
<!-- Merke Klassen --> | |||
{{Merke|1= | |||
Bei Klassen mit unterschiedlichen Breiten ist jeder Klasse <math>k_i</math> ihre Breite <math>b_i</math> zuzuordnen | |||
Vorsicht bei Statistiken mit unterschiedlich breiten Klassen. Hier weiß man nie, was der Autor verstecken will. | |||
}} | |||
<!-- Ende Merke Klassen --> | |||
{{clear}} | |||
{{Fortsetzung|weiter=Grundgesamtheit, Stichprobe und Stichprobenumfang|weiterlink=Beschreibende Statistik/Grundgesamtheit, Stichprobe und Stichprobenumfang}} | |||
{{Beschreibende Statistik}} | |||
Aktuelle Version vom 15. April 2019, 10:39 Uhr
Los geht's mit den Grundbegriffen der beschreibenden Statistik. Zunächst gibt es eine Übersicht über alles, was Sie im ersten Kapitel erwartet.
- Grundgesamtheit, Stichprobe und Stichprobenumfang
- Merkmal und Merkmalsausprägungen
- Qualitative und Quantitative Merkmale, Skalen
- Absolute und Relative Häufigkeiten
- Klassenbildung
Befragung
Die Grundlage einer jeden statistischen Erhebung ist die Befragung oder Untersuchung. Die Beobachtungswerte werden in einer Urliste gesammelt und sind zunächst recht unübersichtlich. Hier lernen Sie zunächst die Aufbereitung der Daten als Häufigkeitsverteilung schrittweise kennen und nutzen.
Einführungsbeispiel - Umfrage
Die Eisdiele „Rabe“ in Hattingen hat im Mai 2014 unter ihren Kunden eine Umfrage zur Verbesserung ihres Angebots gemacht. Hierzu wurden stichprobenartig 30 Kunden befragt.
Das Ergebnis der Umfrage liegt als ungeordnete Liste (siehe Tabelle rechts) vor. Auf den ersten Blick lässt sich kein Ergebnis erkennen, welches zur Verbesserung des Angebots der Eisdiele führen könnte. Also müssen die erhobenen Daten so aufbereitet werden, dass sich eine Aussage ablesen lässt. Die verschiedenen Möglichkeiten zur Aufbereitung der vorliegenden Daten wird an diesem Beispiel schrittweise durchgeführt. Die dazu benötigten Grundbegriffe werden eingeführt.
Merksätze
Herzlichen Glückwunsch! Sie haben das erste Kapitel erfolgreich abgeschlossen.
Ihr Regelheft enthält schon viele Informationen. Überprüfen Sie, ob Sie alles notiert haben.;
- Regelheft
Eine Grundgesamtheit ist die Menge aller möglichen Objekte, über die man eine Aussage machen möchte.
Die Grundgesamtheit kann
- - begrenzt (z. B. alle Schüler der Klasse HHU5 des Berufskollegs Hattingen),
- - sehr groß (z. B. alle Einwohner Deutschlands im Jahr 2014) oder
- - unbegrenzt sein.
Eine Stichprobe ist eine Teilmenge der Grundgesamtheit; ihre Größe ist immer begrenzt.
Der Stichprobenumfang gibt die Größe der Stichprobe an.
Jede in einer statistischen Erhebung untersuchte Frage heißt Merkmal.
Die einzelnen Antworten heißen Beobachtungswerte und werden getrennt nach Merkmalen in einer Urliste festgehalten. Die Beobachtungswerte werden mit bezeichnet.
Die Anzahl aller Beobachtungswerte ist gleich dem Stichprobenumfang .
Zu einer Stichprobe vom Umfang gibt es in der zugehörigen Urliste die Beobachtungswerte .
Die verschiedenen Werte die ein Merkmal annimmt, werden Merkmalsausprägungen genannt und mit bezeichnet. Es kann höchstens so viele Merkmalsausprägungen geben, wie es Beobachtungswerte in der Urliste gibt. In der Regel wird die Anzahl der Merkmalsausprägungen kleiner sein als der Stichprobenumfang. Die zu einem Merkmal gehörenden Ausprägungen werden mit bezeichnet.
Jedes Element der Stichprobe einer statistischen Erhebung ist ein Merkmalsträger bezogen auf die untersuchten Merkmale.
Man unterscheidet in
- quantitative Merkmale, deren Merkmalsausprägungen aus Zahlen oder Größenwerten bestehen
- mit metrisch diskreter Skala (nur ganze Zahlen)
- mit metrisch stetiger Skala (alle Kommazahlen)
- qualitative Merkmale, deren Merkmalausprägungen in Textform oder als Zahlwerte (ohne mögliche sinnvolle Rechenoperationen) gegeben sind
- mit Ordinalskala (die Merkmalsausprägungen lassen sich in eine natürliche Reihenfolge bringen)
- mit Nominalskala (die Merkmalsausprägungen haben keine Wertigkeit)
Die absolute Häufigkeit gibt die Anzahl aller Merkmalsträger mit dieser Merkmalsausprägung an.
Statt schreibt man auch kurz .
Die relative Häufigkeit gibt den Anteil aller Merkmalsträger mit dieser Merkmalsausprägung bezogen auf den Stichprobenumfang an.
Statt schreibt man auch kurz .
Die Summe der absoluten Häufigkeiten ist immer gleich der Anzahl aller Merkmalsträger, also gleich dem Stichprobenumfang.
Mathematische Kurzschreibweise:
- oder noch kürzer ,
wobei die Anzahl der Merkmalsausprägungen und den Stichprobenumfang bezeichnen.
Eine Darstellung der Merkmalsausprägungen mit absoluten Häufigkeiten nennt man absolute Häufigkeitsverteilung.
Die Summe der relativen Häufigkeiten ist immer gleich 1, also 100 %.
Mathematische Kurzschreibweise:
- oder noch kürzer ,
wobei die Anzahl der Merkmalsausprägungen und den Stichprobenumfang bezeichnen.
Eine Darstellung der Merkmalsausprägungen mit relativen Häufigkeiten nennt man relative Häufigkeitsverteilung.
Die einzelnen Klassen bezeichnet man mit , wobei gilt.
Klassenanzahl:
Spannweite:
Klassenbreite:
Bei Klassen mit unterschiedlichen Breiten ist jeder Klasse ihre Breite zuzuordnen
Vorsicht bei Statistiken mit unterschiedlich breiten Klassen. Hier weiß man nie, was der Autor verstecken will.
Lernpfad Beschreibende Statistik
- Grundbegriffe
- Graphische Darstellungen von Häufigkeitsverteilungen
- Lagemaße
(arithmetisches Mittel, Modus, Median) - Streuungsmaße
(mittlere absolute Abweichung, mittlere quadratische Abweichung, Standardabweichung) - Einsatz des Taschenrechners
(Bedienung Casio fx-991DE PLUS)