Wiederholung (proportionale) Zuordnungen

Inhaltsverzeichnis

1. Startseite
2. Wiederholung (proportionale) Zuordnungen
3. Funktion als eindeutige Zuordnung
4. Lineare Funktionen

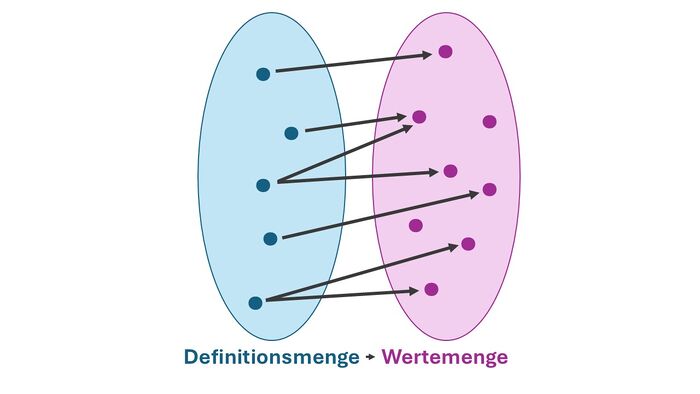
Was ist überhaupt eine "Zuordnung"?

Im Alltag gibt es viele Situationen, in denen zwei Größen zusammenhängen.

Eine Größe nennen wir Eingangswert (Wert aus der Definitionsmenge), die andere Ausgangswert (Wert aus der Wertemenge).

Die blauen Punkte sind hier Werte aus der Definitionsmenge und die lila Punkte sind Werte aus der Wertemenge. Die Werte aus der Definitionsmenge werden der Wertemenge zugeordnet.

Definitions- und Wertebereich

Immer wenn jedem Wert aus dem Definitionsbereich mindestens ein Wert aus dem Wertebereich zugeordnet wird, sprechen wir von einer Zuordnung. Zusammengehörige Werte nennen wir Wertepaare.

Das kann so aussehen:

Beispiel

Wenn ein Zug 120 km pro Stunde fährt, hängt die gefahrene Strecke davon ab, wie viel Zeit vergangen ist. Man sagt, der Zeit wird die gefahrene Strecke zugeordnet. In Symbolen schreibt man:

• Zeit → Strecke.

Weitere Beispiele sind:

1. Anzahl 🠒 Preis ("Die Anzahl wir dem Preis zugeordnet.")
2. Weg 🠒 Zeit ("Dem Weg wird die Zeit zugeordnet.")
3. Klasse 🠒 Schüler:innen ("Der Klasse werden Schüler:innen zugeordnet.")
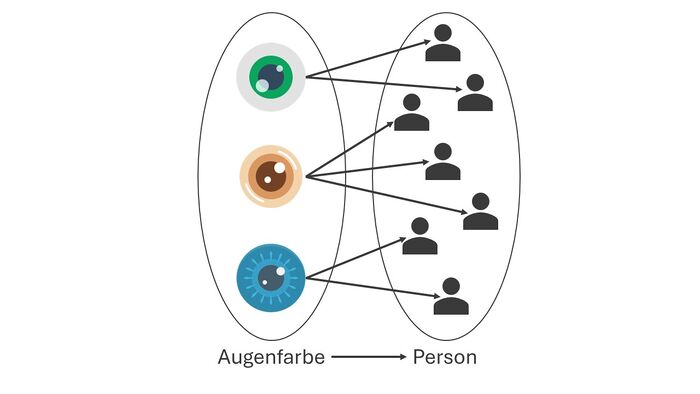
4. Augenfarbe 🠒 Person ("Die Augenfarbe wird Personen zugeordnet.")

eindeutige Zuordnung

Wird jedem Wert aus der Definitionsmenge genau ein Wert aus der Wertemenge zugeordnet, dann sprechen wir von einer eindeutigen Zuordnung.

Das bedeutet:

• Zu jedem x gehört genau ein y

Nie mehr oder weniger!

Zu jedem Wert aus der Definitionsmenge wird genau ein Wert aus der Wertemenge zugeordnet.

Beispiele

• 1 T-Shirt 🠒 12 €
• 2 T-Shirts 🠒 24 €
• 3 T-Shirts 🠒 36 €

Hier hat jeder Wert der Definitionsmenge (1, 2, 3) genau einen Ausgangswert (12, 24, 36).

Tier 🠒 Lebensraum ("Die Tiere werden dem jeweiligen Lebensraum zugeordnet.")

Das sind eindeutige Zuordnungen.

Gegenbeispiel

• 1 wird einmal 5 und 7 zugeordnet

Hier ist nicht klar, was "1" bedeutet, die Zuordnung ist dadurch nicht eindeutig!

Was macht eine Zuordnung "proportional"?

Eine Zuordnung heißt proportional, wenn Folgendes gilt:

Verändert man die eine Größe, verändert sich die andere im gleichen Verhältnis.

• Kurz: Je mehr von A, desto gleichmäßig mehr von B

Beispiel

• Doppelte Anzahl 🠒 doppelter Preis
• Dreifache Zeit 🠒 dreifache Strecke
• Halbe Anzahl 🠒 halber Preis

Möchte Tim kein Eis kaufen, dann muss er auch kein Geld zahlen.
Möchte Tim ein Eis kaufen, dann muss er 2 € zahlen.
Möchte Tim zwei Eis kaufen, dann muss er 4 € zahlen.

Proportionale Zuordnung

In einer proportionalen Zuordnung gilt immer:

y = k ⋅ x

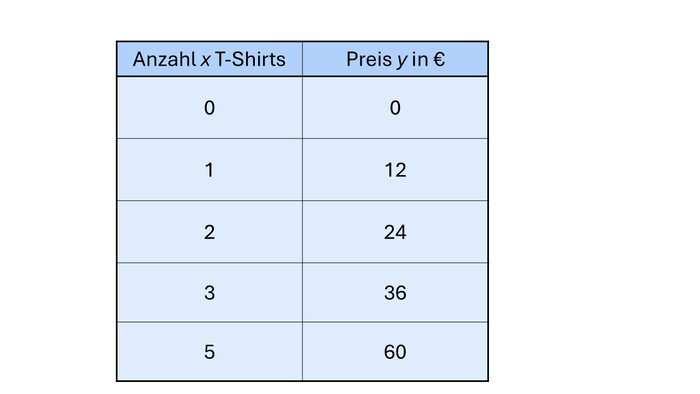
• x = Eingangswert (z.B. Anzahl an T-Shirts)
• y = Ausgangswert (z.B. Preis)
• k = Proportionalitätsfaktor
  • "Wie viel kostet ein Stück"
  • "Wie viel km schafft man in einer Stunde"
    

Es gibt also immer denselben Zuwachs pro Einheit, alle Wertepaare haben das gleiche Verhältnis. Dieses Verhältnis nennt man den Proportionalitätsfaktor k.

Beispiele für Proportionalitätsfaktoren:

• Preis pro Stück
• Strecke pro Zeit
• Geschwindigkeit in Kilometer pro Stunde (km/h)
• Verbrauch pro km
• Gewicht pro Stück (z.B. 1 Apfel = 150 g)

Konkretes Beispiel

• Verdoppelt man die Anzahl von 1 auf 2, so verdoppelt sich der Preis auch von 12 € auf 24 €.
• Verdreifacht man die Anzahl von 1 auf 3, so verdreifacht sich der Preis auch von 12 € auf 36 €.
• Aber das Verhältnis der Wertepaare bleibt immer gleich! Das kann man mit folgender Rechnung zeigen:

$\frac{Preis\, y\, in\, €}{Anzahl\, x\, T\, Shirts}=\frac{y}{x}=\frac{12}{1}=\frac{24}{2}=⋯=12=k$

Wie erkenne ich proportionale Zuordnungen?

In einer Tabelle

Eine Zuordnung ist proportional, wenn:

1. Das Verhältnis $\frac{y}{x}$ immer gleich bleibt
2. Die Wertepaare sich direkt "hochrechnen" lassen (Wenn x sich verdoppelt, dann verdoppelt sich auch y; Wenn sich x verdoppelt, dann verdreifacht sich auch y; etc.)

Beispiel - NICHT proportional

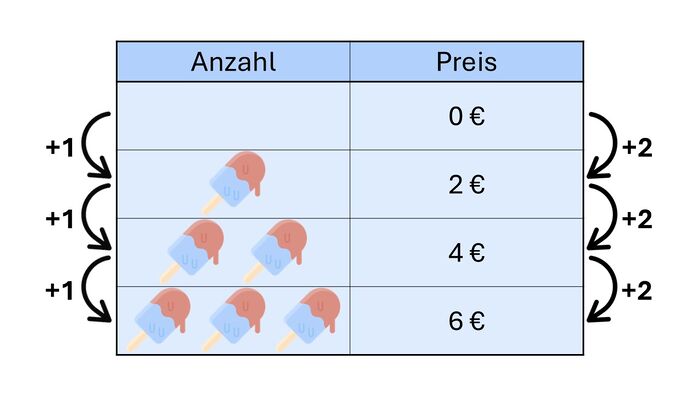
Warum ist diese Zuordnung denn nicht proportional? Schauen wir uns dieses Beispiel Mal genauer an:
Wenn man sich die linke Spalte dieser Tabelle ansieht, fällt auf, dass x immer um 1 steigt.
Wenn man sich aber die rechte Spalte anguckt, fällt auf, dass y bei dem ersten Mal um 5 steigt, aber dann beim zweiten Mal um 7 steigt, also ist der Proportionalitätsfaktor k nicht gleich:
$\frac{5}{1} = 5$
$\frac{10}{2} = 5$
ABER!

$\frac{17}{3} \neq 5$

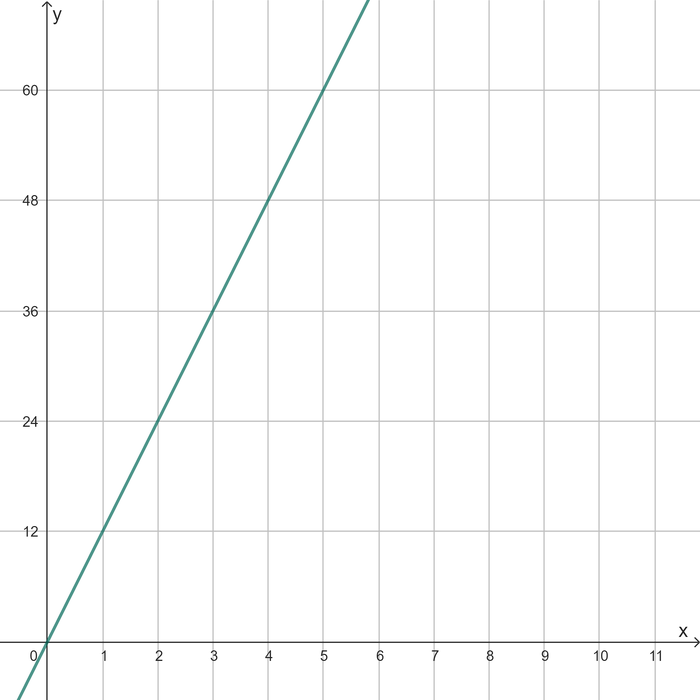
In einem Graphen (Koordinatensystem)

Eine proportionale Zuordnung hat immer folgende Eigenschaften:

• Es ist eine Gerade
• die durch den Ursprung (0|0) geht

Beispiel

Warum geht diese Gerade durch den Ursprung?

• Wenn du 0 T-Shirts kaufst, kostet das 0 €.
• Wenn du 0 Minuten mit dem Fahrrad gefahren bist, hast du 0 km zurückgelegt.

In einem Graphen (Koordinatensystem)

Wenn eine Zuordnung proportional ist, kannst du folgende Formel nutzen:
$y=k \cdot x$

(Diese Formel kennst du schon aus dem Kasten "Proportionale Zuordnung") Dann kannst du mit dieser Formel einen Graphen erstellen.

Aufgabe

Benutze den Schieberegler und beschreibe jeweils in einem kurzen Satz, wie der Graph bei den Werten $k = -2,3; k = 0; k = 1$ und $k = 5$ aussieht!
Achte dabei vor allem darauf, durch welche Punkte die Gerade, beziehungsweise der Graph, geht.

Beschreibe in welche Richtung der Graph steigt.

Typische Beispiele aus dem Alltag

Proportional

• Eis kostet 1,20 € pro Kugel.
• Beim Joggen läufst du 8 km pro Stunde.
• Eine Maschine produziert 50 Teile pro Stunde.
• Eine Kerze brennt jede Stunde 3 cm ab.

Nicht proportional

• Taxi: Grundgebühr + Preis pro km
• Busfahrkarte: kostet für Kinder weniger
• Handyvertrag: fester Grundpreis + Kosten pro GB
• Parkhaus: 1 € für die erste Stunde; jede weitere halbe Stunde kostet 50 ct.

Diese Situationen starten nicht bei 0! Das bringt uns nämlich zum nächsten Kapitel: Funktionen als eindeutige Zuordnungen, welche nicht durch 0 gehen müssen.

Startseite

Startseite

Funktionen als eindeutige Zuordnungen