Benutzer:BirgitLachner/Ortskurven mit GeoGebra untersuchen und bestimmen/Übersicht/Höhenschnittpunkt in Dreieck bei Punkt auf paralleler Geraden
Beschreibung der Ausgangssituation
Vorgehen ist eine Strecke eines Dreiecks mit den Punkten und . Der dritte Punkt des Dreiecks , die parallel zur Strecke im Abstand liegt. Für die Formparameter und gilt: .
Der Bewegungsparameter ist die 1. Koordinate des Punktes

Gesucht ist die Ortskurve für den Schnittpunkt der Höhen H in dem Dreieck, wenn sich der Punkt C auf der parallelen Geraden bewegt.

Simulationen
Mögliche Lösungswege
1.) Über die Ähnlichkeit von Dreiecken und durch die Auflösung einer Gleichung (mit Parametern)
Im Dreieck sind die zwei grünen, hier hervorgehobenen, Teildreiecke zueinander ähnlich.
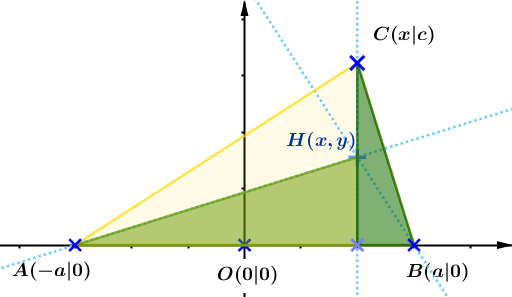
Wenn dies nicht als bekannt vorausgesetzt wird, kann über die Winkelsätze festgestellt werden, dass die Winkel in den beiden Dreiecken jeweils identisch sind. Aufgrund des Strahlensatzes kann dann eine Verhältnisgleichung (Bruchgleichung) aufgestellt werden, die nach y (siehe Zeichnung, Koordinaten von H) aufgelöst wird. Dadurch erhält man eine allgemeine Gleichung mit einem Zusammenhang von x und y.
2.) Über den Schnittpunkt von Geraden in Parameterschreibweise.
C ist ja der Schnittpunkt von zwei Geraden. Also könnte man einfach diesen Schnittpunkt bestimmen, wobei die Geradengleichungen von dem Bewegungsparameter x und den Formvariablen abhängen.
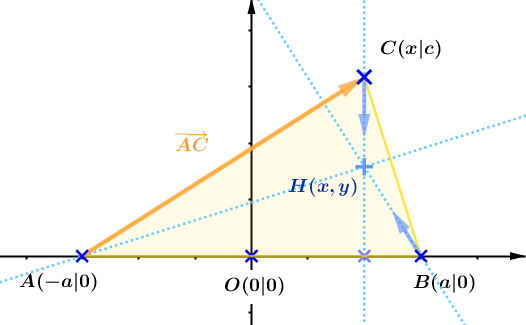
Ein einfachsten ist die Vorgehensweise, wenn man Geradengleichungen in Parameterschreibweise mit Vektoren angibt. Die Bestimmung der Ortsvektoren ergibt sich aus den Vorgaben, die Richtungsvektoren brauchen teilweise etwas Überlegungen, sind aber über die Bestimmung von senkrechten Vektoren machbar. Sinnvoll ist dabei die (im Koordinatensystem) senkrechte Höhengerade (einfacherer Richtungsvektor!) und die Höhengerade durch B zu bestimmen.
Die Nutzung einfacher Geradengleichungen nach der Art y = mx + b ist bei den Vorgaben unpraktisch, da man dann die Koordinaten von H und C anders wählen müsste.



