Potenzfunktionen - 3. Stufe: Unterschied zwischen den Versionen
K (227 Versionen importiert) |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Potenzfunktionen}} | {{Navigation verstecken|{{Lernpfad Potenzfunktionen}}|Lernschritte einblenden|Lernschritte ausblenden}} | ||
__NOTOC__ | |||
'''Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen (positiven) Stammbruch der Form <math>\textstyle \frac{1}{n}</math> mit <math>n \in \mathbb{N}^*</math> als Exponenten haben.''' | '''Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen (positiven) Stammbruch der Form <math>\textstyle \frac{1}{n}</math> mit <math>n \in \mathbb{N}^*</math> als Exponenten haben.''' | ||
| Zeile 8: | Zeile 8: | ||
=== Funktionsgraph kennenlernen === | === Funktionsgraph kennenlernen === | ||
{ | {{Box|1=Aufgabe 1|2= | ||
Rechts siehst Du den Graphen der Funktion <math>f(x)=x^{\frac 1 n}</math> für <math>n \in \{2,3,4,5,6\}</math>.<br /> | Rechts siehst Du den Graphen der Funktion <math>f(x)=x^{\frac 1 n}</math> für <math>n \in \{2,3,4,5,6\}</math>.<br /> | ||
# Beschreibe den Graphen und achte dabei auf | # Beschreibe den Graphen und achte dabei auf | ||
| Zeile 17: | Zeile 15: | ||
#* größte und kleinste Funktionswerte | #* größte und kleinste Funktionswerte | ||
# Gibt es Punkte, die allen Graphen dieser Bauart gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre> | # Gibt es Punkte, die allen Graphen dieser Bauart gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre> | ||
<ggb_applet height="450" width="900" showMenuBar="false" showResetIcon="true" id="vmtmy9jg" /> | |||
{{Lösung versteckt| | |||
: zu 1) Der Definitionsbereich ist IR<sup>+</sup><sub>0</sub>. Der kleinste Funktionswert y<math>=</math>0 wird für x<math>=</math>0 angenommen; von da aus steigen die blauen Graphen streng monoton über alle Grenzen an. | : zu 1) Der Definitionsbereich ist IR<sup>+</sup><sub>0</sub>. Der kleinste Funktionswert y<math>=</math>0 wird für x<math>=</math>0 angenommen; von da aus steigen die blauen Graphen streng monoton über alle Grenzen an. | ||
: zu 2) Man findet die Punkte (0;0) und (1;1) unabhängig von n in allen Graphen. '''Begründung:''' Es gilt 0<sup>r</sup> <math>=</math>0 und 1<sup>r</sup> <math>=</math>1 für alle <math>r \in \mathbb{R}\backslash\{0 \}</math>. | : zu 2) Man findet die Punkte (0;0) und (1;1) unabhängig von n in allen Graphen. '''Begründung:''' Es gilt 0<sup>r</sup> <math>=</math>0 und 1<sup>r</sup> <math>=</math>1 für alle <math>r \in \mathbb{R}\backslash\{0 \}</math>. | ||
}} | }} | ||
|3=Arbeitsmethode}} | |||
| | |||
=== Vergleich mit Funktionen aus Stufe 2 === | === Vergleich mit Funktionen aus Stufe 2 === | ||
{ | {{Box|1=Aufgabe 2|2= | ||
Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 1 und 2 dieses Kurses kennst (rot strichliert); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern. | Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 1 und 2 dieses Kurses kennst (rot strichliert); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern. | ||
# Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf | # Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf | ||
| Zeile 38: | Zeile 34: | ||
#* größte und kleinste Funktionswerte | #* größte und kleinste Funktionswerte | ||
# Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre> | # Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre> | ||
<ggb_applet height="450" width="900" showMenuBar="false" showResetIcon="true" id="weqjncvn" /> | |||
{{Lösung versteckt| | |||
: zu 1) Der Definitionsbereich der blauen Graphen ist nicht-negativ. Der kleinste Funktionswert y<math>=</math>0 wird für x<math>=</math>0 angenommen; von da aus steigen die blauen Graphen steng monoton an. | : zu 1) Der Definitionsbereich der blauen Graphen ist nicht-negativ. Der kleinste Funktionswert y<math>=</math>0 wird für x<math>=</math>0 angenommen; von da aus steigen die blauen Graphen steng monoton an. | ||
: zu 2) Man findet die Punkte (0;0) und (1;1) in allen blauen Graphen. Begründung: Es gilt stets 1<sup>r</sup> <math>=</math>1 für alle <math>r \in \mathbb{R}\setminus\{0\}</math>. | : zu 2) Man findet die Punkte (0;0) und (1;1) in allen blauen Graphen. Begründung: Es gilt stets 1<sup>r</sup> <math>=</math>1 für alle <math>r \in \mathbb{R}\setminus\{0\}</math>. | ||
}} | }} | ||
|3=Arbeitsmethode}} | |||
== Bezeichungen: Potenzen und Wurzeln == | == Bezeichungen: Potenzen und Wurzeln == | ||
Wir betrachten hier Potenzfunktionen mit <math>f(x)=x^{\frac 1 n}</math> , <math>n \in \mathbb{N}^*.</math> | Wir betrachten hier Potenzfunktionen mit <math>f(x)=x^{\frac 1 n}</math> , <math>n \in \mathbb{N}^*.</math> | ||
{{ | |||
{{Box|1=Merke|2= Wegen <math>x^{\frac{1}{n}}:=\sqrt[n]{x}</math> nennt man diese Funktionen auch ''Wurzelfunktionen''. Ihr Definitionsbereich ist (wie die Aufgaben 1 und 2 gezeigt haben) IR<sup>+</sup><sub>0</sub>. Beschränkt man sich auf diesen Definitonsbereich, dann ist die n-te Wurzelfunktion f mit <math>f(x)=x^{\frac 1 n}</math> die Umkehrfunktion zur Potenzfunktion g der Bauart g(x)<math>=</math> x<sup>n</sup> und g die Umkehrfunktion zu f (Näheres zur ''Umkehrfunktion'' siehe [[Potenzfunktionen_4._Stufe#Potenzfunktionen_und_ihre_Umkehrfunktionen | nächstes Kapitel]]). | |||
Im Falle n<math>=</math>2 nennt man die Wurzel "''Quadratwurzel''" und man schreibt: | Im Falle n<math>=</math>2 nennt man die Wurzel "''Quadratwurzel''" und man schreibt: | ||
| Zeile 58: | Zeile 53: | ||
Im Falle n<math>=</math>3 nennt man die Wurzel "''Kubikwurzel''", i. Z.: <font style="vertical-align:27%;"><math>x^{\frac{1}{3}}</math></font> bzw. <math>\sqrt[3]{x}</math>. | Im Falle n<math>=</math>3 nennt man die Wurzel "''Kubikwurzel''", i. Z.: <font style="vertical-align:27%;"><math>x^{\frac{1}{3}}</math></font> bzw. <math>\sqrt[3]{x}</math>. | ||
}} | |3=Merksatz}} | ||
Den Grund für diese Bezeichnungen zeigen die folgenden Beispiele: | Den Grund für diese Bezeichnungen zeigen die folgenden Beispiele: | ||
| Zeile 65: | Zeile 60: | ||
=== Beispiel: Quadratwurzeln === | === Beispiel: Quadratwurzeln === | ||
[[Datei:Diagonale_Potenzfunktionen.jpg|right|165px]] | |||
| | |||
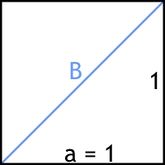
Beispielsweise ergibt sich die Länge der '''Diagonalen B in einem Quadrat''' der Seitenlänge a<math>=</math>1 über den Satz des Pythagoras <math>\left( a^2 \!\,+ a^2 = B^2 \right)</math> zu: | Beispielsweise ergibt sich die Länge der '''Diagonalen B in einem Quadrat''' der Seitenlänge a<math>=</math>1 über den Satz des Pythagoras <math>\left( a^2 \!\,+ a^2 = B^2 \right)</math> zu: | ||
:<math>a^2 + a^2 = 2 \cdot a^2 = 2 \cdot 1^2 = 2 =B^2 \quad \Rightarrow</math> <math>\quad B = \pm \sqrt{2} = \pm 2^{\frac 1 2}.</math> | :<math>a^2 + a^2 = 2 \cdot a^2 = 2 \cdot 1^2 = 2 =B^2 \quad \Rightarrow</math> <math>\quad B = \pm \sqrt{2} = \pm 2^{\frac 1 2}.</math> | ||
Die Lösung <font style="vertical-align:15%;"><math>\textstyle d=-\sqrt{2}</math></font> ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten. | Die Lösung <font style="vertical-align:15%;"><math>\textstyle d=-\sqrt{2}</math></font> ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten. | ||
[[Bild:diagonale3.jpg|right|170px]] | |||
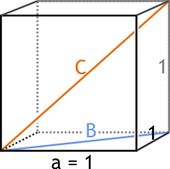
Auch die Länge der '''Raumdiagonale C im Einheitswürfel''' (das ist ein Würfel mit der Kantenlänge a=1) ergibt sich über eine analoge Rechnung aus dem Satz des Satz des Pythagoras (hier: <math>B^2 + \!\,a^2 = C^2</math>) zu: | |||
:<math>\sqrt{2}^2 + 1^2 = 2 + 1 = 3 = C^2 \quad \Rightarrow</math> <math> \quad C = \pm \sqrt{3} = \pm 3^{\frac 1 2}.</math> | :<math>\sqrt{2}^2 + 1^2 = 2 + 1 = 3 = C^2 \quad \Rightarrow</math> <math> \quad C = \pm \sqrt{3} = \pm 3^{\frac 1 2}.</math> | ||
Die Lösung ist also <font style="vertical-align:15%;"><math>\textstyle C = \sqrt{3}</math></font> angeben. | Die Lösung ist also <font style="vertical-align:15%;"><math>\textstyle C = \sqrt{3}</math></font> angeben. | ||
=== Beispiel: Kubikwurzel === | === Beispiel: Kubikwurzel === | ||
| Zeile 90: | Zeile 82: | ||
== Einfluss von Parametern == | == Einfluss von Parametern == | ||
{{ | {{Box|1=Aufgabe 3|2= | ||
Im Applet kannst Du die Parameter a und c mit den Schiebereglern verändern.<br /> | |||
# Wie beeinflusst der Parameter a die Lage des Graphen? | # Wie beeinflusst der Parameter a die Lage des Graphen? | ||
# Wie beeinflusst der Parameter c die Lage des Graphen? | # Wie beeinflusst der Parameter c die Lage des Graphen? | ||
<ggb_applet height="450" width="800" showMenuBar="false" showResetIcon="true" id="fwtzatzv" /> | |||
{{Lösung versteckt| | |||
: zu 1.) Der Parameter a bewirkt für a>1 eine Streckung des Graphen in y-Richtung, für 0<a<1 eine Stauchung in y-Richtung; für a<math>=</math>0 erhält man eine konstante Funktion mit f(x)<math>=</math>c. Wird a negativ, so wird f zu einer monoton fallenden Funktion.<br />zu 2.) Der Parameter c bewirkt eine Verschiebung des kompletten Graphen in y-Richung, da zu jedem Funktionswert y der Wert c addiert wird. | : zu 1.) Der Parameter a bewirkt für a>1 eine Streckung des Graphen in y-Richtung, für 0<a<1 eine Stauchung in y-Richtung; für a<math>=</math>0 erhält man eine konstante Funktion mit f(x)<math>=</math>c. Wird a negativ, so wird f zu einer monoton fallenden Funktion.<br />zu 2.) Der Parameter c bewirkt eine Verschiebung des kompletten Graphen in y-Richung, da zu jedem Funktionswert y der Wert c addiert wird. | ||
}}<br> | }}<br> | ||
}} | |3=Arbeitsmethode}} | ||
== *Zum Weiterdenken: Definitionsbereich der Wurzelfunktionen == | == *Zum Weiterdenken: Definitionsbereich der Wurzelfunktionen == | ||
<small>(*Zusatzinformation, freilwillige Ergänzung)</small> | <small>(*Zusatzinformation, freilwillige Ergänzung)</small> | ||
==== Einschränkung auf IR<sup>+</sup><sub>0</sub> ==== | ==== Einschränkung auf IR<sup>+</sup><sub>0</sub> ==== | ||
| Zeile 123: | Zeile 116: | ||
---- | ---- | ||
|} | '''Als nächstes erfährst du etwas über Potenzfunktionen, die auch negative Stammbrüchen im Exponenten haben.'''<br /> | ||
{{Weiter|Potenzfunktionen_-_4._Stufe|Weiter}} | |||
Version vom 25. Oktober 2018, 13:42 Uhr
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen (positiven) Stammbruch der Form mit als Exponenten haben.
Die Graphen der Funktionen f(x) = x1/n, n ∈ IN*
Funktionsgraph kennenlernen
Rechts siehst Du den Graphen der Funktion für .
- Beschreibe den Graphen und achte dabei auf
- Definitionsbereich
- Monotonie
- größte und kleinste Funktionswerte
- Gibt es Punkte, die allen Graphen dieser Bauart gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen

- zu 1) Der Definitionsbereich ist IR+0. Der kleinste Funktionswert y0 wird für x0 angenommen; von da aus steigen die blauen Graphen streng monoton über alle Grenzen an.
- zu 2) Man findet die Punkte (0;0) und (1;1) unabhängig von n in allen Graphen. Begründung: Es gilt 0r 0 und 1r 1 für alle .
Vergleich mit Funktionen aus Stufe 2
Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 1 und 2 dieses Kurses kennst (rot strichliert); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.
- Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
- Definitionsbereich
- Symmetrie
- Monotonie
- größte und kleinste Funktionswerte
- Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen

- zu 1) Der Definitionsbereich der blauen Graphen ist nicht-negativ. Der kleinste Funktionswert y0 wird für x0 angenommen; von da aus steigen die blauen Graphen steng monoton an.
- zu 2) Man findet die Punkte (0;0) und (1;1) in allen blauen Graphen. Begründung: Es gilt stets 1r 1 für alle .
Bezeichungen: Potenzen und Wurzeln
Wir betrachten hier Potenzfunktionen mit ,
Wegen nennt man diese Funktionen auch Wurzelfunktionen. Ihr Definitionsbereich ist (wie die Aufgaben 1 und 2 gezeigt haben) IR+0. Beschränkt man sich auf diesen Definitonsbereich, dann ist die n-te Wurzelfunktion f mit die Umkehrfunktion zur Potenzfunktion g der Bauart g(x) xn und g die Umkehrfunktion zu f (Näheres zur Umkehrfunktion siehe nächstes Kapitel).
Im Falle n2 nennt man die Wurzel "Quadratwurzel" und man schreibt:
Den Grund für diese Bezeichnungen zeigen die folgenden Beispiele:
Beispiel: Quadratwurzeln
Beispielsweise ergibt sich die Länge der Diagonalen B in einem Quadrat der Seitenlänge a1 über den Satz des Pythagoras zu:
Die Lösung ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten.
Auch die Länge der Raumdiagonale C im Einheitswürfel (das ist ein Würfel mit der Kantenlänge a=1) ergibt sich über eine analoge Rechnung aus dem Satz des Satz des Pythagoras (hier: ) zu:
Die Lösung ist also angeben.
Beispiel: Kubikwurzel
Das Volumen V eines Würfels (lat.: "cubus") der Kantenlänge s5 ergibt sich über:
Umgekehrt erhält man die Kantenlänge eines Würfels mit Volumen V27 durch ziehen der 3.-Wurzel:
Einfluss von Parametern
Im Applet kannst Du die Parameter a und c mit den Schiebereglern verändern.
- Wie beeinflusst der Parameter a die Lage des Graphen?
- Wie beeinflusst der Parameter c die Lage des Graphen?

- zu 1.) Der Parameter a bewirkt für a>1 eine Streckung des Graphen in y-Richtung, für 0<a<1 eine Stauchung in y-Richtung; für a0 erhält man eine konstante Funktion mit f(x)c. Wird a negativ, so wird f zu einer monoton fallenden Funktion.
zu 2.) Der Parameter c bewirkt eine Verschiebung des kompletten Graphen in y-Richung, da zu jedem Funktionswert y der Wert c addiert wird.
*Zum Weiterdenken: Definitionsbereich der Wurzelfunktionen
(*Zusatzinformation, freilwillige Ergänzung)
Einschränkung auf IR+0
Gelegentlich findet man in Büchern oder auch im Internet folgende Darstellung:
Wegen
- (-2)3 -8
erscheint das richtig zu sein, allerdings kann diese Festlegung zu Widersprüchen führen, wie das folgende Beispiel zeigt:
Um solche Fälle von Nicht-Eindeutigkeiten, aber auch um Fallunterscheidungen bei für gerade und ungerade n zu vermeiden, schränkt man den Definitionsbereich ID der Wurzelfunktionen grundsätzlich auf die nicht-negativen reellen Zahlen ein, also:
- mit und
Als nächstes erfährst du etwas über Potenzfunktionen, die auch negative Stammbrüchen im Exponenten haben.