Zylinder Pyramide Kegel/Rund um den Zylinder: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
(l korr) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 51: | Zeile 51: | ||
a) Notiere, aus welchen Flächen sich die'''Oberfläche''' eines Zylinders zusammensetzt. | a) Notiere, aus welchen Flächen sich die'''Oberfläche''' eines Zylinders zusammensetzt. | ||
b) Zeichne das Körpernetz [[ | b) Zeichne das Körpernetz [[Zylinder Pyramide Kegel/Rund um den Zylinder/Was war das nochmal?|(Was war das nochmal?)]] eines Zylinders mit Radius <math>r_{z}=1cm</math> und Höhe <math>h_{z}=3cm</math>. Beschriftung nicht vergessen! | ||
{{Lösung versteckt|1=Die Länge des Rechtecks ist gleich dem Umfang des Grundflächenkreises, also <u>nicht beliebig lang</u> zeichnen! | {{Lösung versteckt|1=Die Länge des Rechtecks ist gleich dem Umfang des Grundflächenkreises, also <u>nicht beliebig lang</u> zeichnen! | ||
|2=Hinweis einblenden|3=Hinweis ausblenden}} | |2=Hinweis einblenden|3=Hinweis ausblenden}} | ||
| Zeile 211: | Zeile 211: | ||
{{Fortsetzung|weiter=Der Satz von Cavalieri|weiterlink=../Der_Satz_von_Cavalieri}} | {{Fortsetzung|weiter=Der Satz von Cavalieri|weiterlink=../Der_Satz_von_Cavalieri}} | ||
[[Kategorie:Interaktive Übung]] | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie:R-Quiz]] | [[Kategorie:R-Quiz]] | ||
Aktuelle Version vom 17. Mai 2022, 16:58 Uhr
Hinweise
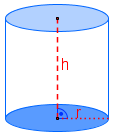
Es gibt gerade (senkrechte) und schiefe Zylinder:
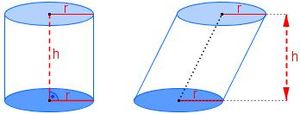
Wir betrachten hier zunächst nur gerade Zylinder. Du wirst allerdings im Laufe der Unterrichtsreihe sehen, dass Mantel- und Oberflächeninhalt, sowie das Volumen eines schiefen Zylinders genauso berechnet werden, wie bei einem geraden Zylinder. (siehe "Satz von Cavalieri")
Wo gibt es überall Zylinder?
Mantelfläche und Mantelflächeninhalt des Zylinders
Klopapierrollen und Küchenrollen sind offene Zylinder (ohne Grund- und Deckfläche), d.h. sie bestehen nur aus dem Manteleines Zylinders.
Stelle eine Formel für den Mantelflächeninhalt eines Zylinders auf. Gehe dazu schrittweise vor:
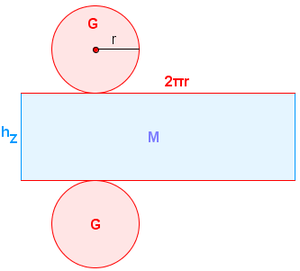
a) Stelle dir zunächst vor, du schneidest die Mantelfläche des Zylinders (von oben nach unten) auf und biegst diese zu einer ebenen Fläche. Welche ebene Figur erhältst du dadurch? Überprüfe deine Überlegung mit Hilfe der Klopapierrolle.
b) Der Mantelflächeninhalt ist gleich dem Flächeninhalt der Figur aus a). Stelle nun die Formel zur Berechnung des Mantelflächeninhalts eines Zylinders auf!
Zur Lösung musst du den Buchstabensalat unten sortieren!
Die Mantelfläche des Zylinders ist ein Rechteck. Die Breite des Rechtecks entspricht der Höhe des Zylinders. Die Länge des Rechtecks entspricht dem Umfang der Zylindergrundfläche (Kreisumfang). Der Mantelflächeninhalt ist also das Produkt aus Umfang und Höhe des Zylinders. Nun musst du dies nur noch in die Formelschreibweise übersetzen und die entsprechende Formel für den Zylinderumfang einsetzen.
Oberfläche und Oberflächeninhalt des Zylinders
a) Notiere, aus welchen Flächen sich dieOberfläche eines Zylinders zusammensetzt.
b) Zeichne das Körpernetz (Was war das nochmal?) eines Zylinders mit Radius und Höhe . Beschriftung nicht vergessen!
Stelle eine Formel für den Oberflächeninhalt des Zylinders auf. Das Körpernetz des Zylinders hilft dir dabei!
Der Oberflächeninhalt berechnet sich durch: 2+. Die Grundfläche ist ein Kreis, die Mantelfläche ein Rechteck. Die Formel für die Flächeninhalte der einzelnen Teile der Oberfläche kennst du bereits und kannst sie einsetzen.
Das Volumen des Zylinders
Überlege, wie man die Volumenformel des Zylinders von der Volumenformel eines bereits bekannten Körpers ableiten könnte. Stelle die Formel für das Zylindervolumen auf.
Bei einem Zylinder sind, ebenso wie bei einem Prisma, Grund- und Deckfläche parallel und kongruent (deckungsgleich) zueinander. Das Volumen eines Prismas berechnet sich durch . Die Grundfläche eines Prismas kann auch ein beliebiges n-Eck sein.
"Lösung: Volumenformel des Zylinders"
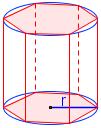
Ein Zylinder hat als Grundfläche einen Kreis, der durch n-Ecke beliebig genau angenähert werden kann. Daher kann man auch den Zylinder durch ein n-seitiges Prisma annähern (s. Abbildung).
Somit gilt auch für das Zylindervolumen .
Zusammenfassung
Bemerkung zur Schreibweise:
Bei Aufgaben, bei denen es nur um Berechnungen am Zylinder geht, benötigt man den Index "Zylinder" oder "Z" (s. Formeln unten) nicht. Allerdings ist ein solcher Index sehr hilfreich bei Aufgaben, bei denen z.B. ein Zylinder und ein Quader berechnet werden sollen. Um die einzelnen Größen (z.B. Höhe h) unterscheiden zu können, fügt man einfach einen entsprechenden Index hinzu (z.B. oder und oder ). So behält man den Überblick darüber, was nun berechnet oder eingesetzt werden soll.
Ein Zylinder mit dem Radius , der Grundfläche und der Höhe hat das Volumen :
Der Mantelflächeninhalt des Zylinders berechnet sich durch:
Für den Oberflächeninhalt des Zylinders gilt:
Übungsaufgaben
Eine Litfaßsäule ist 2,5m hoch und hat eine Werbefläche von 7,5m². Wie groß ist ihr Grundflächeninhalt?
Eine Litfaßsäule hat die Form eines Zylinders. Die Werbefläche der Säule entspricht der Mantelfläche des Zylinders.
geg.: M=7,5m²; h=2,5m
ges.: G
Lösung:
Achtung! Nicht mit dem gerundeten Wert für den Radius weiterrechnen, sondern den genauen Wert verwenden!
Bei einem Zylinder mit Radius r, Höhe h, Grundfläche G, Volumen V, Mantelflächeninhalt M und Oberflächeninhalt O sind zwei der sechs Größen gegeben. Berechne die fehlenden vier Größen und runde auf zwei Nachkommastellen.
Wichtiger Hinweis: Rechne mit den genauen Werten weiter. Verwende dazu zunächst nur die Formelschreibweise, stelle die Formelgleichung entsprechend um und vereinfache (wenn möglich). Setze erst danach die entsprechenden Zahlen ein und berechne.
(Das Umformen von Gleichungen mit Variablen soll dadurch trainiert werden. Bei manchen Aufgaben werden beispielsweise gar keine Längen oder Größen wie Volumen und Radius angegegeben und du musst die entsprechende Formel anhand der Variablen aufstellen und zusammenfassen.)
r h G V M O a) 5,2 cm ? ? ? ? ? ? ? ? 0,098 dm³ ? ? ? ? b) 64 dm³ 0,72 m²
Einheiten: a) in cm (bzw. cm², cm³); b) in dm (bzw. dm², dm³)
Hausaufgabe für die nächste Stunde
Bearbeite in deinem Schulbuch (Lambacher Schweizer, Ausgabe 2010) auf Seite 20 folgende Aufgaben:
- Nr.5: Gib das Ergebnis in Zentimeter an!
- Nr.6: Die Volumen- und Oberflächenberechnung einer der abgebildeten Körper haben wir bereits im Unterricht besprochen. Berechne nun zwei der restlichen Körper.
Setze auch hier wieder die Zahlen erst ganz am Ende ein, nachdem du die Formel entsprechend umgeformt und weitgehend vereinfacht hast (s. vorherige Aufgabe)!
(Du findest unten für alle Körper aus Nr.6 die Lösungen! Du kannst die restlichen Aufgaben somit als Übung für die Klassenarbeit oder die anstehende HÜ nutzen!)
Lösung zu S.20 Nr.5:geg.:
(benötigt man hier gar nicht!)
ges.:
Lösung:
Antwort: Das Wasser steht ca. 39,3cm hoch.
Abschlusstest: Multiple-Choice-Quiz
1. Der Durchmesser eines Kreises ist… (!der Radius) (der doppelte Radius) (!die Verbindung zweier Kreispunkte) (! der halbe Radius)
2. Die Oberfläche eines Zylinders besteht aus… (!zwei beliebigen Kreisen) (!Dreieck) (Rechteck) (!Raute) (zwei kongruenten Kreisen)
3. Was stellt der Kreis bei einem Zylinder dar? (Deckfläche) (!Mantelfläche) (!Oberfläche) (Grundfläche) (!Grundflächeninhalt)
4. Die Formel für das Volumen eines Zylinders lautet: () (!) () ()