Zylinder Pyramide Kegel/Rund um die Pyramide

Zylinder Pyramide Kegel

1. Einführungstests zu bekannten Inhalten
2. Rund um den Zylinder
3. Der Satz von Cavalieri
4. Rund um die Pyramide
5. Rund um den Kegel
6. Zusatzaufgaben

< zurück zu Mathematik-digital.de

Bauwerke des Menschen

• 

  Die Pyramiden von Gizeh

• 

  Glaspyramide im Innenhof des Louvre in Paris

• 

  Die Pyramide auf dem Marktplatz von Karlsruhe

Eigenschaften einer Pyramide

Augabe 1

Fülle den Lückentext aus!

Verbindet man die Ecken eines ebenen n-Ecks mit einem Punkt S außerhalb der Ebene des n-Ecks, so erhält man eine n-seitige Pyramide. Das n-Eck heißt Grundfläche und S nennt man Spitze der Pyramide. Der Abstand der Spitze S zur Grundfläche G ist die Höhe h der Pyramide. Der Schnittpunkt der Höhe mit der Grundfläche (bzw. der Ebene in der die Grundfläche liegt) heißt Höhenfußpunkt $H_{F}$. Die Seiten zwischen Pyramidenspitze S und Ecken der Grundfläche nennt man Seitenkanten. Die Seiten der Grundfläche werden auch Grundkanten genannt. Die Seitenflächen einer Pyramide sind immer Dreiecke und bilden zusammen die Mantelfläche.

Pyramiden können also jedes beliebige n-Eck als Grundfläche haben. Die Anzahl der Seitenflächen ist gleich der Anzahl der Ecken!
Hier siehst du drei Beispiele von Pyramiden mit verschiedenen Grundflächen:

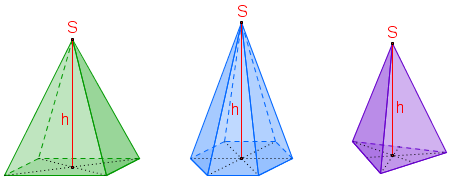
Pyramiden können sich aber nicht nur in ihrer Grundfläche und somit in der Anzahl der Seitenflächen unterscheiden. Man differenziert auch zwischen geraden (bzw. senkrechten) und schiefen Pyramiden.
Betrachte dazu auch das GeoGebra Applet "Gerade und schiefe Pyramide".

Aufgabe 2

Gerade und schiefe Pyramiden
Fülle die Lücken aus! Das Lösungswort steht jeweils verdreht hinter der Lücke.

Eine gerade Pyramide zeichnet sich dadurch aus, dass die Höhe innerhalb der Pyramide liegt und der Höhenfußpunkt $H_{F}$ mit dem Schnittpunkt der Diagonalen der Grundfläche zusammenfällt (regelmäßige Pyramide!). Die Spitze S liegt also senkrecht über dem "Mittelpunkt" der Grundfläche.
Bei einer schiefen Pyramide liegt die Spitze S nicht senkrecht über dem Diagonalenschnittpunkt der Grundfläche. Die Höhe kann sogar außerhalb der Pyramide liegen, so dass der Höhenfußpunkt $H_{F}$ nicht mehr in der Grundfläche liegt.

Hinweis: Innerhalb der Lerneinheit werden ausschließlich gerade Pyramiden mit regelmäßiger 3-, 4- oder 6-seitiger Grundfläche berechnet!

Volumen der Pyramide

Experimentelle Bestimmung der Volumenformel der Pyramide>

Aufgabe 3

Vorne am Pult liegen gebastelte (offene) quadratische Pyramiden und Quader. Gleichfarbige Pyramiden und Quader bilden jeweils ein "Paar". Die beiden Körper haben die gleiche Höhe und gleich große Grundflächen.
Bei den Quadern findest du eine Markierung, welche die eigentliche Höhe des Quaders bzw. die Begrenzung des Körpers anzeigt. Der Überstand ist nur zur besseren Handhabung beim Experimentieren gedacht und gehört nicht mehr zu dem Körper!

Durchführung des Experiments:

• Nimm dir ein "Körperpaar", eine Portion Reis, einen Trichter und eine Schüssel zum Unterstellen.
  
• Fülle die Pyramide randvoll mit Reis (Überstand abstreichen) und schütte ihn in den Quader um.
  
• Wiederhole den Vorgang so oft, bis der Quader bis zur Markierung mit Reis gefüllt ist.

Was stellst du fest?
Welcher Zusammenhang besteht zwischen den Volumina von Quader und Pyramide, wenn diese den gleichen Grundflächeninhalt und die gleiche Höhe besitzen?

Die Ergebnisse mit gebastelte Körpern sind natürlich nie 100% genau. Wenn du aber ordentlich arbeitest, solltest du ein recht gutes Ergebnis bekommen!

Du hast nun auf der Grundlage experimenteller Ergebnisse eine Formel für das Volumen einer Pyramide aufgestellt. Im Experiment hast du allerdings das Ergebnis nur für die verwendete Pyramide überprüfen können.

Im Folgenden muss nun gezeigt werden, dass die von dir gefundene Volumenformel tatsächlich gilt und zwar nicht nur für eine bestimmte Pyramide, sondern für alle Arten von Pyramiden! Dazu geht man schrittweise vor:

Zunächst leitet man die Volumenformel für eine spezielle Pyramide her und zeigt anschließend, dass dies auch für andere Pyramiden gilt.

Herleitung der Volumenformel für eine spezielle Pyramide

Ein Würfel mit der Kantenlänge a kann durch seine Raumdiagonalen in sechs kongruente Pyramiden mit quadratischer Grundfläche zerlegt werden. Dies siehst du in der Abbildung und auch im folgenden GeoGebra-Applet (hier kannst du dir Hilfsobjekte anzeigen lassen).

Aufgabe 4

Du sollst nun eine Formel für das Volumen einer der oben abgebildeten Pyramiden (mit quadratischer Grundfläche) herleiten. Betrachte dazu beispielsweise die rote Pyramide 1 und blende ihre Höhe ein. Ziel ist ein Term für das Volumen abhängig von der Grundfläche und der Höhe der Pyramide.

Fordere dich selbst einmal heraus und versuche zumindest einen Ansatz für die Herleitung der Volumenformel selbst aufzustellen! Falls du gar nicht weiterkommst oder du keine Idee hast, dann klicke unten auf "Lösung anzeigen" und leite die Formel mit Hilfe des Lückentextes her.

Notiere die wichtigsten Schritte der Herleitung an entsprechender Stelle auf deinem Laufzettel!

Es wird deutlich, dass alle sechs Pyramiden die gleiche quadratische Grundfläche, die gleiche Höhe und die gleiche Spitze besitzen.
Die Spitze der Pyramiden ist genau die Mitte des Würfel-Inneren.
Für das Volumen des Würfels mit Kantenlänge a gilt: $V_{w}=$ $a^{3}$
Da der Würfel in sechs kongruente Pyramiden aufgeteilt wurde, folgt für das Volumen der Pyramide 1:
$V_{p}=$ $\frac{1} {6}\cdot a^{3}$

Außerdem ist die Grundfläche der Pyramide $G=$ $a^{2}$ und die Höhe $h=$ $\frac{1} {2}$ $\cdot$ $a$.
Damit lässt sich das Pyramidenvolumen auch als ein Vielfaches des Produktes von Grundfläche und Höhe schreiben:
$V_{p}=\frac{1} {6}a^{3}=$ $\frac{1} {3}a^{2}$ $\cdot$ $\frac{1} {2} a$ = $\frac{1} {3}G\cdot h$

Weiteres Beispiel

Man kann einen Würfel auch in drei kongruente, schiefe Pyramiden zerlegen (s. Fotos). Dauraus folgt für das Volumen einer der Pyramiden ebenfalls $V=\frac{1} {3} G\cdot h$.
Die Spitzen der Pyramiden zeigen alle in die gleiche Ecke des Würfels.

Du kannst dir das Modell, welches auch auf den Fotos abgebildet ist, vorne am Pult anschauen oder drei der selbst gebastelten Pyramiden verwenden.

Von der speziellen zur allgemeinen Pyramide

Du hast die Gültigkeit der Formel $V=\frac{1} {3} G\cdot h$ nun für eine quadratische Pyramide mit $h=\frac{1} {2}a$ gezeigt, als auch im Modell für eine quadratische Pyramide mit $h=a$ überprüfen können.
Jetzt muss gezeigt werden, dass diese Formel auch für das Volumen einer beliebigen n-seitigen Pyramide gilt. Dazu muss folgender Satz bewiesen werden:

Satz

Zwei Pyramiden mit gleichem Grundflächeninhalt und gleicher Höhe haben das gleiche Volumen.

Das klingt stark nach dem Satz von Cavalieri! Allerdings fehlt hierzu noch ein Kriterium. Nach Cavalieri sind zwei Körper volumengleich, wenn der Grundflächeninhalt und die Höhe gleich sind, als auch alle zur Grundfläche parallelen Schnittflächen in gleicher Höhe den gleichen Flächeninhalt haben. Es muss also gezeigt werden, dass Pyramiden mit gleichem Grundflächeninhalt und gleicher Höhe auf jeder Höhe (parallel zur Grundfläche) gleich große Schnittflächen besitzen!

Aufgabe 5

Im folgenden Geogebra-Applet kannst du dich in einem ersten Schritt anschaulich davon überzeugen, dass der obige Satz gilt.
Im zweiten Schritt sollst du die Gültigkeit des Satzes mit Hilfe der Veranschaulichung zeigen.
Im letzten Schritt sollst du mit Hilfe der Geogebra-Datei überprüfen, ob dies nun auch für schiefe Pyramiden (mit gleicher Höhe und gleich großer Grundfläche) gilt.

1. Ziehe am Schieberegler k, um die Höhe der Schnittfläche zu verändern. Was fällt dir auf? Formuliere in eigenen Worten.
2. Überprüfe, ob dies auch für schiefe Pyramiden gilt! Ziehe dazu an dem grünen Punkt S₂ und beobachte was passiert.

Beweis:
Versuche erst einmal selbst einen Beweis zu führen! Falls du nicht weiter kommst, nutze zuerst die Tipps und versuche es nochmal, bevor du dir die Lösung anschaust!

Es liegt hier eine Ähnlichkeitsabbildung vor! Dabei werden die Grundflächen auf die jeweiligen Schnittflächen abgebildet!

Welcher Zusammenhang besteht zwischen den Flächeninhalten der Fläche A und der Bildfläche A' bei einer solchen Ähnlichkeitsabbildung?

Voraussetzung: G₁ = G₂

S₁ und S₂ sind Streckzentren einer zentrischen Streckung von G₁ auf G₁' bzw. von G₂ auf G₂'. Der Streckfaktor ist jeweils $k=\frac{h_{s} } {h}$.
G₁ ist also ähnlich zu G₁' und G₂ ist ähnlich zu G₂'.
$\Rightarrow$ G₁' = k²G₁ und G₂' = k²G₂

Da nach Voraussetzung G₁ = G₂

$\Rightarrow$ G₁' = G₂'

Nun bist du endlich am Ziel und du kannst eine allgemeine Formel zur Berechnung des Pyramidenvolumens aufstellen, welche auch wirklich für jede beliebige Pyramide gilt!

Übungsaufgaben zur Berechnung des Pyramidenvolumens

Zur Berechnung des Pyramidenvolumens benötigt man die Maße der Pyramidengrundfläche und der Höhe. Diese sind allerdings nicht immer direkt gegeben und müssen erst aus den angegebenen Seitenlängen berechnet werden. Bei der Berechnung muss man mit sogenannten Hilfsdreiecken arbeiten. Bei den Hilfsdreiecken handelt es sich um rechtwinklige Dreiecke, wobei bereits zwei der Seiten gegeben sind. Die dritte Seite lässt sich dann einfach durch Anwendung des Satzes von Pythagoras berechnen!

Aufgabe 6

Bearbeite die Aufgaben a) und b) zur Volumenberechnung einer quadratischen Pyramide auf deinem Laufzettel.

Im folgenden Geogebra-Applet kannst du dir anschauen, welche Hilfsdreiecke man zur Berechnung verschiedener Seiten verwenden kann.
Zeichne auf deinem Laufzettel jeweils passend zur Aufgabe die benötigten Hilfsdreiecke in die quadratische Pyramide ein. Stelle immer erst die entsprechende Formel auf und setze erst anschließend die Werte ein!

 Ausführliche Lösung zu Aufgabe 6

Mantelfläche und Mantelflächeninhalt

Aufgabe 7

Fülle den Lückentext zu Mantelfläche und Mantelflächeninhalt auf deinem Laufzettel aus!

Zeige die Lösung deiner Lehrerin!

Oberfläche und Oberflächeninhalt

Körpernetz einer Pyramide

Schneidet man eine Pyramide entlang der Seitenkanten auf und klappt die Seitenflächen in die Ebene der Grundfläche, so erhält man das Netz der Pyramide.
Ebenso kann man eine Pyramide entlang von Seiten- und Grundkanten aufschneiden und in die Grundflächenebene klappen, um ein Körpernetz zu erhalten. Dabei muss man beachten, dass keine Dreicksfläche komplett abgetrennt wird! Das Netz eines Körpers ist immer eine zusammenhängende Fläche, die wieder zu dem vollständigen Körper gefaltet werden kann!
Das folgende Beispiel zeigt ein Körpernetz einer quadratischen Pyramide, welche entlang zweier Seiten- und zweier Grundkanten aufgeschnitten wurde:

Aufgabe 8

Zeichne das Körpernetz einer regelmäßigen dreiseitigen oder vierseitigen Pyramide.

Als Hilfestellung kannst du die Holzpyramiden vorne am Pult verwenden!

Zur Überprüfung eurer Ergebnisse stehen auch zwei Modelle von Körpernetzen zur Verfügung

Aufgabe 9

Stelle eine Formel zur Berechnung des Oberflächeninhalts einer 4-seitigen Pyramide auf!

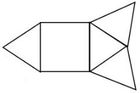
Zusammenfassung

Achtung

Hier geht es zur Zusammenfassung

Denkt an die Gestaltung eurer Formelsammlung!

Übungsaufgaben: Berechnungen rund um die Pyramide

Aufgabe 10

Die große Glaspyramide im Innenhof des Louvre in Paris hat eine quadratische Grundfläche mit einer Seitenlänge von 35m und eine Höhe von 22m. Wie groß ist der Innenraum und die Glasoberfläche?
Mache zunächst eine Skizze der Glaspyramide und eventuell benötigter Hilfsobjekte (s. Aufgabe 6).

Hinweis: Stelle (wie in den vorherigen Aufgaben) immer zuerst eine Formel auf, forme wenn nötig um und setze dann erst die Zahlenwerte ein! (Nicht mit gerundeten Werten weiterrechnen!)

 Lösung zu Aufgabe 10

Aufgabe 11

Berechnungen an einer regelmäßigen sechsseitigen Pyramide

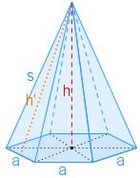Bearbeite Aufgabe 11 auf deinem Laufzettel!

zu Aufgabe 11 b)

GeoGebra Applet "Berechnungen an einer regelmäßigen sechsseitigen Pyramide"

2=zu Aufgabe 11b

 Ausführliche Lösung zu Aufgabe 11

Abschlusstest: Multiple-Choice-Quiz

Aufgabe 12

1. Wie viele Ecken hat eine dreiseitige Pyramide? (!3) (!5) (4)

2. Wie viele Kanten hat eine sechsseitige Pyramide? (!6) (!14) (!10) (12)

3. Wie viele Flächen hat eine quadratische Pyramide? (!4) (!6) (5)

4. Wie lautet die Volumenformel einer regelmäßigen dreiseitigen Pyramide mit Grundkantenlänge a? ($V=\frac{1} {3}G\cdot h$) ($V=\frac{\sqrt{3} } {12}a^{2}\cdot h$) (!$V=\frac{\sqrt{3} } {4}a^{2}\cdot h$) ($V=\frac{1} {6}a\cdot h_{a} \cdot h$)

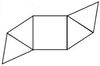
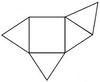
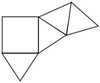
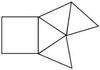
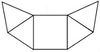
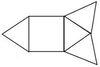
5. Falte gedanklich die verschiedenen Körpernetze zu einer quadratischen Pyramide und finde heraus, welches Netz keine Pyramide ergibt!
(!)(!)(!)(!)(!)()(!)

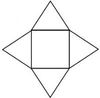Rund um den Kegel