Zylinder Pyramide Kegel/Rund um den Kegel

Zylinder Pyramide Kegel

1. Einführungstests zu bekannten Inhalten
2. Rund um den Zylinder
3. Der Satz von Cavalieri
4. Rund um die Pyramide
5. Rund um den Kegel
6. Zusatzaufgaben

< zurück zu Mathematik-digital.de

Der Kegel - Eine kleine Einführung

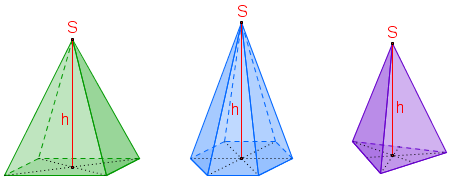
In der vorherigen Lerneinheit hast du die Pyramide mit einem beliebigen Vieleck als Grundfläche kennengelernt.
Ersetzt man nun das Vieleck der Grundfläche durch einen Kreis, so erhält man einen verwandten Spitzkörper:den Kegel!


. . . .. . . . . . . .

Ob Eistüte, Pylonen oder Turmspitzen, man findet sehr häufig kegelförmige Objekte in unserer Lebenswelt.

Eigenschaften des Kegels

Aufgabe 1

Fülle den Lückentext aus!

Ein Kegel ist ein Körper, dessen Grundfläche ein Kreis (Grundkreis) ist.
Die Mantelfläche des Kegels ist gewölbt. Der Abstand der Spitze S zur Grundfläche ist die Höhe des Kegels. Eine Verbindungsstrecke vom Kreisrand zur Kegelspitze heißt Mantellinie und wird mit "s" beschriftet.
Ebenso wie bei der Pyramide unterscheidet man auch hier zwischen geraden (senkrechten) und schiefen Kegeln. Schaue dir dazu das folgende Geogebra-Applet an.
Für uns sind allerdings nur gerade Kegel von Bedeutung.

Ziehe an der Kegelspitze S und beobachte, was passiert.

Mantelfläche und Mantelflächeninhalt

Aufgabe 2

Die Mantelfläche des Kegels

a) Stelle dir vor, du schneidest einen senkrechten Kegel entlang einer Mantellinie auf und breitest den Mantel eben aus. Beschreibe die geometrische Figur, die du für die Mantelfläche erhälst.

Beispiel:
Die Mantelfläche des Zylinders ist ein Rechteck. Die Breite des Rechtecks ist gleich der Höhe des Zylinders, die Länge des Rechtecks ist gleich dem Umfang des Zylinders.

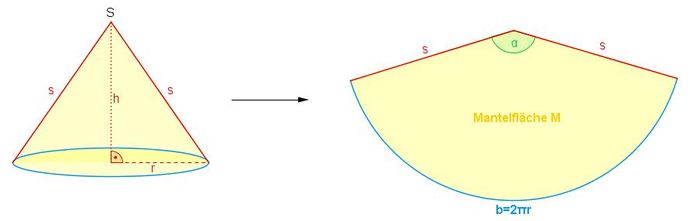
Die Mantelfläche des Kegels ist ein Kreisausschnitt (Kreissektor). Der Radius des Kreisausschnittes ist die Länge der Mantellinie s. Die Bogenlänge b ist der Umfang des Kegels.

b) Zeichne die Mantelfläche eines Kegels und beschrifte sie entsprechend.

Aufgabe 3

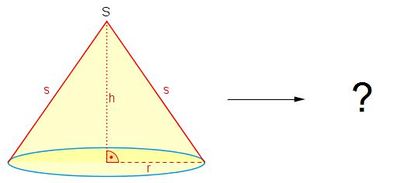
Der Mantelflächeninhalt des Kegels
Der Mantelflächeninhalt des Kegels berechnet sich über folgende Formel:
$M_{K}=\frac {1} {2} b\cdot s=\pi \cdot r\cdot s$

Versuche diese Formel herzuleiten!
Gehe dazu schrittweise vor und zeige zuerst, dass $M_{K}=\frac {1} {2} b\cdot s$ ist. Nutze auch die beschriftete Zeichnung der Mantelfläche als Hilfestellung!

Der Mantelflächeninhalt des Kegels entspricht dem Flächeninhalt des Kreisausschnittes mit Radius s und Bogenlänge b.

• b ist die Bogenlänge des Kreisaussektors mit Radius s und gleichzeitig der Umfang des Kegels mit Radius r!

Hier findest du verschiedene Tipps, wie du vorgehen kannst (wenn du nicht weiter kommst).

• Stelle zunächst eine Formel für die Bogenlänge b (bzw. den "Umfang" des Kreisausschnittes) und für den Flächeninhalt des Kreisausschnittes (also den Mantelflächeninhalt des Kegels) auf.
  
• Stelle nun einen Zusammenhang zwischen Bogenlänge und Flächeninhalt des Kreisausschnittes her!

Zusammenhang zwischen Bogenlänge und Flächeninhalt des Kreisausschnittes:

Stelle die Formel für die Bogenlänge b nach $\pi$ um und setze dies in die Formel für den Mantelflächeninhalt des Kegels ein! Nun kannst du noch kürzen und du erhälst die Formel $M_{K}=\frac {1} {2} b\cdot s$.

Die Bogenlänge b ist gleich dem Umfang des Kegels mit Radius r! Somit kannst du für b oben die Formel für den Kegelumfang einsetzen, kürzen und du erhälst die Formel

$M_{K}=\frac {1} {2} b\cdot s=\pi \cdot r\cdot s$

Aufgabe 4

Der Mittelpunktswinkel $\alpha$ des Kreissektors (bzw. der Mantelfläche)

Stelle eine Gleichung zur Berechnung des Mittelpunktwinkels $\alpha$ auf!

Dazu muss man eine Verhältnisgleichung aufstellen!

Der Winkel $\alpha$ des Kreisausschnitts verhält sich zum Winkel des vollen Kreises wie ...

... die Bogenlänge des Kreisausschnittes (=Umfang des Kegels mit Radius r) zum Umfang des vollen Kreises mit Radius s!

Anmerkung:

Über den Zusammenhang zwischen Mittelpunktswinkel $\alpha$, dem Vollkreiswinkel und den beiden zu betrachtenden Radien r und s kann man ebenfalls die Formel für den Mantelflächeninhalt aufstellen:
$M_{K}=\pi s^{2}\cdot \frac {\alpha } {360^{o}}=\pi s^{2}\cdot \frac {r} {s} =\pi \cdot r\cdot s$
Die oben aufgestellte Verhältnisgleichung wird einfach in die bereits bekannte Flächeninhaltsformel des Kreissektors eingesetzt!

Oberfläche und Oberflächeninhalt

Aufgaben 5

Notiere auf deinem Laufzettel, wie sich die Oberfläche eines Kegels zusammensetzt und stelle eine Formel für den Oberflächeninhalt auf.

Die Oberfläche eines Kegels setzt sich aus einem Kreis mit Radius r (Grundfläche) und einem Kreisausschnitt mit Radius s und Bogenlänge b zusammen.

$O_{K}=G+M=\pi r^{2}+\pi r\cdot s$

Volumen des Kegels

Aufgabe 6

Experimentelle Bestimmung des Kegelvolumens mit Hilfe der beiden abgebildeten Füllkörper:

Das Experiment wird vor der gesamten Klasse durchgeführt!

Beschreibe das Experiment auf deinem Laufzettel und notiere das Ergebnis!

Aufgabe 7

Herleitung des Kegelvolumens

Beweise, dass ein Kegel und eine Pyramide mit gleichem Grundflächeninhalt und gleicher Höhe auch gleiches Volumen besitzen!
Nutze dazu auch das folgende Geogebra-Applet, bei dem du dich im ersten Schritt anschaulich von der Richtigkeit der Aussage überzeugen kannst. Schreibe anschließend einen allgemeingültigen Beweis auf.

Der Beweis kann analog zu dem Beweis aus Aufgabe 5 der Lerneinheit "Rund um die Pyramide" geführt werden (Volumenvergleich zweier Pyramiden mit gleichem Grundflächeninhalt und gleicher Höhe)!

Stichworte: Zentrische Streckung!

Hier geht es zur Zusammenfassung!

Übungsaufgaben: Berechnungen rund um den Kegel

Aufgabe 8

Aus einem Kreisausschnitt wird ein Trichter geformt (s. Abbildung). Welches Volumen fasst der Trichter?

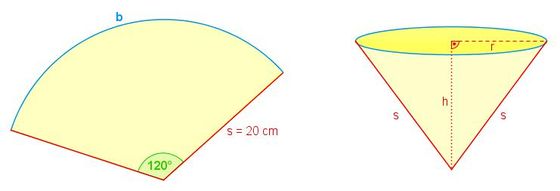
Der Trichter ist ein Kegel. Zur Berechnung des Volumens benötigen wir den Radius r und die Höhe h des Kegels.
Die Bogenlänge b des Kreisausschnitts mit Radius s berechnet sich durch:

$b=2\pi s\cdot \frac {\alpha } {360^{o} }=\pi s\cdot \frac {\alpha } {180^{o} }=\pi \cdot 20cm \cdot \frac {120^{o} } {180^{o} }=\frac {40\pi } {3} cm \approx 41,89cm$

Die Bogenlänge b entspricht dem Umfang des Grundkreises des Kegels mit Radius r, also $b=2\pi r$!

$\Rightarrow r= \frac {b} {2\pi }=\frac {40\pi } {3} \cdot \frac {1} {2\pi } cm= \frac {20} {3}cm \approx 6,67 cm$

Die Höhe h wird über den Satz von Pythagoras berechnet (oben in der Abbildung kannst du das benötigte rechtwinklige Dreieck erkennen!):
$h=\sqrt {s^{2}-r^{2} }= \sqrt {\left(20cm\right)^{2}-\left(\frac {20} {3}cm\right)^{2} } = \sqrt {\frac {3200} {9}cm^{2} } \approx 18,86 cm$
(Hier könnte man jetzt noch teilweise die Wurzel ziehen! Also $\sqrt {\frac {3200} {9}cm^{2} }=\frac {20} {3}\cdot \sqrt {8}cm$)
Nun kann das Kegelvolumen berechnet werden:
$V=\frac {1} {3}\pi r^{2}\cdot h= \frac {1} {3} \pi \cdot \left(\frac {20} {3}\right)^{2} \cdot \sqrt {\frac {3200} {9} }cm \approx 877,61 cm^{3}$

Der Trichter hat ein Volumen von ungefähr 877,61 cm³, also weniger als ein Liter!

Aufgabe 9

Bearbeite im Buch (Lambacher Schweizer, Ausgabe 2010) auf Seite 26 Nr. 6 a), b) und c)!

ODER

Bearbeite im Buch (Fokus Mathematik, Ausgabe 2016) auf Seite 49 Nr. 14!

Die Lösungen werden gemeinsam in der Klasse besprochen!

Zusatzaufgaben