Beschreibende Statistik/Klassenbildung/Klassen mit gleicher Klassenbreite: Unterschied zwischen den Versionen
main>Nina Krämer Keine Bearbeitungszusammenfassung |
main>Nina Krämer Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Für die <span style="background:yellow">Anzahl der Klassen</span> gilt die folgende Regel, <br /> | |||
wobei <math>n</math> der Stichprobenumfang ist: | |||
:: <math>k \approx \sqrt{n}</math> | |||
<br /> | |||
<!-- Fortsetzung 1 Beispiel Körpergröße (in cm) --> | |||
{|style="color: black; background-color: #FFFFE0;border-left:solid 2px #FFB90F;border-right:solid 2px #FFB90F;border-top:solid 2px #FFB90F;border-bottom:solid 2px #FFB90F;font-size:100%;font-size:100%;" | |||
|colspan="8" |<u>'''Fortsetzung Beispiel Körpergröße (in cm)'''</u> | |||
Im Beispiel ist | |||
:: <math>n=25</math>. | |||
Also gilt für die Anzahl der Klassen | |||
:: <math>k \approx \sqrt{25}=5</math>. | |||
|} | |||
<!-- Ende Fortsetzung 1 Beispiel Körpergröße (in cm) --> | |||
<br /> | |||
Eine Klasse ist ein Teil der <span style="background:yellow">Spannweite <math>R</math></span> (<math>R</math> für Range,dem englischen Begriff für Spannweite), also ein Teil der Differenz zwischen der größten Merkmalsausprägung <math>x_{max}</math> und der kleinsten Merkmalsausprägung <math>x_{min}</math>. | |||
<br /> | |||
<!-- Fortsetzung 2 Beispiel Körpergröße (in cm) --> | |||
{|style="color: black; background-color: #FFFFE0;border-left:solid 2px #FFB90F;border-right:solid 2px #FFB90F;border-top:solid 2px #FFB90F;border-bottom:solid 2px #FFB90F;font-size:100%;font-size:100%;" | |||
|colspan="8" |<u>'''Fortsetzung Beispiel Körpergröße (in cm)'''</u> | |||
Im Beispiel ist | |||
:: <math>x_{max}=200</math> und | |||
:: <math>x_{min}=151</math> , | |||
somit gilt für die Spannweite | |||
:: <math>R=x_{max}-x_{min}=200-151=49</math>. | |||
|} | |||
<!-- Ende Fortsetzung 2 Beispiel Körpergröße (in cm) --> | |||
<br /> | |||
Die <span style="background:yellow">Klassenbreite <math>b</math></span> ist der Quotient aus Spannweite und Klassenanzahl. | |||
<br /> | |||
<!-- Fortsetzung 3 Beispiel Körpergröße (in cm) --> | |||
{|style="color: black; background-color: #FFFFE0;border-left:solid 2px #FFB90F;border-right:solid 2px #FFB90F;border-top:solid 2px #FFB90F;border-bottom:solid 2px #FFB90F;font-size:100%;font-size:100%;" | |||
|colspan="8" |<u>'''Fortsetzung Beispiel Körpergröße (in cm)'''</u> | |||
Im Beispiel ist die Klassenbreite also | |||
<math>b=\frac{Spannweite} {Anzahl der Klassen}=\frac{49} {5}=9,8 \approx 10</math>. | |||
|} | |||
<!-- Ende Fortsetzung 3 Beispiel Körpergröße (in cm) --> | |||
<br /> | |||
Bei der Zuordnung der Merkmalsausprägungen ist darauf zu achten, dass sich die Klassen nicht überschneiden. Sonst könnte es passieren, dass eine Merkmalsausprägung zwei Klassen zugeordnet wird. | |||
Beachten Sie: | |||
Wählen Sie einen geeigneten Startwert als untere Klassengrenze (die in der Regel nicht zur Klasse gehören sollte) der ersten Klasse, addieren Sie die Klassenbreite um die obere Klassengrenze (diese gehört zur Klasse) zu erhalten. | |||
Die obere Klassengrenze der vorangegangenen Klasse wird die untere Grenze der nächsten Klasse. | |||
Und so fährt man fort, bis alle Klassen definiert sind. | |||
<br /> | |||
<!-- Merke Klassen,Klassenanzahl, Spannweite, Klassenbreite --> | |||
<!-- Merke --> | |||
{{Merke-M||1= | |||
Die einzelnen <span style="background:yellow">Klassen</span> bezeichnet man mit <math>k_i</math>, wobei <math>i=</math> <math>1;2;\dots;k-1;k</math> gilt. | |||
<span style="background:yellow">Klassenanzahl</span>: | |||
:: <math>k \approx \sqrt{n}</math> | |||
<span style="background:yellow">Spannweite</span>: | |||
:: <math>R= x_{max}-x_{min}</math> | |||
<span style="background:yellow">Klassenbreite</span>: | |||
:: <math>b=\frac{Spannweite}{Anzahl der Klassen}=\frac{R}{k}</math> | |||
}} | |||
<!-- Ende Merke Klassenanzahl, Spannweite, Klassenbreite --> | |||
<br /> | |||
<!-- Fortsetzung 4 Beispiel Körpergröße (in cm) --> | |||
{|style="color: black; background-color: #FFFFE0;border-left:solid 2px #FFB90F;border-right:solid 2px #FFB90F;border-top:solid 2px #FFB90F;border-bottom:solid 2px #FFB90F;font-size:100%;font-size:100%;" | |||
|colspan="8" |<u>'''Fortsetzung Beispiel Körpergröße (in cm)'''</u> | |||
Man bestimmt nun die fünf Klassen der Breite 10 und beachtet dabei, dass die Klassen sich nicht überschneiden dürfen. | |||
Dann bestimmt man die absoluten Häufigkeiten der einzelnen Klassen, dabei werden alle Merkmalsausprägungen gezählt, die zu der jeweiligen Klasse gehören. | |||
Dann berechnet man die relativen Häufigkeiten der einzelnen Klassen. | |||
<!-- Tabelle Klassierte Körpergröße HHU5 --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
|- | |||
! colspan="7" | Klassierte Körpergrößen HHU5 2012/2013 | |||
|- | |||
| <math>k_i</math> | |||
|| <math>150 < a_i \le 160</math> || <math>160 < a_i \le 170</math> || <math>170 < a_i \le 180</math> || <math>180 < a_i \le 190</math> || <math>190 < a_i \le 200</math> || Summe | |||
|- | |||
| <math>H(k_i)</math> || 3 || 6 || 5 || 4 || 7 || 25 | |||
|- | |||
| <math>h(k_i)</math> || 12 % || 24 % || 20 % || 16 % || 28 % || 100 % | |||
|} | |||
</div> | |||
<!-- Ende Klassierte Tabelle Körpergröße HHU5 --> | |||
|- | |||
| colspan="7"| | |||
Diese Darstellung ist zunächst eher objektiv und der Leser der Tabelle wird nicht in die Irre geleitet. Festzuhalten ist, das es sich um eine Klasse mit eher großen Schülern handelt. | |||
|} | |||
<!-- Ende Fortsetzung 4 Beispiel Körpergröße (in cm) --> | |||
<!-- Einführungsbeispiel - Teil 6 --> | |||
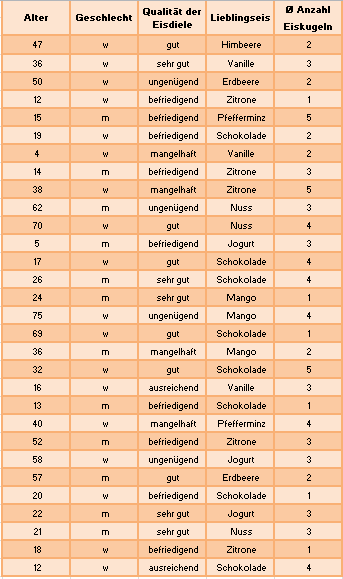
[[Datei:Umfrage Eisdiele Urliste.PNG|rechts|Einführung Merkmale und Merkmalsausprägungen]] | |||
{|style="color: black; background-color: #FFFAFA;border-left:solid 2px #CD0000;border-right:solid 2px #CD0000;border-top:solid 2px #CD0000;border-bottom:solid 2px #CD0000;font-size:100%;font-size:100%;" | |||
|colspan="4" | | |||
<u>'''Einführungsbeispiel - Teil 6.1'''<br /></u> | |||
Bei der Umfrage der Eisdiele "Rabe" weist das Merkmal "Alter" sehr viele verschiedene Merkmalsausprägungen (genau 28 verschiedene Merkmalsausprägungen) auf, so dass eine Aufbereitung nach absoluten oder relativen Häufigkeitsverteilungen nicht zu mehr Übersicht beitragen würde. Hier bietet es sich an, Klassen zu bilden, um die Altersstruktur der Kunden besser zu verstehen. | |||
<!-- Tabelle Berechnung der notwendigen Größen --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
! style="text-align:left;" | Größe !! style="text-align:left;" | Formel !! style="text-align:left;" | im Beispiel mit !! style="text-align:left;" |Einsetzen und Berechnen | |||
|- | |||
| Klassenanzahl || <math>k \approx</math> \sqrt{n}</math> || <math>n=30</math> || <math>k \approx \sqrt{30}</math><math>\approx 5,8\approx 6</math> | |||
|- | |||
| Spannweite || <math>R=</math><math>x_{max}-x_{min}</math> || <math>x_{max}=75</math> und <math>x_{min}=4</math> || <math>R=</math><math>75-4=71</math> | |||
|- | |||
| Klassenbreite || <math>b=\frac{R}{k}</math> || <math>R=71</math> und <math>k=6</math> || <math>b=\frac{71}{\sqrt{30}}</math><math> \approx 13</math> | |||
|} | |||
</div> | |||
<!-- Ende Tabelle Berechnung der notwendigen Größen --> | |||
|- | |||
|colspan="6" |Jetzt geht es an die '''Klassenbildung''': | |||
Legt man fest, dass die '''untere Grenze''' selbst nicht zur Klasse gehört, aber die '''obere Grenze''' der Klasse dazugehört, so hat man sichergestellt, dass die Beobachtungswerte den Klassen eindeutig zugeordnet werden können. | |||
Dann wählt man einen '''Startwert''' für die untere Grenze der ersten Klasse <math>k_1</math> und addiert dann für die obere Klassengrenze die Klassenbreite zum Startwert. Die jeweils nächste Klasse hat dann als untere Grenze die obere Grenze der vorangegangenen Klasse. | |||
Wählt man den Startwert <math>0</math>, so erhält man die Klassen <math>k_i</math> mit <math>i=1;2;3;4;5;6</math>: | |||
:: <math>k_1=]0;13], k_2=]13;26], k_3=]26;39],</math> | |||
:: <math>k_1=]39;52], k_2=]52;65], k_3=]65;78]</math> | |||
|} | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<br /> | |||
<!-- Einführungsbeispiel - Teil 6.2 --> | |||
{|style="color: black; background-color: #FFFAFA;border-left:solid 2px #CD0000;border-right:solid 2px #CD0000;border-top:solid 2px #CD0000;border-bottom:solid 2px #CD0000;font-size:100%;font-size:100%;" | |||
|colspan="6" | | |||
<u>'''Einführungsbeispiel - Teil 6.2'''<br /></u> | |||
Jetzt muss die absolute Häufigkeit ermittelt werden, mit der die Beobachtungswerte in den einzelnen Klassen liegen: | |||
<!-- Tabelle Klassenbildung 1 --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
! colspan="3"| Klassen !! colspan="3"| Häufigkeiten | |||
|- | |||
| '''Klasse <math>k_i</math>'''|| '''über ... Jahre''' || '''bis zu ... Jahre''' || '''<math>H(k_i)</math>''' || '''<math>h(k_i)</math>''' || '''<math>h(k_i)</math> in Prozent''' | |||
|- | |||
|<math>k_1</math> || <math>0</math> || <math>13</math> || <math>5</math> || <math>\frac{1}{6}</math> || <math>16,7%</math> | |||
|- | |||
|<math>k_2</math> || <math>13</math> || <math>26</math> || <math>11</math> || <math>\frac{11}{30}</math> || <math>36,7%</math> | |||
|- | |||
|<math>k_3</math> || <math>26</math> || <math>39</math> || <math>4</math> || <math>\frac{2}{15}</math> || <math>13,3%</math> | |||
|- | |||
|<math>k_4</math> || <math>39</math> || <math>52</math> || <math>4</math> || <math>\frac{2}{15}</math> || <math>13,3%</math> | |||
|- | |||
|<math>k_5</math> || <math>52</math> || <math>65</math> || <math>3</math> || <math>\frac{1}{10}</math> || <math>10,0%</math> | |||
|- | |||
|<math>k_6</math> || <math>65</math> || <math>78</math> || <math>3</math> || <math>\frac{1}{10}</math> || <math>10,0%</math> | |||
|- | |||
! colspan="3"| Summe || align=left |<math>100</math> || align=left |<math>1</math> || align=left|<math>100%</math> | |||
|} | |||
</div> | |||
<!-- Ende Tabelle Klassenbildung 1 --> | |||
|- | |||
| colspan="6"| '''Interpretation''' | |||
Auffällig ist, dass mehr als ein Drittel aller Kunden zwischen 13 und 26 Jahren alt sind. Der Besitzer der Eisdiele könnte hieraus zum Beispiel ableiten, dass er mehr Angebote für die anderen Altersklassen anbieten sollte, um auch für diese Gruppen attraktiv zu sein und so mehr Umsatz zu erzielen. | |||
'''Ausblick''' | |||
Selbstverständlich wäre es auch möglich, eine andere Klassenanzahl zu wählen und so zu anderen Ergebnissen zu gelangen. Es ist nicht zwingend, die obigen Formeln für die Klassenanzahl und Klassenbreite zu wählen. Sie bieten aber einen guten Anhaltspunkt für eine erste Auswertung. | |||
Hier noch eine weitere Auswertung mit 8 Klassen und einer Klassenbreite von 10. | |||
<!-- Tabelle Klassenbildung 2 --> | |||
<div style="float:left; margin-right:1em;"> | |||
{| class="wikitable" | |||
! colspan="3"| Klassen !! colspan="3"| Häufigkeiten | |||
|- | |||
| '''Klasse <math>k_i</math>'''|| '''über ... Jahre''' || '''bis zu ... Jahre''' || '''<math>H(k_i)</math>''' || '''<math>h(k_i)</math>''' || '''<math>h(k_i)</math> in Prozent''' | |||
|- | |||
|<math>k_1</math> || <math>0</math> || <math>10</math> || <math>2</math> || <math>\frac{1}{6}</math> || <math>6,7%</math> | |||
|- | |||
|<math>k_2</math> || <math>10</math> || <math>20</math> || <math>10</math> || <math>\frac{1}{3}</math> || <math>33,3%</math> | |||
|- | |||
|<math>k_3</math> || <math>20</math> || <math>30</math> || <math>4</math> || <math>\frac{2}{15}</math> || <math>13,3%</math> | |||
|- | |||
|<math>k_4</math> || <math>30</math> || <math>40</math> || <math>5</math> || <math>\frac{1}{6}</math> || <math>16,7%</math> | |||
|- | |||
|<math>k_5</math> || <math>40</math> || <math>50</math> || <math>2</math> || <math>\frac{1}{15}</math> || <math>6,7%</math> | |||
|- | |||
|<math>k_6</math> || <math>50</math> || <math>60</math> || <math>3</math> || <math>\frac{1}{10}</math> || <math>10,0%</math> | |||
|- | |||
|<math>k_7</math> || <math>60</math> || <math>70</math> || <math>3</math> || <math>\frac{1}{10}</math> || <math>10,0%</math> | |||
|- | |||
|<math>k_8</math> || <math>70</math> || <math>80</math> || <math>1</math> || <math>\frac{1}{30}</math> || <math>3,3%</math> | |||
|- | |||
! colspan="3"| Summe || align=left |<math>100</math> || align=left |<math>1</math> || align=left|<math>100%</math> | |||
|} | |||
</div> | |||
<!-- Ende Tabelle Klassenbildung 2 --> | |||
|} | |||
<!-- Ende Einführungsbeispiel - Teil 6 --> | |||
Hier geht's weiter [[../Klassen mit unterschiedlicher Klassenbreite|Klassen mit unterschiedlicher Klassenbreite]] | Hier geht's weiter [[../Klassen mit unterschiedlicher Klassenbreite|Klassen mit unterschiedlicher Klassenbreite]] | ||
[[../|zurück zu Klassenbildung]] | [[../|zurück zu Klassenbildung]] | ||
[[../../|zurück zu Grundlagen der beschreibenden Statistik]] | [[../../|zurück zu Grundlagen der beschreibenden Statistik]] | ||
Version vom 7. April 2015, 22:07 Uhr
Für die Anzahl der Klassen gilt die folgende Regel,
wobei der Stichprobenumfang ist:
| Fortsetzung Beispiel Körpergröße (in cm)
Im Beispiel ist
Also gilt für die Anzahl der Klassen
|
Eine Klasse ist ein Teil der Spannweite ( für Range,dem englischen Begriff für Spannweite), also ein Teil der Differenz zwischen der größten Merkmalsausprägung und der kleinsten Merkmalsausprägung .
| Fortsetzung Beispiel Körpergröße (in cm)
Im Beispiel ist
somit gilt für die Spannweite
|
Die Klassenbreite ist der Quotient aus Spannweite und Klassenanzahl.
| Fortsetzung Beispiel Körpergröße (in cm)
Im Beispiel ist die Klassenbreite also . |
Bei der Zuordnung der Merkmalsausprägungen ist darauf zu achten, dass sich die Klassen nicht überschneiden. Sonst könnte es passieren, dass eine Merkmalsausprägung zwei Klassen zugeordnet wird.
Beachten Sie: Wählen Sie einen geeigneten Startwert als untere Klassengrenze (die in der Regel nicht zur Klasse gehören sollte) der ersten Klasse, addieren Sie die Klassenbreite um die obere Klassengrenze (diese gehört zur Klasse) zu erhalten.
Die obere Klassengrenze der vorangegangenen Klasse wird die untere Grenze der nächsten Klasse.
Und so fährt man fort, bis alle Klassen definiert sind.
Die einzelnen Klassen bezeichnet man mit , wobei gilt.
Klassenanzahl:
Spannweite:
Klassenbreite:
| Fortsetzung Beispiel Körpergröße (in cm)
Man bestimmt nun die fünf Klassen der Breite 10 und beachtet dabei, dass die Klassen sich nicht überschneiden dürfen. Dann bestimmt man die absoluten Häufigkeiten der einzelnen Klassen, dabei werden alle Merkmalsausprägungen gezählt, die zu der jeweiligen Klasse gehören. Dann berechnet man die relativen Häufigkeiten der einzelnen Klassen.
| |||||||||||||||||||||||||||||||||||
|
Diese Darstellung ist zunächst eher objektiv und der Leser der Tabelle wird nicht in die Irre geleitet. Festzuhalten ist, das es sich um eine Klasse mit eher großen Schülern handelt. | |||||||||||||||||||||||||||||||||||
|
Einführungsbeispiel - Teil 6.1 Bei der Umfrage der Eisdiele "Rabe" weist das Merkmal "Alter" sehr viele verschiedene Merkmalsausprägungen (genau 28 verschiedene Merkmalsausprägungen) auf, so dass eine Aufbereitung nach absoluten oder relativen Häufigkeitsverteilungen nicht zu mehr Übersicht beitragen würde. Hier bietet es sich an, Klassen zu bilden, um die Altersstruktur der Kunden besser zu verstehen.
| |||||||||||||||||||
| Jetzt geht es an die Klassenbildung:
Legt man fest, dass die untere Grenze selbst nicht zur Klasse gehört, aber die obere Grenze der Klasse dazugehört, so hat man sichergestellt, dass die Beobachtungswerte den Klassen eindeutig zugeordnet werden können. Dann wählt man einen Startwert für die untere Grenze der ersten Klasse und addiert dann für die obere Klassengrenze die Klassenbreite zum Startwert. Die jeweils nächste Klasse hat dann als untere Grenze die obere Grenze der vorangegangenen Klasse. Wählt man den Startwert , so erhält man die Klassen mit : | |||||||||||||||||||
|
Einführungsbeispiel - Teil 6.2 Jetzt muss die absolute Häufigkeit ermittelt werden, mit der die Beobachtungswerte in den einzelnen Klassen liegen:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Interpretation
Auffällig ist, dass mehr als ein Drittel aller Kunden zwischen 13 und 26 Jahren alt sind. Der Besitzer der Eisdiele könnte hieraus zum Beispiel ableiten, dass er mehr Angebote für die anderen Altersklassen anbieten sollte, um auch für diese Gruppen attraktiv zu sein und so mehr Umsatz zu erzielen. Ausblick Selbstverständlich wäre es auch möglich, eine andere Klassenanzahl zu wählen und so zu anderen Ergebnissen zu gelangen. Es ist nicht zwingend, die obigen Formeln für die Klassenanzahl und Klassenbreite zu wählen. Sie bieten aber einen guten Anhaltspunkt für eine erste Auswertung. Hier noch eine weitere Auswertung mit 8 Klassen und einer Klassenbreite von 10.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hier geht's weiter Klassen mit unterschiedlicher Klassenbreite