Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Quadratische Funktionen erforschen/Wiederholung (Optional): Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Elena Jedtke KKeine Bearbeitungszusammenfassung |
Main>Elena Jedtke KKeine Bearbeitungszusammenfassung |
||
| Zeile 25: | Zeile 25: | ||
<iframe src="//LearningApps.org/watch?v=p563afae517" style="border:0px;width:80%;height:500px" webkitallowfullscreen="false" mozallowfullscreen="true"></iframe> | <iframe src="//LearningApps.org/watch?v=p563afae517" style="border:0px;width:80%;height:500px" webkitallowfullscreen="false" mozallowfullscreen="true"></iframe> | ||
'''b)''' Überlege dir eine Begründung für die richtige | '''b)''' Überlege dir eine Begründung für die richtige Darstellung der Entfernung zum Startpunkt.}} | ||
Version vom 31. August 2017, 12:24 Uhr
| Bevor du loslegst, dich in das neue Thema Quadratische Funktionen einzuarbeiten, kannst du auf dieser Seite dein bisheriges Wissen über Funktionen auffrischen. |
Teste dein Wissen über (lineare) Funktionen
Aufgabe
{{{1}}}
Graphen zu einer Sachsituation
Aufgabe
Zeigt der Graph einen funktionalen Zusammenhang?
Aufgabe
Videos und Merksätze
Daniel Jung hat auf Youtube in seinem Channel Mathe by Daniel Jung zu den verschiedensten Themen Erklärvideos erstellt. Hier kannst du dir Videos zu dem Thema Was ist eine Funktion? bzw. eine Übersicht über Lineare Funktionen anschauen. Denke daran dir Kopfhörer anzuziehen, sofern du nicht alleine in einem Raum bist.
Merke
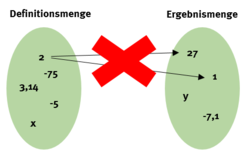
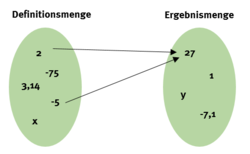
- Eine Funktion ordnet jedem Element einer Ausgangsmenge (Definitionsmenge) genau ein Element der Zielmenge (Ergebnismenge) zu. Ein Element aus der Ergebnismenge kann mehreren Elementen der Definitionsmenge zugeordnet werden.
- Lineare Funktionen liegen in der Form vor, wobei m die Steigung der Geraden und b den y-Achsenabschnitt angibt.
- Funktionen mit dem Term nennt man proportionale Funktionen. Sie sind ein Spezialfall der linearen Funktionen.
Erstellt von: Elena Jedtke (Diskussion)