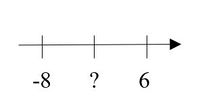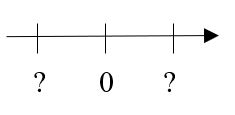Einführung in die Negativen Zahlen/Erweiterung der Zahlengeraden: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 10: | Zeile 10: | ||
{{Box | {{Box | ||
|Titel= Frage | |Titel= Frage | ||
|Inhalt= Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null? | |Inhalt= Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null? | ||
| | |Klasse=Frage | ||
}} | }} | ||
Aktuelle Version vom 18. Februar 2024, 23:14 Uhr
Findet zu jeder Situation eine passende ganze Zahl. Ordnet die Situation an die richtige Stelle auf der Zahlengeraden.
Von den beiden folgenden Aufgaben könnt ihr eine auswählen. Die linke Aufgabe ist etwas leichter als die rechte Aufgabe. Für beide Aufgaben könnt ihr die Zahlengerade benutzen.
(Die Sternchen-Aufgaben sind schwerer als die anderen.)
a) 7 und 17
b) -8 und 0
c) -8 und 12
d) -2 und 6
*e) -100 und -36
*f) -28 und 12
Entgegengesetzte Zahlen und Betrag
- Lest euch das Merkekästchen gut durch.
- Löst die Aufgaben in den Learning Apps.
- Notiert auf eurem Protokoll drei Beispiele zu entgegengesetzten Zahlen und zwei Beispiele zum Betrag. Ihr könnt Beispiele aus den Aufgaben nehmen.
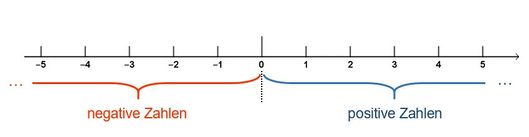
- Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen entgegengesetzte Zahlen.
- Der Abstand einer Zahl zur 0 heißt Betrag und wird mit Betragsstrichen gekennzeichnet, z.B. |-4| = 4; |+4| = 4.
Weitere Erklärungen zum Betrag
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann. Der Betrag der 0 ist 0, da man ja keine Schritte mehr laufen muss, um zur 0 zu gelangen.