Einführung in die Automatentheorie/4. Stunde: Unterschied zwischen den Versionen
K (7 Versionen importiert) |
(formatiert) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 64: | Zeile 64: | ||
L={(hah)<sup>n</sup> !<sup>2</sup>)<math>\| n\ >0</math>} }} | L={(hah)<sup>n</sup> !<sup>2</sup>)<math>\| n\ >0</math>} }} | ||
{{Aufgaben|1=4.6|2=Öffne mittels Jflap die Datei A45.jff und ändere sie ab, so dass der Automat nur noch die Sprache L={(hi)<sup>n</sup> !)<math>\| n\geq0</math>} | {{Aufgaben|1=4.6|2=Öffne mittels Jflap die Datei A45.jff und ändere sie ab, so dass der Automat nur noch die Sprache L={(hi)<sup>n</sup> !)<math>\| n\geq0</math>} akzeptiert. }} | ||
Aktuelle Version vom 10. August 2019, 12:53 Uhr
Java Formal Language & Automata Package (kurz: Jflap)
Nun wollen wir uns mit der Simulation von Automaten beschäftigen.
Das Programm Jflap gibt uns unter anderem die Möglichkeit Automaten zu entwerfen
und ihr Akzeptanzverhalten zu testen. Im folgenden Beispiel lernst du Jflap
selber zu bedienen. Damit du dies lernst, vollziehe die im Beispiel beschriebenen
Schritte selber nach!
- Als erstes startest du Jflap! Wenn du dabei Probleme hast, frag einfach deinen Lehrer!
- Nach dem Start von Jflap erscheint zunächst ein Fenster, in dem man die Art des Automaten auswählen kann.

- Wir beschäftigen uns erstmal nur mit endlichen Automaten, deswegen wählen wir ”Finite Automaton“ (deutsch: endlicher Automat). Nun erscheint ein weiteres Fenster zur Erstellung des Automaten.
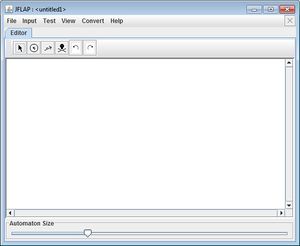
Links oben siehst du mehrere Symbole. ![]()
 Mauspfeil
Mauspfeil
Zum Verschieben der Zustände und zum Setzen von Zuständen mit Hilfe der rechten Maustaste als Start- bzw. Endzustand (Initial bzw. Final).
 Kreis mit einem q in der Mitte
Kreis mit einem q in der Mitte
Zum setzen von Zuständen mit automatischen Bezeichnungen von q0, q1, ... (im Jflap werden die Zustände mit dem Buchstaben q bezeichnet.)
 Langezogenen Pfeil
Langezogenen Pfeil
Durch Drücken der linken Maustaste auf den Anfangszustand und Loslassen der Taste am Endzustand wird ein Übergang gesetzt. In das sich öffnende Fenster kann das Eingabezeichen eingegeben werden.
Testen auf Korrektheit
Konstruiere mittels Jflap einen Akzeptor, der folgende Sprache akzeptiert:
L={(ab)n} L={(ba)n}
Hinweis: Die Vereinigungsmenge wird hier als oder interpretiert.
Jetzt wollen wir das Verhalten des Automaten testen. Jflap bietet uns dafür zwei Möglichkeiten:
- 1. Möglichkeit:
Der Automat arbeitet das Wort schrittweise ab.
Gehe dazu in der Menübar des bereits geöffneten Fensters mit dem Automaten auf Input -> Step by State. Es erscheint ein Eingabefenster. Gebe dort die Eingabe abababab ein. Ein weiteres Fenster öffnet sich. Hier kannst du das Verhalten des Automaten schrittweise nachvollziehen, indem du auf Step klickst. Um den Automaten erneut mit der gleichen Eingabe zu starten, musst du Reset drücken. Starte nun auf gleiche Weise den Automaten einmal mit der Eingabe ba und einmal mit der Eingabe bab. Dabei siehst du, dass auf die Eingabe ba sich der Automat grün färbt, die Eingabe wird also akzeptiert. Die Eingabe bab kann der Automat allerdings nicht verarbeiten, deswegen stoppt er an der Stelle, wo das Wort abgearbeitet ist, egal wie oft Step jetzt noch gedrückt wird.
- 2. Möglichkeit:
Es werden mehrere Eingaben gleichzeitig getestet. Gehe dazu auf Input -> Multiple Run. Das Fenster wird in zwei Fenster geteilt. Auf der linken Seite siehst du weiterhin deinen Automaten. Auf der rechten Seite erscheint eine Input und eine Result Spalte. In der Input Spalte kannst du nun untereinander mehrere Eingaben eingeben. Jede Eingabe beendest du dabei mit einem Return. Gebe nun in die Input Spalte die Eingaben ab, ababab, ababa, ba, baba und babab ein. Durch klicken auf Run Inputs werden deine Eingaben ausgewertet. Die Auswertung, ob dein Automat die Eingaben akzeptiert oder nicht, kannst du in der Result Spalte ablesen. Steht dort ein Accept (deutsch: akzeptieren), so akzeptiert der Automat die entsprechende Eingabe. Steht dort ein Reject (deutsch: verwerfen = nicht akzeptieren), so akzeptiert der Automat die Eingabe nicht.
Übungen mittels Jflap
Bearbeite die folgenden Aufgaben und speichere sie jeweils unter der Aufgabennummer wie bei Aufgabe 4.1.
Teste jeweils wie oben beschrieben deinen Automaten auf Korrektheit.
Konstruiere einen Akzeptor, der nur die folgende Sprache akzeptiert:
L={(anb2)}
Konstruiere einen Akzeptor, der nur die folgende Sprache akzeptiert:
L={(anb2)}
Konstruiere einen Akzeptor, der nur die folgende Sprache akzeptiert:
L={(hah)n !2)}



