Zentrische Streckung/Eigenschaften der zentrischen Streckung/4.Station: Unterschied zwischen den Versionen
Main>Leonie Porzelt (Panto eingefügt) |
Keine Bearbeitungszusammenfassung |
||
| (30 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken | |||
|{{Eigenschaften der zentrischen Streckung}} | |||
|Lernschritte einblenden | |||
|Lernschritte ausblenden | |||
}} | |||
__NOTOC__ | |||
==4. Station: Längenverhältnistreue== | ==4. Station: Längenverhältnistreue== | ||
[[Bild:Porzelt_lobenderDia3.jpg]] | |||
[[Bild:Porzelt_Panto-2.jpg| | |||
{{Box|1=Definition Längenverhältnistreue|2= | |||
[[Bild:Porzelt_Panto-2.jpg|right]] | |||
'''Längenverhältnistreue''' liegt vor, wenn das Längenverhältnis von zwei Bildstrecken gleich dem Längenverhältnis der beiden Urstrecken ist. | |||
|3=Merksatz}} | |||
{{Box|1=Finde heraus ob eine zentrische Streckung längenverhältnistreu ist!|2= | |||
[[Bild:Porzelt_Verhältnistreu.jpg|right]] | |||
'''Arbeitsauftrag:''' | |||
#Berechne den Streckungsfaktor k.<br> | |||
#Berechne <math>\overline{A'P'}</math> und <math>\overline{P'B'}</math>. (Tipp: Beim Eintragen Leerzeichen zwischen Zahl und Einheit nicht vergessen!) | |||
#Berechne <math>{\overline{AP}\over\overline{PB}}</math> und <math>{\overline{A'P'}\over\overline{P'B'}}</math>. Runde auf 2 Nachkommastellen. | |||
<br> | <br> | ||
Mit Hilfe der folgenden Lückentexte kannst du den Arbeitsauftrag lösen.<br> | |||
Denk konzentriert nach und setze die richtige Aussage in die passende Lücke ein, um die Ergebnisse berechnen zu können:<br> | |||
'''Zu Punkt 1:'''<br> | |||
<div class="lueckentext-quiz"> | |||
<math>\mid k \mid</math> = '''<math>\overline{ZB'}</math>''' : '''<math>\overline{ZB}</math>'''<br> | |||
Einsetzen der Werte:<br> | |||
<math>\mid k \mid</math> = '''6''' : '''3''' = '''2 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | |||
</div> | </div> | ||
'''Zu Punkt 2:'''<br> | |||
<div class="lueckentext-quiz"> | |||
[[Bild:Porzelt_Verhältnistreu.jpg|right]] | |||
<math>\overline{A'P'}</math> = '''<math>\mid k \mid</math>''' <math>\cdot</math> '''<math>\overline{AP}</math>'''<br> | |||
Einsetzen der Werte:<br> | |||
<math>\overline{A'P'}</math> = '''2''' <math>\cdot</math> '''0,7 cm''' = '''1,4 cm (Berechne das Ergebnis mit dem Taschenrechner und gib die Einheit mit an!)'''<br> | |||
<br> | <br> | ||
< | <math>\overline{P'B'}</math> = '''<math>\mid k \mid</math>''' <math>\cdot</math> '''<math>\overline{PB}</math>'''<br> | ||
{ | Einsetzen der Werte:<br> | ||
<math>\overline{P'B'}</math> = '''2''' <math>\cdot</math> '''1,5 cm''' = '''3 cm (Berechne das Ergebnis mit dem Taschenrechner und gib die Einheit mit an!)'''<br> | |||
<br> | |||
<br> | |||
</div> | </div> | ||
'''Zu Punkt 3:'''<br> | |||
- | <div class="lueckentext-quiz"> | ||
[[Bild:Porzelt_Verhältnistreu.jpg|right]] | |||
Entnehme dem Bild die Werte, berechne und runde das Ergebnis auf zwei Nachkommastellen:<br> | |||
{'''<math>{\overline{A'P'} | <math>\frac{\overline{AP}}{\overline{PB}}</math> = '''<math>\frac{0,7 cm}{1,5 cm}</math>''' = '''0,47 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | ||
<math>\frac{\overline{A'P'}}{\overline{P'B'}}</math> = '''<math>\frac{1,4 cm}{3 cm}</math>''' = '''0,47 (Berechne das Ergebnis mit dem Taschenrechner)'''<br> | |||
</div> | |||
|3=Arbeitsmethode}} | |||
<br> | <br> | ||
[[Bild:Porzelt_lobenderPanto6.jpg]] | |||
<br> | |||
{{Box|1=Wie erklärt sich die Gleichheit in Punkt 3 aus der vorherigen Aufgabe?|2= | |||
[[Bild:Porzelt_fragenderDia-1.jpg|right]] | |||
Warum ist das Längenverhältnis von <math>\overline{AP}</math> und <math>\overline{PB}</math> gleich dem Längenverhältnis der Bildstrecken? | |||
Warum ist <math>{\overline{AP}\over\overline{PB}}</math> = <math>{\overline{A'P'}\over\overline{P'B'}}</math>? | |||
|3=Frage}} | |||
{{Box|1=Finde die Antwort auf die Frage!|2= | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Für <math>\overline{ | Für <math>\overline{A'P'}</math> kann man auch '''<math>\mid k\mid \cdot \overline{AP}</math>''' und für <math>\overline{P'B'}</math> kann man '''<math>\mid k\mid \cdot \overline{PB}</math>''' einsetzen. <br> | ||
Daraus folgt: <math>{\overline{ | Daraus folgt: <math>{\overline{A'P'}\over\overline{P'B'}} ={{|k|}\over{|k|}}\cdot</math> '''<math>{\overline{AP}\over\overline{PB}}</math>'''.<br> | ||
<math>\mid k\mid</math> kann man rauskürzen, so dass '''<math>{\overline{A'P'}\over\overline{P'B'}}</math>''' <math>= {\overline{AP}\over\overline{PB}}</math> gilt. | |||
</div> | </div> | ||
|3=Lösung}} | |||
<br> | |||
[[Bild:Porzelt_lobenderDia5.jpg]] | |||
<br> | <br> | ||
{{Box|1=Gelten die Überlegungen für alle Strecken?|2= | |||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
'''Ist die zentrische Streckung längenverhältnistreu?''' | '''Ist die zentrische Streckung längenverhältnistreu?''' | ||
(Ja) (!Nein) | (Ja) (!Nein) | ||
</div> | </div> | ||
|3=Frage}} | |||
{{Fortsetzung|weiter=Kreistreue|weiterlink=../5.Station}} | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 15:58 Uhr
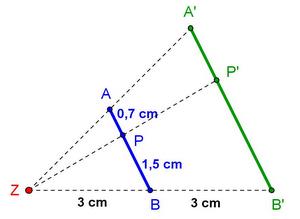
4. Station: Längenverhältnistreue
Arbeitsauftrag:
- Berechne den Streckungsfaktor k.
- Berechne und . (Tipp: Beim Eintragen Leerzeichen zwischen Zahl und Einheit nicht vergessen!)
- Berechne und . Runde auf 2 Nachkommastellen.
Mit Hilfe der folgenden Lückentexte kannst du den Arbeitsauftrag lösen.
Denk konzentriert nach und setze die richtige Aussage in die passende Lücke ein, um die Ergebnisse berechnen zu können:
Zu Punkt 1:
= :
Einsetzen der Werte:
= 6 : 3 = 2 (Berechne das Ergebnis mit dem Taschenrechner)
Zu Punkt 2:
=
Einsetzen der Werte:
= 2 0,7 cm = 1,4 cm (Berechne das Ergebnis mit dem Taschenrechner und gib die Einheit mit an!)
=
Einsetzen der Werte:
= 2 1,5 cm = 3 cm (Berechne das Ergebnis mit dem Taschenrechner und gib die Einheit mit an!)
Zu Punkt 3:
Für kann man auch und für kann man einsetzen.
Daraus folgt: .
kann man rauskürzen, so dass gilt.
Ist die zentrische Streckung längenverhältnistreu? (Ja) (!Nein)