Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Zentrische Streckung/Eigenschaften der zentrischen Streckung/3.Station: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Leonie Porzelt KKeine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (34 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken | |||
|{{Eigenschaften der zentrischen Streckung}} | |||
|Lernschritte einblenden | |||
|Lernschritte ausblenden | |||
}} | |||
__NOTOC__ | |||
==3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue== | ==3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue== | ||
< | [[Bild:Porzelt_sofa.jpg]] | ||
<br><br> | |||
{{Box|1=Definition der Winkeltreue, der Längentreue und der Flächeninhaltstreue|2= | |||
[[Bild:Porzelt_Panto-2.jpg|right]] | |||
'''Winkeltreue''' liegt vor, wenn alle Bildwinkel genauso groß sind wie die Urbildwinkel. | |||
<br><br> | |||
Ebenso gilt für die '''Längentreue''', dass alle Bildstrecken genauso lang sind wie die Urbildstrecken. | |||
<br><br> | |||
'''Flächeninhaltstreue''' liegt vor, wenn der Flächeninhalt des Bildes genauso groß ist wie der Flächeninhalt des Urbildes. | |||
|3=Merksatz}} | |||
{{Box|1=Graphische Veranschaulichung der drei Begriffe|2= | |||
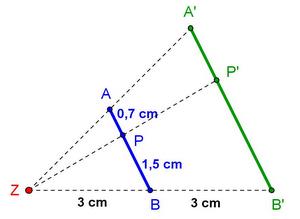
In diesem Applet siehst du ein Dreieck, das um den Faktor k = 3,5 zentrisch gestreckt wurde. Lass dir das Winkelmaß, die Streckenlängen und den Flächeninhalt anzeigen! <br> | |||
<ggb_applet height="400" width="750" showResetIcon="true" id="w64dafer" /> | |||
Vergleiche die Werte und überlege, welche Eigenschaften zutreffen! | |||
<br> | <br> | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| Zeile 22: | Zeile 32: | ||
(Winkeltreue) (!Längentreue) (!Flächeninhaltstreue) | (Winkeltreue) (!Längentreue) (!Flächeninhaltstreue) | ||
</div> | </div> | ||
|3=Arbeitsmethode}} | |||
:Nur wie kann man jetzt den Flächeninhalt des zentrisch gestreckten Dreiecks berechnen? | |||
{{Box|1=Wie berechne ich den Flächeninhalt des gestreckten Dreiecks?|2= | |||
[[Bild:Porzelt_fragenderDia-1.jpg|right]] | |||
Nur - wie kann man jetzt den Flächeninhalt des zentrisch gestreckten Dreiecks berechnen? Finde es durch Umformung heraus! Setze dafür die richtige Aussage in die passende Lücke ein: | |||
<br><br> | |||
<div class="grid"> | |||
<div class="width-1-4"> | |||
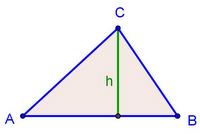
[[Bild:Porzelt_Dreiecke.jpg|thumb|300px|right|Flächeninhalt: A = 0.5 ∙ <span style="text-decoration: overline;">AB</span> ∙ h]] | |||
</div> | |||
<div class="width-3-4"> | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
<math>A_{\Delta ABC} = 0.5 \cdot \overline{AB} \cdot h </math><br> | |||
<math>A_{\Delta A'B'C'} = 0.5 \cdot \overline{A'B'} \cdot h' </math><br> | |||
<math>A_{\Delta A'B'C'} = 0.5 \cdot \vert k \vert \cdot</math> '''<math>\overline{AB}</math>''' <math> \cdot \vert k \vert \cdot </math> '''<math> h </math>''' <br> | |||
<math>A_{\Delta A'B'C'} =</math> '''<math> \vert k \vert ^2</math>''' <math>\cdot 0.5 \cdot \overline{AB} \cdot h </math><br> | |||
<math>A_{\Delta A'B'C'} =</math> '''<math> \vert k \vert ^2 </math>''' <math> \cdot </math> '''<math> A_{\Delta ABC}</math>''' | |||
</div> | |||
</div> | |||
</div> | </div> | ||
|} | |||
|3=Arbeitsmethode}} | |||
[[Bild:Porzelt_lobenderDia2.jpg]] | |||
{{Fortsetzung|weiter=Längenverhältnistreue|weiterlink=../4.Station}} | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:GeoGebra]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 15:58 Uhr
3. Station: Winkeltreue, Längentreue und Flächeninhaltstreue
Definition der Winkeltreue, der Längentreue und der Flächeninhaltstreue
Graphische Veranschaulichung der drei Begriffe
In diesem Applet siehst du ein Dreieck, das um den Faktor k = 3,5 zentrisch gestreckt wurde. Lass dir das Winkelmaß, die Streckenlängen und den Flächeninhalt anzeigen!

Vergleiche die Werte und überlege, welche Eigenschaften zutreffen!
Welche Eigenschaften treffen auf die zentrische Streckung zu? (Winkeltreue) (!Längentreue) (!Flächeninhaltstreue)
Wie berechne ich den Flächeninhalt des gestreckten Dreiecks?