Lineare Funktionen im Aktiv-Urlaub/Wertetabelle und Funktionsgleichung: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
(linkfix) Markierung: 2017-Quelltext-Bearbeitung |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Lineare Funktionen im Aktiv-Urlaub}} | |||
{{ | |||
==2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung== | ==2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung== | ||
| Zeile 176: | Zeile 170: | ||
|Tipps|Verbergen}} | |Tipps|Verbergen}} | ||
{{Fortsetzung|vorher=2.2) Funktionsgleichung und Funktionsgraph|vorherlink=Lineare Funktionen im Aktiv-Urlaub/ | {{Fortsetzung|vorher=2.2) Funktionsgleichung und Funktionsgraph|vorherlink=Lineare Funktionen im Aktiv-Urlaub/Funktionsgleichung und Funktionsgraph|weiter=2.4) Lineare Funktionen im Aktiv-Urlaub und andere Anwendungen|weiterlink=Lineare Funktionen im Aktiv-Urlaub/Anwendungen}} | ||
Aktuelle Version vom 22. Mai 2022, 10:58 Uhr
0) Vorwissen zum Thema
1) Zuordnungen und Funktionen
2.1) Lineare Funktionen erkennen und darstellen
2.2) Funktionsgleichung und Funktionsgraph
2.3) Wertetabelle und Funktionsgleichung
2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung
Wiederholung: Erstellen einer Wertetabelle mithilfe der Funktionsgleichung
Du hast in den Einführungsbeispielen schon Wertetabellen erstellt. Schauen wir uns das Beispiel zum Bootsverleih noch einmal an. Die Funktionsgleichung lautet f(x) = 2x + 5
Um nun eine Wertetabelle zu erstellen, setze für x verschiedene Werte ein und berechne den zugehörigen y-Wert, den Funktionswert. Erinnerung: Werte von Termen berechnen (7. Klasse)
Das Video fasst das Vorgehen noch einmal zusammen:
Erstelle eine Wertetabelle zu
- f(x) = 2,5x
- f(x) = -2x - 1
Gib die Funktionsgleichungen bei GeoGebra ein und prüfe, ob die von dir errechneten Punkte auf dem Graphen der Funktion liegen.
https://www.geogebra.org/graphing
Punktprobe: Liegt der Punkt auf der Geraden?
Sie leihen für 3 Stunden ein Tretboot. Der Bootsverleiher rechnet den Preis 10€ aus.
Kann das sein?
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt.
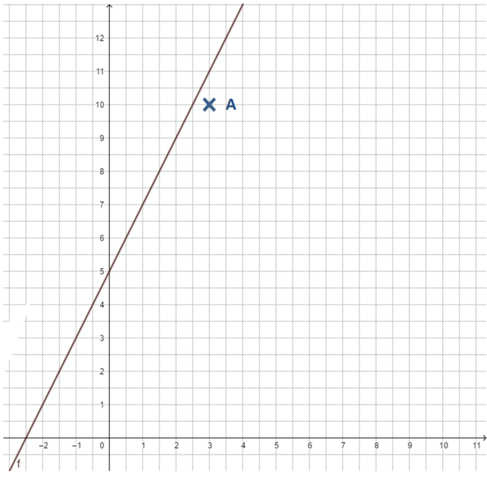
geg: Punkt A(3|10); Funktion f(x) = 2x + 5
ges: Liegt der Punkt A auf dem Graphen der Funktion?
In der Zeichnung erkennen wir sofort, dass dies nicht der Fall ist.
_%3D_2x_%2B_5_Punkt_A_liegt_nicht_auf_dem_Graphen.png)
Wie können wir rechnerisch prüfen, ob ein Punkt auf dem Graphen der Funktion liegt?
Schreibe die nachfolgende Rechnung in dein Heft.Gegeben ist die Funktionsgleichung y = 2x + 5. Liegt der Punkt A(3|10) auf dem Graphen der Funktion?
(Hier ist es leichter y statt f(x) zu schreiben, der Zusammenhang zu den Koordinaten des Punktes sind dann leichter zu erkennen.)
Idee: Setze die Koordinaten des Punktes in die Funktionsgleichung ein und prüfe, ob die Gleichung erfüllt wird.
y= 2x + 5 A(3|10)
10 = 2·3 + 5
10 = 6 + 5
10 = 11 (f)
Es ergibt sich eine falsche Aussage, die Gleichung ist nicht erfüllt, also liegt der Punkt nicht auf dem Graphen. Wir prüfen ebenso, ob der Punkt B(4|13) auf der Geraden liegt:
Punktprobe:
y = 2x + 5 B(4|13)
13 = 2·4 + 5
13 = 8 + 5
13 = 13 (w)
Es ergibt sich eine wahre Aussage, die Gleichung ist erfüllt, also liegt der Punkt auf dem Graphen.
Das folgende Video fasst noch einmal zusammen:
Fehlende Koordinate eines Punktes der Funktion berechnen
Tom und Lisa leihen ein Tretboot für 1,5 Stunden.
a) Wie viel müssen sie bezahlen?
Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen.
1. Möglichkeit: x-Koordinate ist gegeben
geg: x = 1,5 und f(x) = 2x+5
ges: zugehöriger y-Wert
Setze die x-Koordinate in die Funktionsgleichung ein und berechne: f(x) = 2x + 5
y = 2·1,5 + 5
= 3 + 5
= 8 P(1,5|8)
Sie müssen 8€ bezahlen.
2. Möglichkeit: y-Koordinate ist gegeben:
Tom und Lisa bezahlen 10 €. Wie lange haben sie das Tretboot ausgeliehen?
geg: y = 10 und f(x) = 2x+5
ges: zugehörige x-Koordinate
Setze die y-Koordinate in die Funktionsgleichung ein und löse nach x auf:
f(x) = 2x + 5
10 = 2x + 5 |-5
5 = 2x |:2
2,5 = x P(2,5|10)
Sie haben das Boot für 2,5 Stunden geliehen.
Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben
Bestimme die Funktionsgleichung.
Wenn die Gerade parallel zur Geraden von f(x)= 2x + 1 verläuft, haben die Geraden dieselbe Steigung! Also ist m = 2 gegeben. Außerdem hast du den Punkt P(1|5) gegeben. Gesucht ist b.
Setze die gegebenen Größen ein und löse nach b auf.
Schnittpunkte mit den Koordinatenachsen bestimmen
Nach welcher Zeit ist der Pool leer?
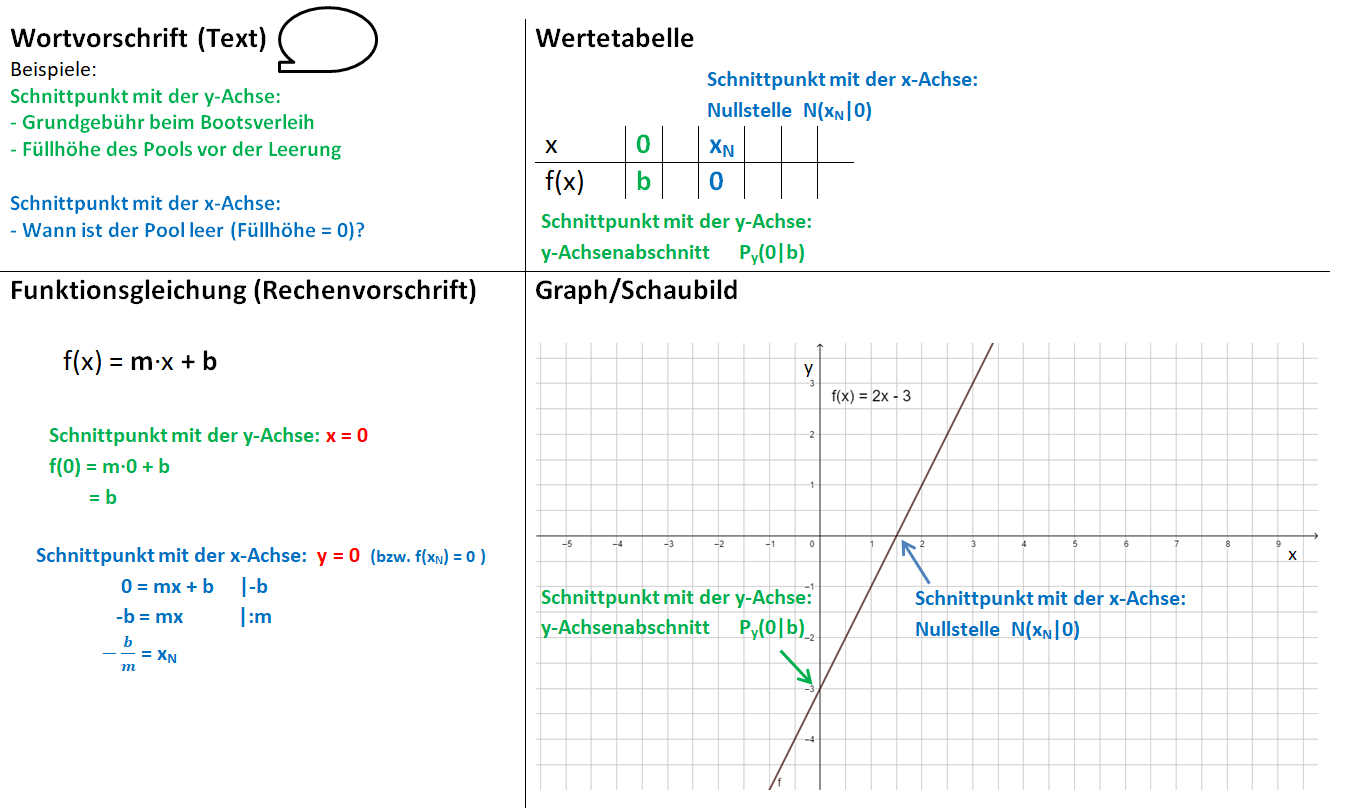
Für den Schnittpunkt Py mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b.
Py (0|b)
Für den Schnittpunkt N mit der x-Achse (Nullstelle) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf.
N (xNI0)
Bestimme die Schnittpunkte mit den Koordinatenachsen.
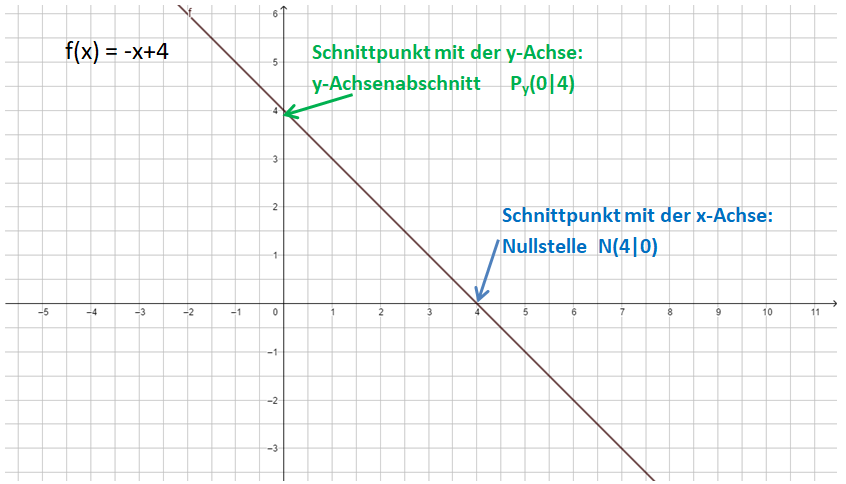
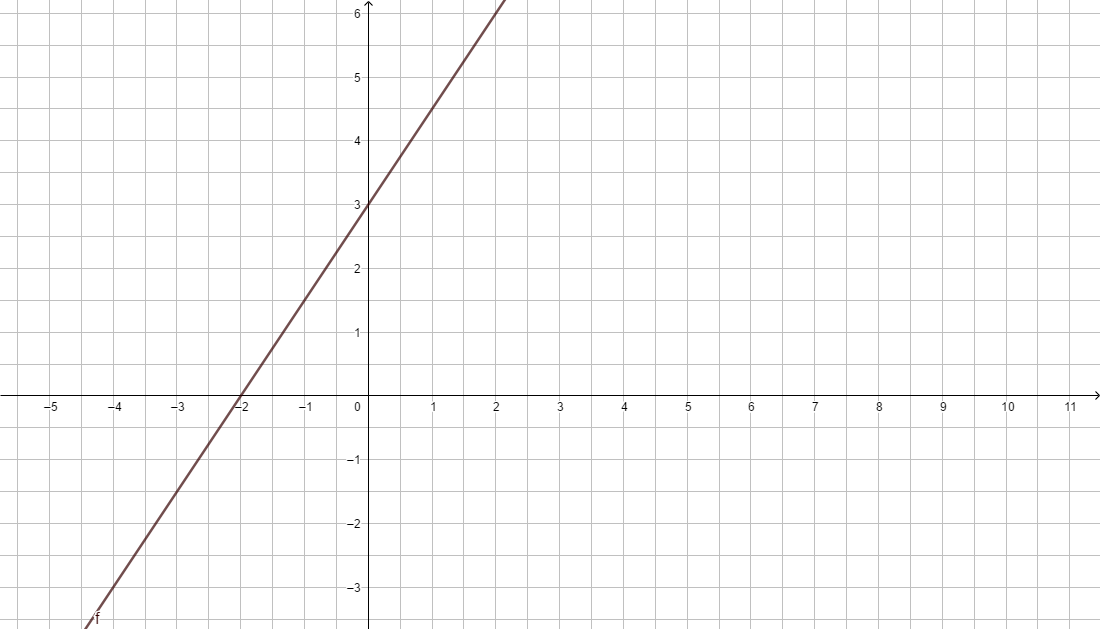
a) f(x) = -x+4
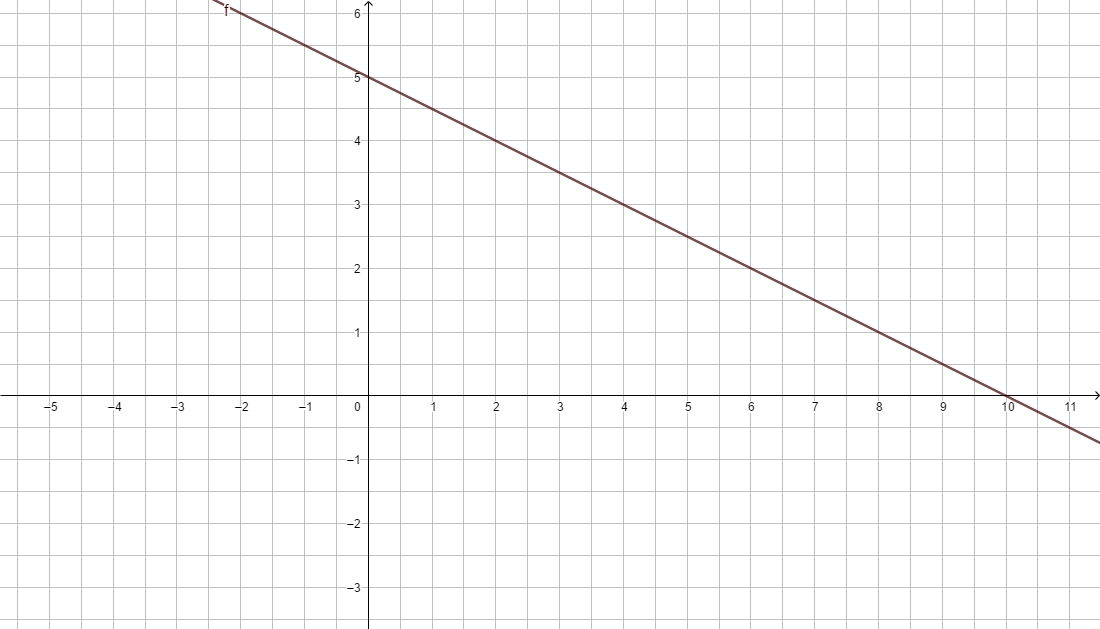
b) f(x) = -0,5x + 5
Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0
y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4
_%3D_-x%2B4_Schnittpunkte_mit_den_Koordinatenachsen.png)
_%3D_-0.5x%2B5.png)
_%3D_1.5x%2B3.png)
