Lineare Funktionen im Aktiv-Urlaub/Funktionsgleichung und Funktionsgraph: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (linkfix) Markierung: Quelltext-Bearbeitung 2017 |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{ | {{Lineare Funktionen im Aktiv-Urlaub}} | ||
==Wertetabelle und Funktionsgraph== | ==Wertetabelle und Funktionsgraph== | ||
| Zeile 365: | Zeile 359: | ||
{{Box|1=Übung 17|2=Gib die Funktionsgleichung an, die zur Geraden gehört. Notiere deine Lösung übersichtlich im Heft. Löse anschließend die | {{Box|1=Übung 17|2=Gib die Funktionsgleichung an, die zur Geraden gehört. Notiere deine Lösung übersichtlich im Heft. Löse anschließend die App unten.|3=Üben}} | ||
<div class="grid"> | <div class="grid"> | ||
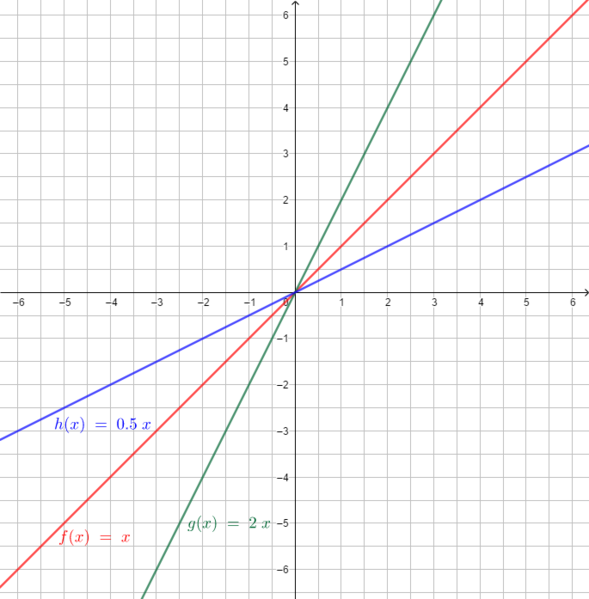
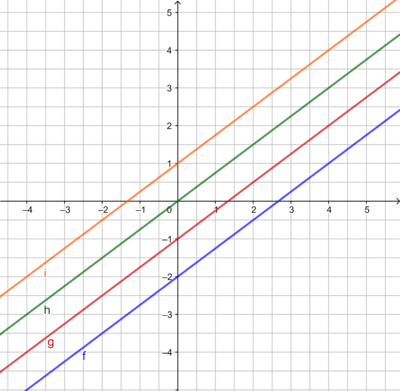
<div class="width-1-2">[[Datei:Parallele Geraden neu.png|rahmenlos|400x400px]] <br> | <div class="width-1-2">[[Datei:Parallele Geraden neu.png|rahmenlos|400x400px]] <br> | ||
| Zeile 372: | Zeile 365: | ||
g(x) = ...<br> | g(x) = ...<br> | ||
h(x) = ...<br> | h(x) = ...<br> | ||
i(x) = ...</div> | i(x) = ...<br> | ||
{{Lösung versteckt|1=Öffne das GeoGebra-Applet und verändere den Wert des Schiebereglers b.<br> | |||
<ggb_applet id="kykz4qcf" width="1051" height="572" border="888888" />|2=Tipp|3=Verbergen}}</div> | |||
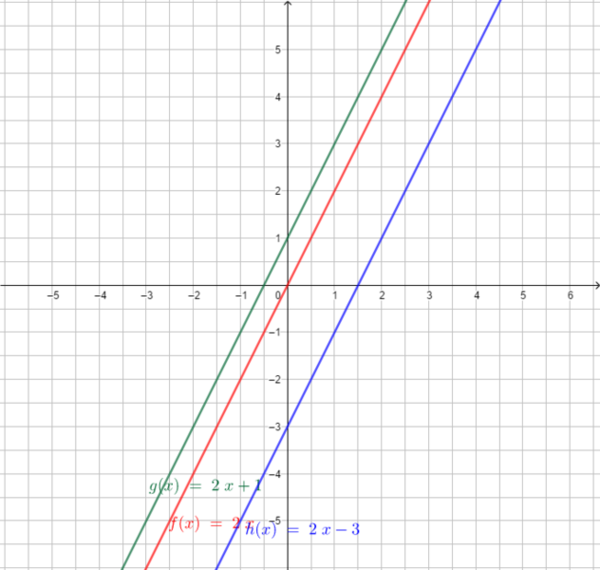
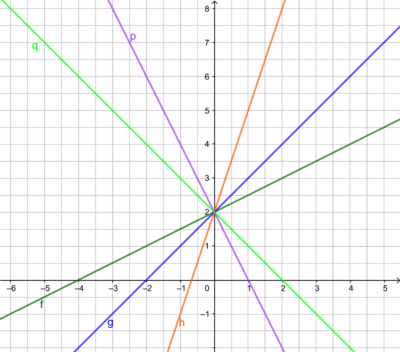
<div class="width-1-2">[[Datei:Geraden mit b=2.png|rahmenlos|400x400px]]<br> | <div class="width-1-2">[[Datei:Geraden mit b=2.png|rahmenlos|400x400px]]<br> | ||
f(x) = ...<br> | f(x) = ...<br> | ||
| Zeile 378: | Zeile 373: | ||
h(x) = ...<br> | h(x) = ...<br> | ||
p(x) = ...<br> | p(x) = ...<br> | ||
q(x) = ...<br> | q(x) = ...<br> | ||
{{Lösung versteckt|1=Öffne das GeoGebra-Applet verändere den Wert des Schiebereglers m. Stelle m so ein, dass der Graph f,g,h,... entspricht. Die Funktionsgleichung wird dir angezeigt. | |||
<ggb_applet id="ktgybdhy" width="683" height="572" border="888888" />|2=Tipp|3=Verbergen}}</div> | |||
</div> | |||
<ggb_applet id="m6X4r2rP" width="713" height="409" border="888888" /><br> | |||
<small>Applet von Manuel Graf</small><br> | |||
{{Lösung versteckt|Öffne das GeoGebra-Applet verändere den Wert des Schiebereglers m. Stelle m so ein, dass der Graph | <br /> | ||
===Von der Funktionsgleichung zur Geraden=== | ===Von der Funktionsgleichung zur Geraden=== | ||
| Zeile 410: | Zeile 399: | ||
<br /> | <br /> | ||
{{Box|Übung 19| | {{Box|1=Übung 19|2=Zeichne die Geraden mithilfe des y-Achsenabschnittes und des Steigungsdreiecks.<br> | ||
a) f(x) = 3x + 1<br> | |||
b) f(x) = 3x - 1<br> | |||
Nutze bei Bedarf | c) f(x) = 0,5x + 2<br> | ||
}}{{Lösung versteckt|Zeichne zuerst den y-Achsenabschnitt b ein, von hier aus zeichne das Steigungsdreieck. Prüfe deine Zeichnung mit GeoGebra. | d) f(x) = <math>\tfrac{3}{4}</math>x - 3. | ||
https://www.geogebra.org/graphing|Tipp | Nutze bei Bedarf den Tipp.|3=Üben}} | ||
{{Lösung versteckt|Zeichne zuerst den y-Achsenabschnitt b ein, von hier aus zeichne das Steigungsdreieck. Prüfe deine Zeichnung mit GeoGebra. | |||
https://www.geogebra.org/graphing|Tipp |Verbergen}} | |||
{{Box|Übung 20 - Domino|Erstelle gemeinsam mit deinem Partner/deiner Partnerin ein Domino zu Linearen Funktionen.|Icon=brainy hdg-scissors}} | |||
{{Fortsetzung|vorher=2.1 Lineare Funktionen erkennen und darstellen|vorherlink=Lineare Funktionen im Aktiv-Urlaub/ | {{Fortsetzung|vorher=2.1 Lineare Funktionen erkennen und darstellen|vorherlink=Lineare Funktionen im Aktiv-Urlaub/Lineare Funktionen erkennen und darstellen|weiter=2.3) Wertetabelle und Funktionsgleichung|weiterlink=Lineare Funktionen im Aktiv-Urlaub/Wertetabelle und Funktionsgleichung}} | ||
Aktuelle Version vom 22. Mai 2022, 10:57 Uhr
0) Vorwissen zum Thema
1) Zuordnungen und Funktionen
2.1) Lineare Funktionen erkennen und darstellen
2.2) Funktionsgleichung und Funktionsgraph
2.3) Wertetabelle und Funktionsgleichung
Wertetabelle und Funktionsgraph
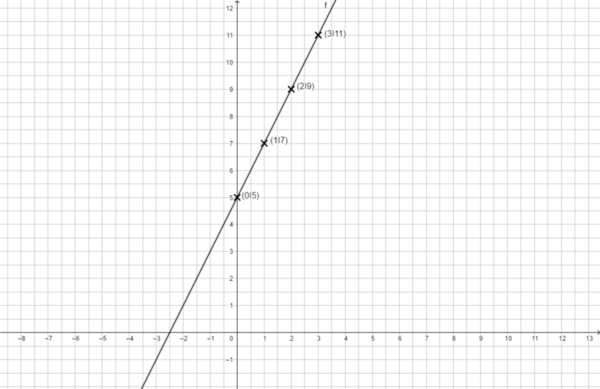
Berechne den y-Wert der Funktion, indem du den x-Wert in die Funktionsgleichung einsetzt.
Beispiel Bootsverleih: y = 2x + 5
Für x = 1 gilt: y = 2· 1 + 5
= 7
Für x = 2 gilt: y = 2· 2 + 5
= 9
Übertrage die Werte in die Wertetabelle:
| x | 0 | 1 | 2 | 3 | 4 | ... |
| y | 5 | 7 | 9 | 11 | 13 | ... |
Das Video fasst das Vorgehen noch einmal zusammen:

Applet von Hans Scharrer, jkreitner
Lege jeweils eine Wertetabelle an und zeichne den Graphen der Funktion. Zeichne a,b und c in ein Koordinatenkreuz und b, d und e in ein zweites Koordinatenkreuz. Nutze verschiedene Farben.
a) y = x
b) y = 2x
c) y = 0,5x
d) y = 2x + 1
e) y = 2x - 3
Fällt dir etwas auf?
| Aufgabe | x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| a) | y=x | |||||||
| b) | y=2x | |||||||
| c) | y=0,5x | |||||||
| d) | y=2x+1 | |||||||
| e) | y=2x-3 |
Funktionsgleichung und Funktionsgraph
f(x) = mx + b Bedeutung von m und b für den Funktionsgraphen
Damit du einen Eindruck von der Bedeutung der Parameter m (Steigung) und b (y-Achsenabschnitt) der Funktionsgleichung linearer Funktionen f(x) = mx + b erhältst, verändere in der folgenden Animation mithilfe der Schieberegler die Größe von m und b. Notiere deine Beobachtungen stichpunktartig.

In der Funktionsgleichung linearer Funktionen f(x)= m·x + b haben die Parameter m und b verschiedene Bedeutungen:
b ist der y-Achsenabschnitt, im Punkt P(0|b) schneidet die Gerade die y-Achse.
Nun schauen wir uns die Steigung m genauer an. Dazu wählen wir den y-Achsenabschnitt b = 0, die Gerade geht also durch den Ursprung (0|0).
Erinnerung: Diese Funktionen heißen "proportionale Funktionen", da ihr Graph eine Ursprungsgerade ist.
Die Steigung m
Wir unterscheiden steigende und fallende Geraden. Eine Gerade "steigt", wenn bei steigenden x-Werten auch die y-Werte steigen. Für die Steigung m gilt also:
Ist m > 0, steigt die Funktion.
Ist m < 0, fällt die Funktion.Anschaulich vorstellen kannst du dir, dass die Funktion steigt, wenn der Wanderer den Berg hochsteigen muss.
Fällt die Funktion, "fällt" der Wanderer bergab.
Um zu unterscheiden, ob eine Gerade steil oder flach verläuft (steigt oder fällt), beobachte in der nächsten Simulation den Maulwurf, der seinen Maulwurfshügel hinaufklettert.

Wenn die Steigung m steil ist, muss der Maulwurf sehr mutig sein! Fülle den nachfolgenden Lückentext aus und übertrage ihn in dein Heft:
Die Steigung m einer proportionalen (linearen) Funktion f(x) = mx bestimmt den Verlauf der Geraden:
Für m > 0 steigt die Gerade und für m < 0 fällt die Gerade.
Die Gerade steigt flach für 0< m < 1 und steil für m > 1.
Die Gerade fällt flach für -1 < m < 0 und steil für m < -1.
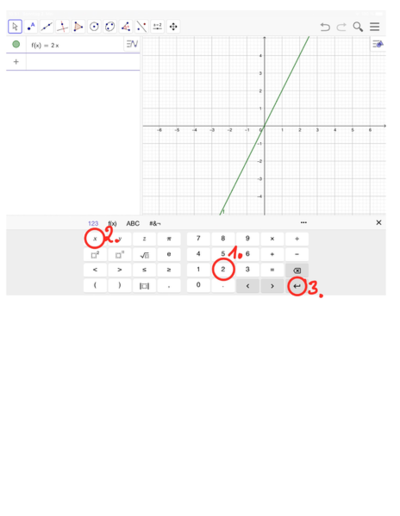
Öffne die App GeoGebra und gib die Funktionsgleichung ein. Der zugehörige Graph wird sofort angezeigt. Steigt oder fällt dieser, steil oder flach?
Teste dein Wissen mit einem Kahoot (im Unterricht).
Das Steigungsdreieck
Untersuche mithilfe der Animation in GeoGebra die Steigung von Geraden. Du kannst mit den Schiebereglern m verändern. Außerdem kannst du das Steigungsdreieck durch Verschieben der Punkte A und B verändern. Beobachte, was geschieht. Probiere aus.

Beobachtung: Die Steigung m einer linearen Funktion können wir mit einem Steigungsdreieck ermitteln und darstellen. Dazu zeichnen wir von einem beliebigen Punkt auf der Geraden ein Dreieck zu einem anderen Punkt auf der Geraden, bei dem die eine Seite parallel zur x-Achse liegt und die andere parallel zur y-Achse. Gehen wir dabei genau 1 Einheit in x-Richtung, steigt (oder fällt) der y-Wert immer um den Wert m, die Steigung.
Egal, wie das Steigungsdreieck gezeichnet wird, der Quotient aus bleibt immer gleich, dies ist die Steigung m.
Originallink zum Applet: https://www.geogebra.org/m/gjbxvqr5
Du kannst das jeweilige Steigungsdreieck einblenden lassen. Verschiebe das Steigungsdreieck durch Verschieben der angezeigten Punkte. Diskutiere deine Beobachtungen mit deinem Partner/deiner Partnerin.

Applet von Buß-Haskert
Löse auf der Seite Aufgabenfuchs die Aufgabe
- 15
Die Steigung m eines Graphen ablesen
Ist der Graph einer linearen Funktion gegeben (also eine Gerade im Koordinatensystem), kannst du die Steigung m mithilfe eines Steigungsdreiecks bestimmen.
Das nachfolgende Video erklärt, wie du bei einem gegebenen Graphen ein Steigungsdreieck einzeichnest und damit die Steigung m bestimmst.
Die Bilder zeigen dir noch einmal, wie du ein Steigungsdreieck einzeichnest und damit die Steigung m bestimmst.
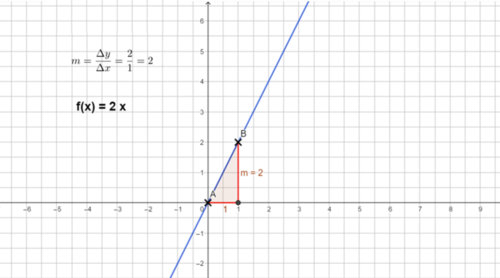
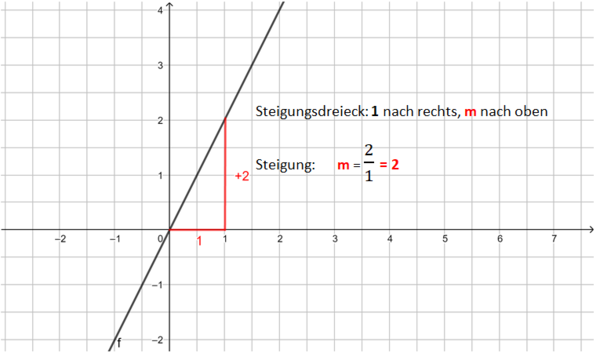
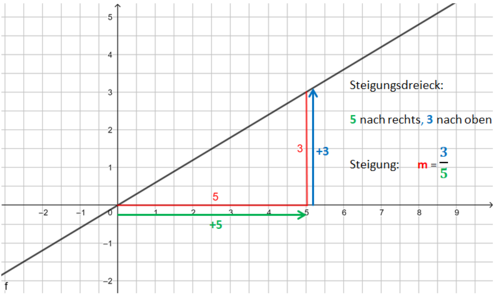
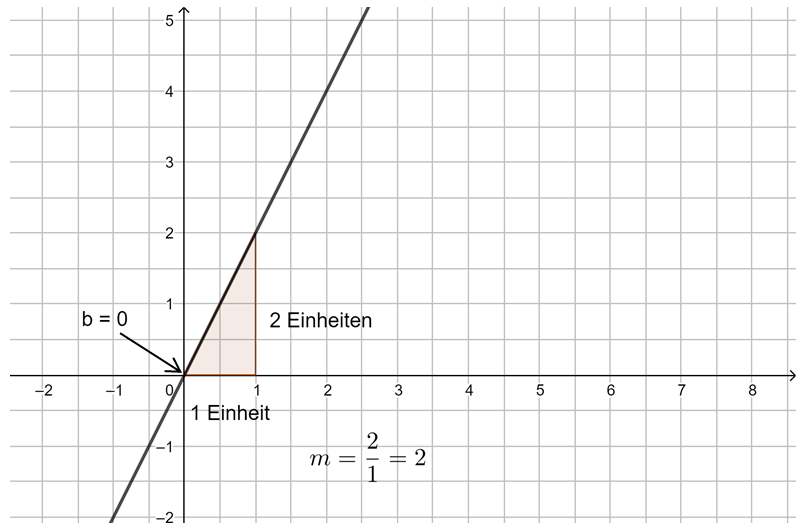
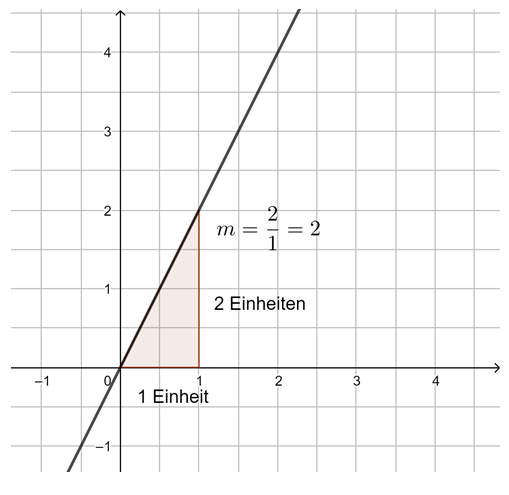
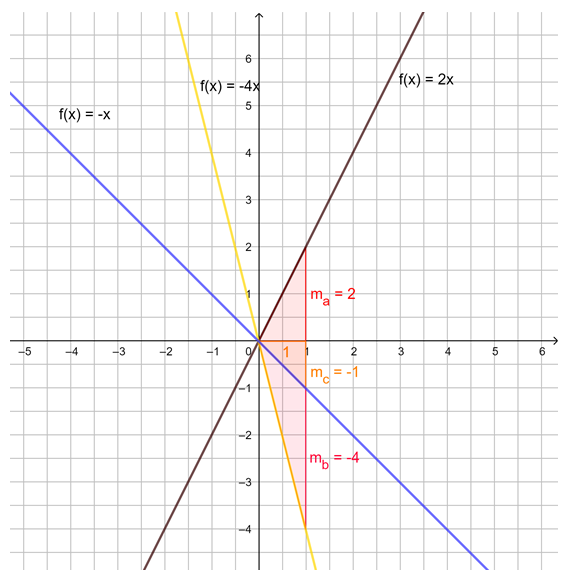
1. Beispiel: m ist eine positive ganze Zahl (also eine natürliche Zahl):
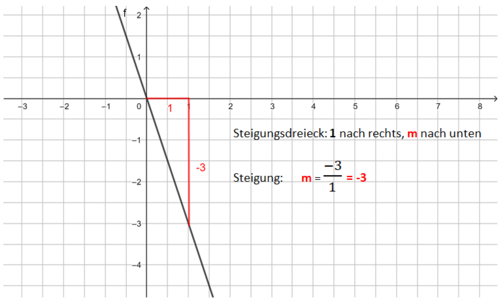
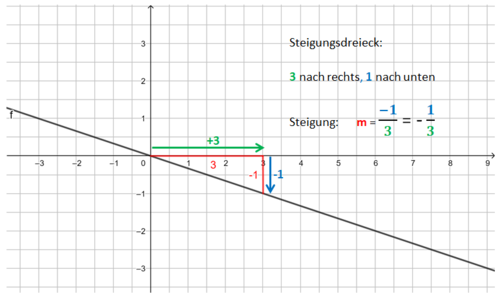
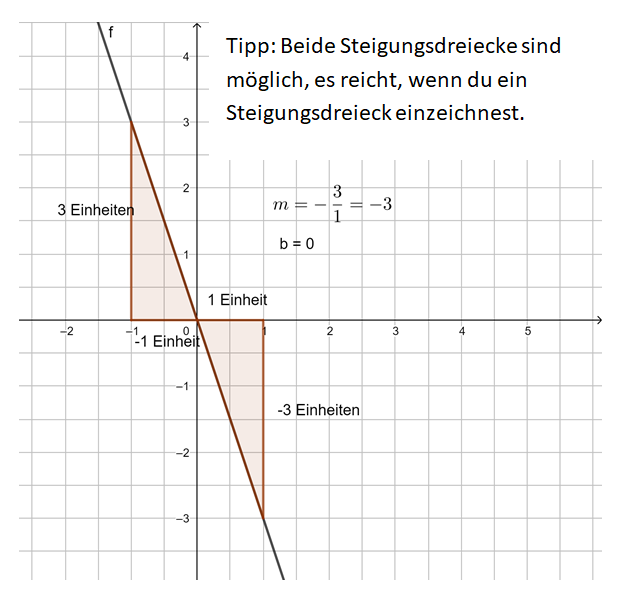
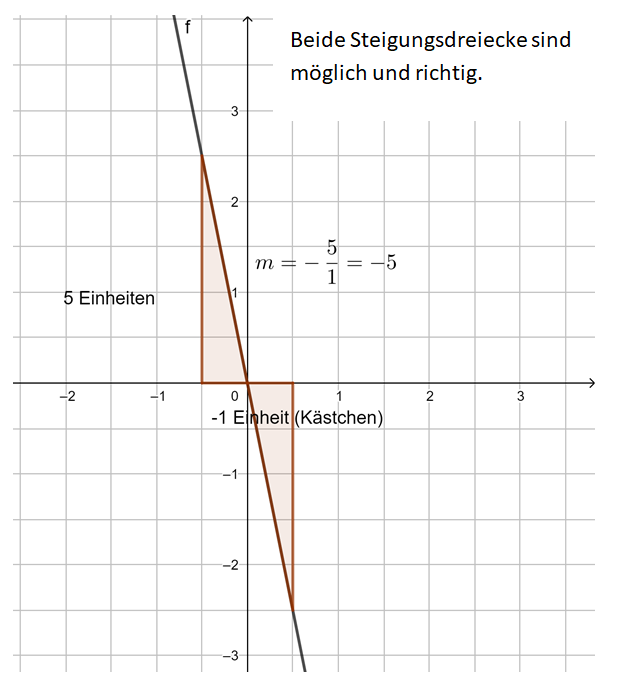
2. Beispiel: m ist eine negative ganze Zahl:
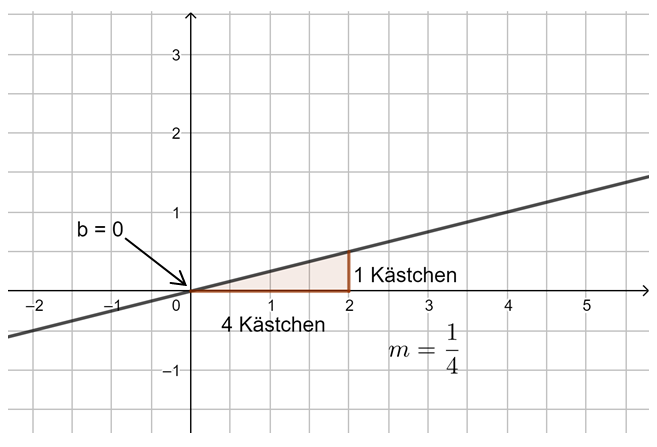
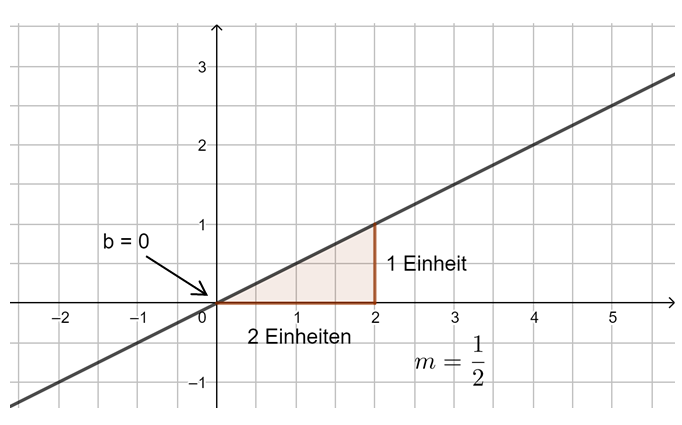
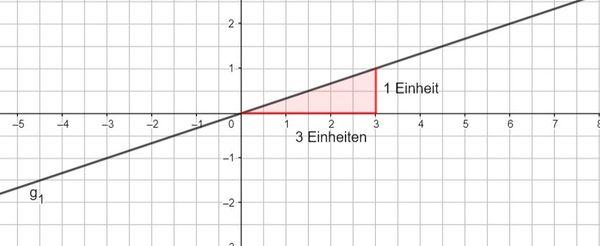
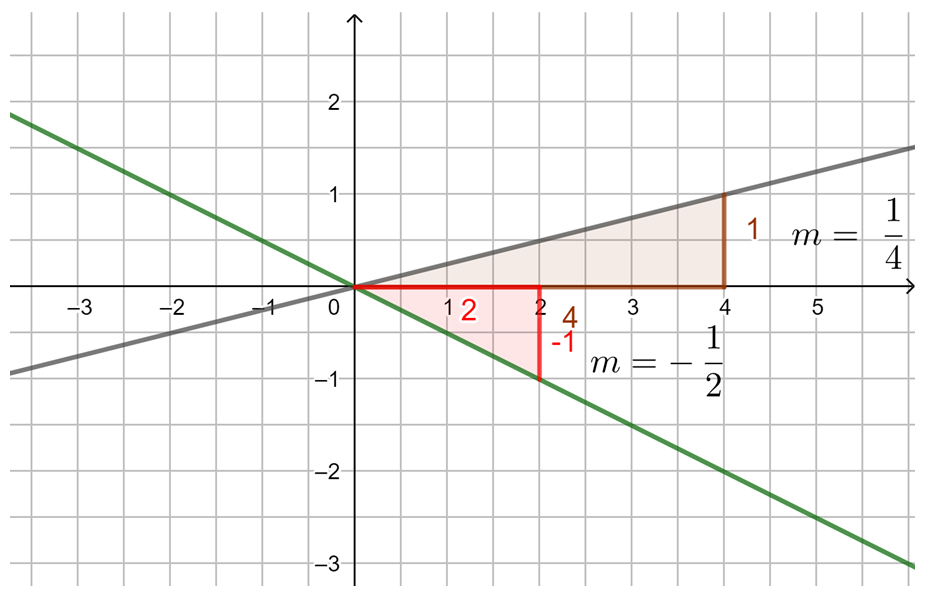
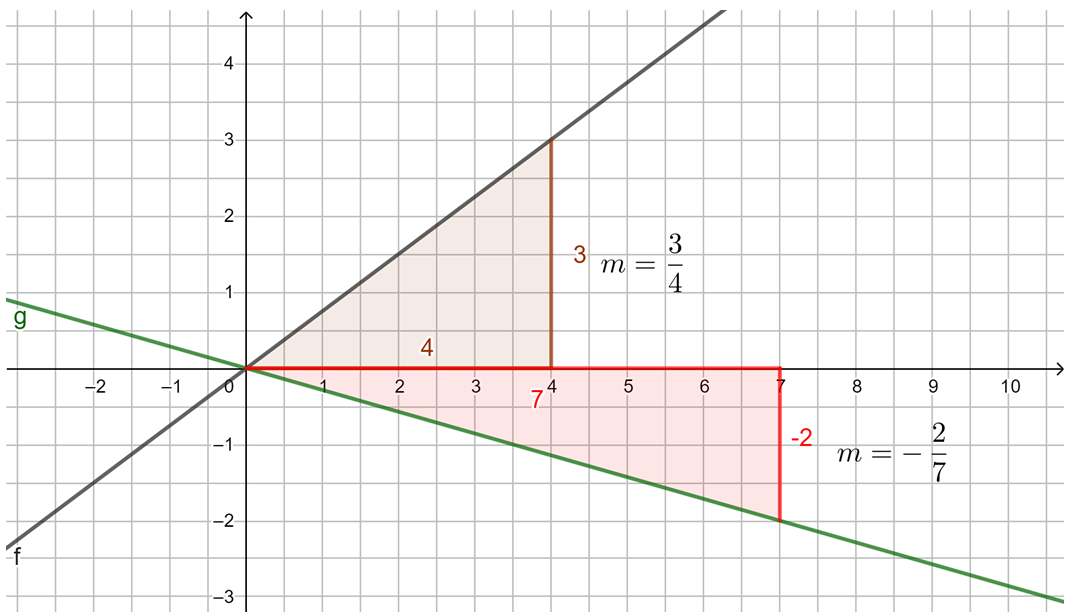
3. Beispiel: m ist ein Bruch (positiv):
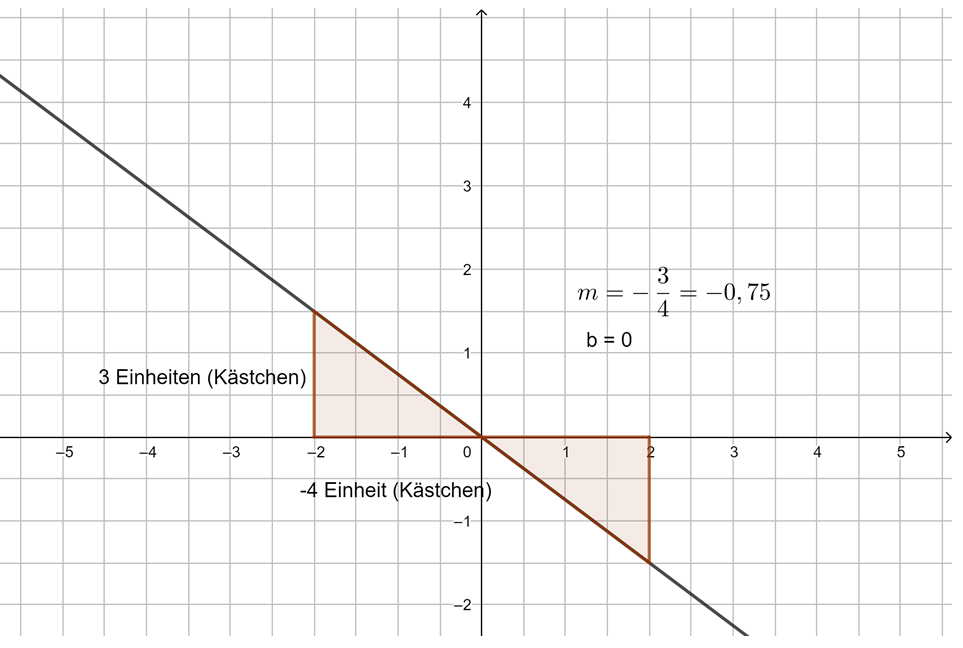
4. Beispiel: m ist ein Bruch (negativ):
Teste dein Wissen mit einem Kahoot (im Unterricht).
- 1. Thomas fährt mit seinem Fahrrad in einer Sekunde durchschnittlich 5 m.
- 2. Die Eintrittskarte für einen Kletterpark kostet pro Person 13 €.
- 3. Das Fitness-Training kostet für eine halbe Stunde 3,50 €.
- 4. Erfinde selbst ein Beispiel.
| x | 1 | 2 | 3 | ... |
| y-Strecke | 5 | 10 | ... | |
| y-Eintrittskosten | 13 | ... | ||
| y-Trainingskosten | ... |
Selbst erstellte Aufgabensammlung der Klasse 8: Proportionale Funktionen im Aktivurlaub
Erstelle eine Wertetabelle, zeichne den Graphen und gib die Funktionsgleichung an.
Aktivurlaub an der Nordsee:
1. Familie Mann fährt in den Urlaub an die Nordsee. Für 100 km benötigt ihr Auto ca. 7,8 Liter Benzin.
2. An einem Rastplatz legen sie eine Pause ein und essen eine Kleinigkeit. Ein Fischbrötchen kostet 1,50€.
3. Familie Mann möchte im Urlaub an der Nordsee surfen gehen. Für 4 Personen zahlen sie 40€ pro Stunde.
4. Nach dem Surfen gönnt sich die Familie jeweils eine Kugel Eis zu 1,10€.
5. Nachmittags gehen sie in der Nordsee schwimmen. Dabei schwimmen sie in 5 Minuten ca. 70m weit. Eine Freundin schwimmt gleichzeitig los, sie benötig für 25m 100 Sekunden. (Zeichne in ein Koordinatenkreuz)
Wanderurlaub:
6. Ein Sportgeschäft bietet Wanderstöcke an. Jeder Stock kostet 25€.
7. Familie H. unternimmt eine Wanderung. Für die Strecke von 4m benötigen sie 5 Sekunden.
Familie U. geht ebenfalls wandern. Sie schafft in 10 Minuten 500m. (Zeichne in ein Koordinatenkreuz.)
8. Für eine geführte Wanderung durch den Nationalpark zahlt die Familie 15€ pro Stunde.
9. Zum Picknick während der Wanderung gibt es Obst und Schokoriegel. Ein Riegel kostet 0,60€.
Reiterferien:
10. Familie M. macht Urlaub auf einem Reiterhof. Drei Runden Pony-Reiten um den See kosten 13,50€.
Den Graphen zeichnen mit einem Steigungsdreieck
Ist die Funktionsgleichung einer proportionalen Funktion gegeben, kannst du den Graphen (also eine Ursprungsgerade) mithilfe eines Steigungsdreiecks zeichnen.
Das nachfolgende Video erklärt, wie du bei gegebener Steigung mit dem Steigungsdreieck den Graphen (Ursprungsgerade) einer proportionalen Funktion zeichnest.
Zeichne jeweils den Graphen der proportionalen Funktion mithilfe eines Steigungsdreiecks.
a) f(x) = 2x
b) f(x) = -4x
c) f(x) = -x
d) f(x) = x
e) f(x) = -x
f) f(x) = x
Tipp zum Zeichnen von Steigungsdreiecken, wenn m ein Bruch ist (bei d bis i)
Gehe so viele Schritte, wie der NENNER angibt, nach RECHTS und
Zusammenfassung:
Schau dazu das nachfolgende Video zu Steigungsdreiecken an:
Der y-Achsenabschnitt b
Lineare Funktionen: f(x) = m·x + b
Nachdem wir uns ausführlich mit der Bedeutung von m, also der Steigung einer linearen Funktion beschäftigt haben, schau noch einmal im Applet, welche Bedeutung der Parameter b für den Graphen der Funktion hat.

Die Veränderung von b bewirkt eine Verschiebung der Geraden entlang der y-Achse.
Eine Funktion mit der Gleichung f(x) = m·x + b ist eine lineare Funktion.
Der Graph ist eine Gerade.
Diese Gerade hat die Steigung m und schneidet die y-Achse im Punkt (0|b).
Im Weiteren betrachten wir lineare Funktionen f(x) = mx + b.
Auch hier lernst du, wie du anhand eines Graphen die Funktionsgleichung bestimmst bzw. wie zu einer Funktionsgleichung eine passende Gerade zeichnen kannst.
Von der Geraden zu Funktionsgleichung
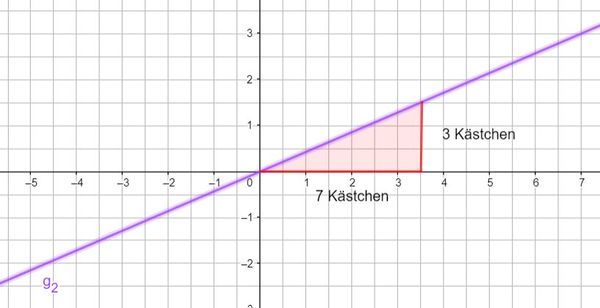
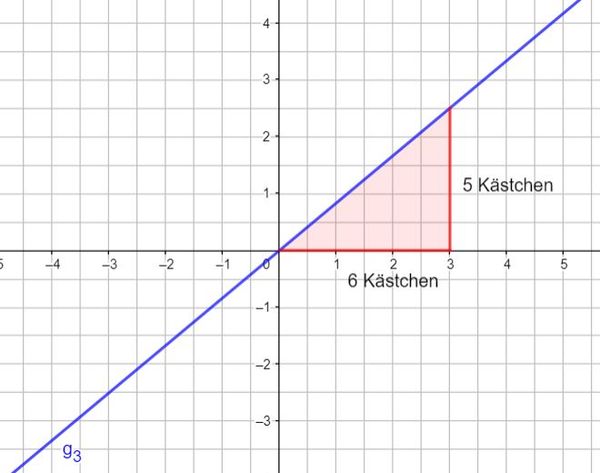
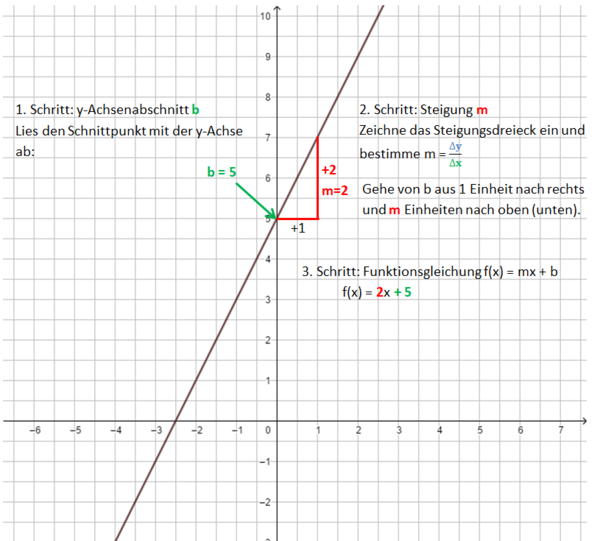
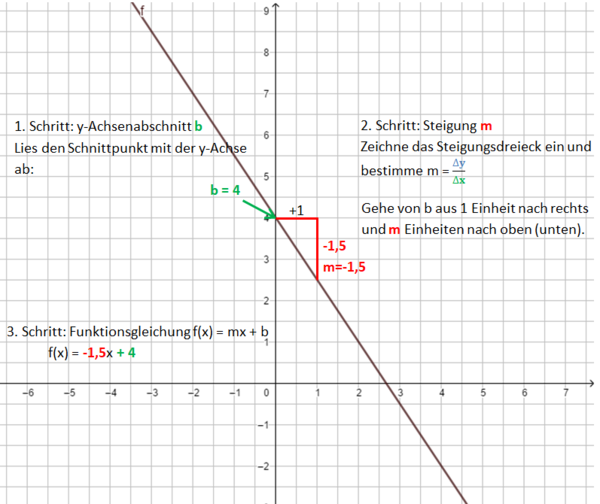
Und nun noch einmal übersichtlich als Bild: Beispiel 1 (leicht): m ist eine natürliche Zahl
Beispiel 2 (mittel): m ist eine negative ganze Zahl
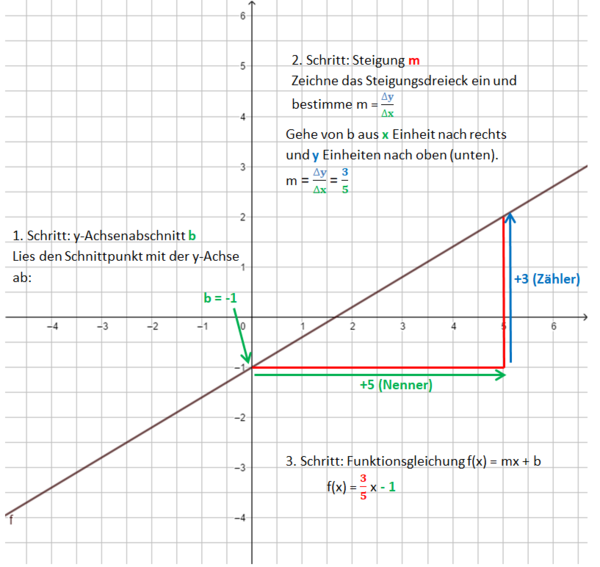
Beispiel 3 (schwer): m ist ein Bruch
Gib auf der Seite realmath jeweils die Funktionsgleichung f(x) = mx + b an. Bestimme dazu m und b, wie oben beschrieben.

Applet von Manuel Graf
Von der Funktionsgleichung zur Geraden
Dabei gehst du ähnlich vor, wie beim Bestimmen der Funktionsgleichung.
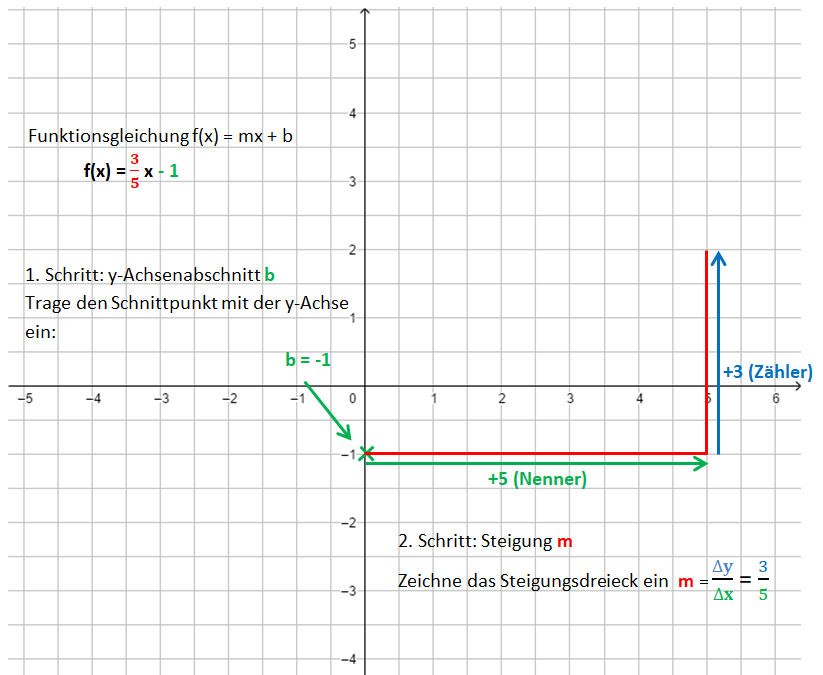
1. Schritt: Zeichne den y-Achsenabschnitt b ein: P(0|b)
2. Schritt: Zeichne das Steigungsdreieck ein. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten).
3. Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.
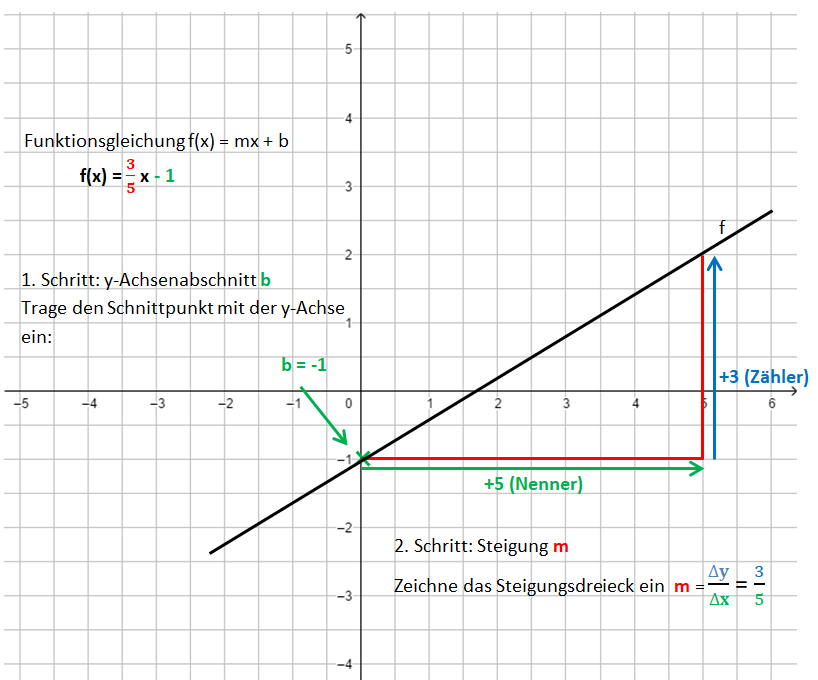
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Übertrage das Beispiel mit den Anmerkungen in dein Heft! Die Videos zeigen das Vorgehen noch einmal:

Applet von Wolfgang Wengler
Zeichne die Geraden mithilfe des y-Achsenabschnittes und des Steigungsdreiecks.
a) f(x) = 3x + 1
b) f(x) = 3x - 1
c) f(x) = 0,5x + 2
d) f(x) = x - 3.
Zeichne zuerst den y-Achsenabschnitt b ein, von hier aus zeichne das Steigungsdreieck. Prüfe deine Zeichnung mit GeoGebra.
https://www.geogebra.org/graphing