Signifikanztest für binomialverteilte Zufallsgrößen/Wiederholung Binomialverteilung: Unterschied zwischen den Versionen
K (Leerstelle vor Klammer) Markierung: Quelltext-Bearbeitung 2017 |
K (Rechtschreibfehler verbessert) Markierung: Quelltext-Bearbeitung 2017 |
||
| (58 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br>Hier wiederholst du nochmal die wichtigsten Grundlagen der Binomialverteilung.<br><br> | |||
Hier wiederholst du nochmal | In der ersten Übung wiederholst du die grundlegenden Begriffe der Binomialverteilung.<br><br> | ||
{{Box|Übung 1: | {{Box|Übung 1: wichtige Begriffe der Binomialverteilung|2= | ||
Fülle den Lückentext aus! | Fülle den Lückentext aus! | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Ein Zufallsexperiment mit genau zwei Ergebnissen (Treffer und Niete) nennt man ''' Bernoulli-Experiment'''. Wird solch ein | Ein Zufallsexperiment mit genau zwei Ergebnissen (Treffer und Niete) nennt man ''' Bernoulli-Experiment'''. Wird solch ein Experiment n-mal wiederholt und sind die Versuche unabhängig voneinander, erhält man eine '''Bernoulli-Kette''' der Länge n. Ist p die Trefferwahrscheinlichkeit und X die Zufallsvariable, welche die Anzahl k der Treffer angibt, dann kann die Wahrscheinlichkeit für k Treffer durch die '''Formel von Bernoulli''' (<math>P(X=k)=B_{n,p}(k)=\binom{n}{k}\cdot p^k\cdot(1-p)^{n-k}</math>) berechnet werden. Die Wahrscheinlichkeitsverteilung für X heißt '''Binomialverteilung''' mit den Parametern n und p. Der '''Erwartungswert''' der Binomialverteilung wird durch <math>E(X)=n\cdot p</math> berechnet. Stellt man die Binomialverteilung in einer Grafik dar (p-k Diagramm), erhält man näherungsweise eine ''' Glockenkurve'''. Der Hochpunkt der Funktion liegt beim Erwartungswert. Neben der Binomialverteilung benötigt man auch häufig die zugehörige '''Verteilungsfunktion''', für deren Wahrscheinlichkeit die Schreibweise <math>P(X\leq k)</math> üblich ist. Bei der Verteilungsfunktion werden die Wahrscheinlichkeiten bis zu einem bestimmen k-Wert aufsummiert: <math>P(X\leq k)=\sum_{i=0}^k B_{n,p}(i)</math>. | ||
</div>|3=Arbeitsmethode | </div>|3=Arbeitsmethode | ||
}} | }} | ||
<br> | |||
Vor allem die grafische Anschauung der Binomialverteilung und der Umgang mit der Verteilungsfunktion sind wichtig für die Durchführung eines Signifikanztests. Prüfe und wiederhole dein Können dazu in Übung 2. <br> | |||
{{Box|1=Übung 2: Grafische Anschauung und Berechnung von Wahrscheinlichkeiten|2= | |||
[[Datei:Kohlekraft.jpg|rechts|100px]] | |||
Die Schüler*innen der Umweltgruppe befragen 1000 Menschen in Deutschland, ob sie den Klimawandel als Bedrohung ansehen. Für die folgenden Aufgaben wird angenommen, dass immer noch 71% der Menschen in Deutschland sich durch den Klimawandel bedroht fühlen. | |||
<br><br> | |||
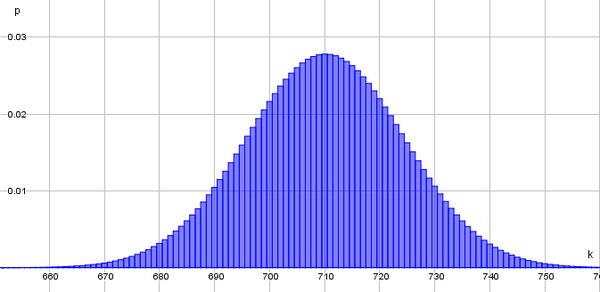
a) Skizziere die Binomialverteilung für die Befragung. | |||
{{Lösung versteckt|1= Fertige ein p-k Diagramm an. Die Binomialverteilung ist näherungsweise eine Glockenkurve. Überlege dir, wo der Hochpunkt der Funktion liegt. | |||
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | |||
{{Lösung versteckt|1= | |||
[[Datei:Neueins.png|600px]] | |||
Den Hochpunkt hat die Funktion beim Erwartungswert (<math>E(X)=n\cdot p</math>)<br> In dieser Aufgabe errechnet sich der Erwartungswert also wie folgt: <math>E(X)=1000\cdot 0.71=710</math>.<br> Hinweis! Die Breite der Glockenkurve ergibt sich aus der Standardabweichung. Für die Skizze reicht es aus, wenn du die Breite der Kurve nach Gefühl einträgst. | |||
}} | |||
Bereche die Wahrscheinlichkeit dafür,...<br><br> | |||
b) dass in der Stichprobe '''genau''' 710 Menschen den Klimawandel als Bedrohung ansehen. | |||
{{Lösung versteckt|1=In der Skizze ist die gesuchte Wahrscheinlichkeit rot markiert.<br> [[Datei:Neuzwei.png|600px]]<br>Nutze die Formel von Bernoulli!<br> Zur Berechnung nutze deinen Taschenrechner! (Hinweis: Bei den meisten Taschenrechnern ist es die Funktion binompdf(n,p,k))<br> | |||
{{Lösung versteckt|1=Nutze die Formel von Bernoulli!<br> | |||
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | |2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math> | <math>B_{1000,0.71}(710)=\binom{1000}{710}\cdot 0.71^{710}\cdot (1-0.71)^{290}=0.0278</math><br> | ||
Die Wahrscheinlichkeit, dass in der Stichprobe genau 710 Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,78 %. | |||
}} | }} | ||
c) dass '''höchstens''' 680 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen. | |||
{{Lösung versteckt|1=Nutze die | {{Lösung versteckt|1= Höchtens heißt, es können 0,1,2,3, ...,680 der Befragten den Klimawandel als Bedrohung ansehen.<br>In der Skizze ist die gesuchte Wahrscheinlichkeit rot markiert.<br>[[Datei:NeuDrei.png|600px]]<br> | ||
Nutze die Verteilungsfunktion (siehe Übung 1).<br> Zur Berechnung nutze deinen Taschenrechner! (Hinweis: Bei den meisten Taschenrechnern ist es die Funktion binomcdf(n,p,k))<br> | |||
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | |2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math>P(X\leq680)=\sum_{i=0}^{680} B_{1000,0,71} (i) = 0,0206</math> | <math>P(X\leq680)=\sum_{i=0}^{680} B_{1000,0,71} (i) = 0,0206</math><br> | ||
Die Wahrscheinlichkeit, dass in der Stichprobe höchstens 680 der Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,06 % | Die Wahrscheinlichkeit, dass in der Stichprobe höchstens 680 der Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,06. % | ||
}} | }} | ||
d) dass '''mindestens''' 740 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen. | |||
{{Lösung versteckt|1= P( | {{Lösung versteckt|1= Mindestens heißt, es können 740, 741, ...,1000 der Befragten den Klimawandel als Bedrohung ansehen.<br> In der Skizze ist die gesuchte Wahrscheinlichkeit rot markiert. <br> [[Datei:NeuVier.png|600px]] | ||
Mindestwahrscheinlichkeiten werden über die Gegenwahrscheinlichkeit berechnet:<br> <math>P(X\geq k)= 1-P(X\leq k-1)</math><br> Die Wahrscheinlichkeit für höchstens kannst du wieder mit dem Taschenrechner berechnen. Hinweis! Merke dir diesen Trick! Du brauchst ihn später noch beim Signifikanztest.<br> | |||
|2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | |2=gestufte Hilfe einblenden|3= gestufte Hilfe ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<math>P(X\geq740)=1-P(X\leq739)=0,0191</math><br> Die Wahrscheinlichkeit, dass in der Stichprobe mindestens 740 Menschen den Klimawandel als Bedrohung ansehen, beträgt 1,91 %. | <math>P(X\geq740)=1-P(X\leq739)=0,0191</math><br> | ||
Die Wahrscheinlichkeit, dass in der Stichprobe mindestens 740 Menschen den Klimawandel als Bedrohung ansehen, beträgt 1,91 %. | |||
}} | }} | ||
| Zeile 40: | Zeile 54: | ||
'''Super gemacht! Dann geht es jetzt weiter mit dem Signifikanztest! ''' | '''Super gemacht! Dann geht es jetzt weiter mit dem Signifikanztest! ''' | ||
{{Fortsetzung|weiter= | {{Fortsetzung|weiter=Grundidee vom Signifikanztest|weiterlink=Signifikanztest für binomialverteilte Zufallsgrößen/Grundidee_vom_Signifikanztest}} | ||
Aktuelle Version vom 6. März 2020, 20:48 Uhr
Hier wiederholst du nochmal die wichtigsten Grundlagen der Binomialverteilung.
In der ersten Übung wiederholst du die grundlegenden Begriffe der Binomialverteilung.
Fülle den Lückentext aus!
Ein Zufallsexperiment mit genau zwei Ergebnissen (Treffer und Niete) nennt man Bernoulli-Experiment. Wird solch ein Experiment n-mal wiederholt und sind die Versuche unabhängig voneinander, erhält man eine Bernoulli-Kette der Länge n. Ist p die Trefferwahrscheinlichkeit und X die Zufallsvariable, welche die Anzahl k der Treffer angibt, dann kann die Wahrscheinlichkeit für k Treffer durch die Formel von Bernoulli () berechnet werden. Die Wahrscheinlichkeitsverteilung für X heißt Binomialverteilung mit den Parametern n und p. Der Erwartungswert der Binomialverteilung wird durch berechnet. Stellt man die Binomialverteilung in einer Grafik dar (p-k Diagramm), erhält man näherungsweise eine Glockenkurve. Der Hochpunkt der Funktion liegt beim Erwartungswert. Neben der Binomialverteilung benötigt man auch häufig die zugehörige Verteilungsfunktion, für deren Wahrscheinlichkeit die Schreibweise üblich ist. Bei der Verteilungsfunktion werden die Wahrscheinlichkeiten bis zu einem bestimmen k-Wert aufsummiert: .
Vor allem die grafische Anschauung der Binomialverteilung und der Umgang mit der Verteilungsfunktion sind wichtig für die Durchführung eines Signifikanztests. Prüfe und wiederhole dein Können dazu in Übung 2.
Die Schüler*innen der Umweltgruppe befragen 1000 Menschen in Deutschland, ob sie den Klimawandel als Bedrohung ansehen. Für die folgenden Aufgaben wird angenommen, dass immer noch 71% der Menschen in Deutschland sich durch den Klimawandel bedroht fühlen.
a) Skizziere die Binomialverteilung für die Befragung.
In dieser Aufgabe errechnet sich der Erwartungswert also wie folgt: .
Hinweis! Die Breite der Glockenkurve ergibt sich aus der Standardabweichung. Für die Skizze reicht es aus, wenn du die Breite der Kurve nach Gefühl einträgst.
Bereche die Wahrscheinlichkeit dafür,...
b) dass in der Stichprobe genau 710 Menschen den Klimawandel als Bedrohung ansehen.
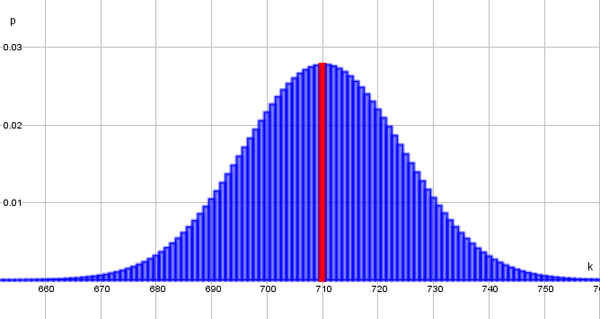
Nutze die Formel von Bernoulli!
Zur Berechnung nutze deinen Taschenrechner! (Hinweis: Bei den meisten Taschenrechnern ist es die Funktion binompdf(n,p,k))
c) dass höchstens 680 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen.
Höchtens heißt, es können 0,1,2,3, ...,680 der Befragten den Klimawandel als Bedrohung ansehen.
In der Skizze ist die gesuchte Wahrscheinlichkeit rot markiert.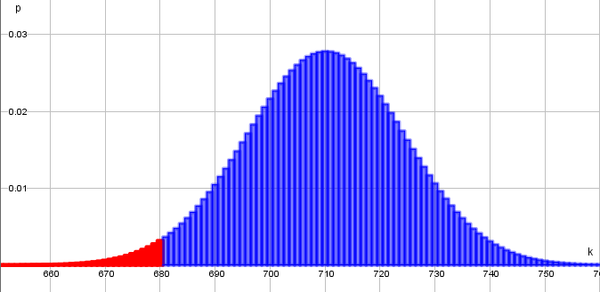
Zur Berechnung nutze deinen Taschenrechner! (Hinweis: Bei den meisten Taschenrechnern ist es die Funktion binomcdf(n,p,k))
d) dass mindestens 740 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen.
Mindestens heißt, es können 740, 741, ...,1000 der Befragten den Klimawandel als Bedrohung ansehen.
In der Skizze ist die gesuchte Wahrscheinlichkeit rot markiert.
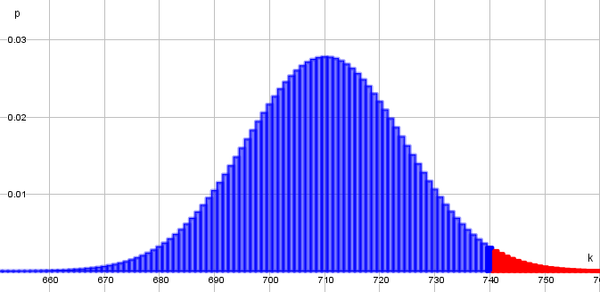
Die Wahrscheinlichkeit für höchstens kannst du wieder mit dem Taschenrechner berechnen. Hinweis! Merke dir diesen Trick! Du brauchst ihn später noch beim Signifikanztest.
Super gemacht! Dann geht es jetzt weiter mit dem Signifikanztest!