Quadratische Funktionen erforschen/Die Parameter der Normalform: Unterschied zwischen den Versionen
K (15 Versionen importiert) |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
{{Quadratische Funktionen erforschen}} | {{Navigation verstecken|{{Quadratische Funktionen erforschen}}}} | ||
{{Box | |||
| | |||
|In diesem Kapitel stellen sich die Parameter der Normalform quadratischer Funktionen vor. Du kannst herausfinden, | |||
#wie man Parabeln strecken, stauchen und spiegeln kann, | |||
#welchen Einfluss die Parameter der Normalform auf das Aussehen und die Lage der Parabel haben und | |||
#wie du das an den Funktionstermen erkennen kannst. | |||
|Kurzinfo | |||
}} | |||
==Strecken, Stauchen und Spiegeln== | |||
== | |||
{{Box | |||
|Achtung | |||
|Dieser Abschnitt ist identisch zu dem 1. Abschnitt in dem Kapitel [[{{BASEPAGENAME}}/Die Parameter der Scheitelpunktform|die Parameter der Scheitelpunktform]]. Wenn du ihn dort schon bearbeitet hast, kannst du direkt weitergehen zum nächsten Abschnitt '''"Der Parameter b"'''. | |||
|Hervorhebung1 | |||
}} | |||
{{Box | |||
|Aufgabe 1 | |||
|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 4). | |||
[[Datei:Notepad-117597.svg|40px|right|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
Was passiert, wenn man statt der Funktion <math>y=x^2</math> folgende Funktionen gegeben hat: | Was passiert, wenn man statt der Funktion <math>y=x^2</math> folgende Funktionen gegeben hat: | ||
::(1) <math>y= | ::(1) <math>y=2x^2</math>, (2) <math>y=\frac{1}{2}x^2</math> und (3) <math>y=-x^2</math> ? | ||
'''a)''' Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen (ohne diese zu zeichnen!). | '''a)''' Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen (ohne diese zu zeichnen!). | ||
{{Lösung versteckt|1=Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die drei Funktionen aufstellen und die Funktionswerte mit den Werten von <math>y=x^2</math> vergleichen.|2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
'''b)''' Zeichne die drei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren? | |||
|Arbeitsmethode | |||
}} | |||
In dem Applet ist die Normalparabel <math>f(x)=x^2</math>, die du auf der Seite [[{{BASEPAGENAME}}/Quadratische Funktionen kennenlernen|Quadratische Funktionen kennenlernen]] erkundet hast, eingezeichnet. Du kannst den Schieberegler a betätigen und dadurch den Graph <math>g(x)</math> verändern. Was passiert? | |||
<ggb_applet width="100%" height="500" version="4.2" showMenuBar="true" showResetIcon="true" id="eK5MmMmb" /> | |||
{{Box | |||
|Aufgabe 2 | |||
|In dem folgenden Lückentext werden die Erkenntnisse, die du aus Aufgabe 1 mitnehmen konntest, noch einmal ausformuliert. Füge die fehlenden Begriffe und Zahlen in die Lücken. | |||
{{LearningApp|app=pm1vv0zbj16|height=375px}} | |||
|Arbeitsmethode | |||
}} | |||
{{Box | |||
|Aufgabe 3 | |||
|'''Knobelaufgabe''' | |||
{{LearningApp|app=pcssvbrfj16|height=500px}} | |||
|Arbeitsmethode | |||
}} | |||
==Der Parameter b== | |||
{{ | {{Box | ||
|Aufgabe 4 | |||
|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 10) [[Datei:Notepad-117597.svg|40px|right|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
| Zeile 93: | Zeile 76: | ||
'''a)''' Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!). | '''a)''' Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!). | ||
{{Lösung versteckt|1=Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die Funktionen aufstellen und die Funktionswerte mit den Werten von <math>y=x^2</math> vergleichen.|3=Hilfe verbergen}} | |||
'''b)''' Zeichne die zwei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren? | |||
|Arbeitsmethode | |||
}} | |||
In dem Applet ist die Normalparabel <math>f(x)=x^2</math>, die du auf der Seite [[{{BASEPAGENAME}}/Quadratische Funktionen kennenlernen|Quadratische Funktionen kennenlernen]] erkundet hast, eingezeichnet. Du kannst den Schieberegler b betätigen und dadurch den Graph <math>g(x)</math> verändern. Was passiert? | |||
<ggb_applet width="100%" height="571" version="4.2" showMenuBar="true" showResetIcon="true" id="MyuG9D2b" /> | |||
{{ | {{Box | ||
|Aufgabe 5 | |||
|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 11) und einen Partner''' [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]] [[Datei:Puzzle-1020221 640.jpg|125px|rahmenlos|Partnerarbeit]]. | |||
'''a)''' | '''a)''' | ||
{{LearningApp|app=pyf382e7a17|width=70%|height=500px}} | |||
{{Lösung versteckt|1=Wie sieht der Graph aus: Ist er nach oben oder nach unten geöffnet? Nach rechts oder nach links verschoben? | |||
Wende dein Wissen über die Parameter a und b an.|2= Hilfe anzeigen|3=Hilfe verstecken}} | |||
'''b)''' Überlege dir einen Tipp für deinen Partner, wie er die passenden Terme beim Pferderennen herausfinden kann. Notiere den Tipp in deinem Hefter. | '''b)''' Überlege dir einen Tipp für deinen Partner, wie er die passenden Terme beim Pferderennen herausfinden kann. Notiere den Tipp in deinem Hefter. | ||
'''c)''' Vergleiche deinen Tipp mit dem deines Partners an dich. | '''c)''' Vergleiche deinen Tipp mit dem deines Partners an dich. | ||
{{Lösung versteckt|1=[[Datei:Beispiel-Tipp Pferderennen.PNG|rahmenlos|600px|Parameter b]]|2=Beispiel Tipp anzeigen|3=Beispiel Tipp verbergen}} | |||
|Arbeitsmethode | |||
}} | }} | ||
{{Box | |||
{{ | |Merke | ||
|Addiert man den Ausdruck <math>bx</math> zu <math>y=ax^2</math>, wird die Parabel sowohl in x- als auch in y-Richtung verschoben. Für <math>y=ax^2+bx</math> gilt: | |||
<u>Für '''a>0:'''</u> | <u>Für '''a>0:'''</u> | ||
| Zeile 135: | Zeile 120: | ||
'''b>0''': Die Parabel wird nach rechts und oben verschoben. | '''b>0''': Die Parabel wird nach rechts und oben verschoben. | ||
'''b<0''': Die Parabel wird nach links und oben verschoben.}} | '''b<0''': Die Parabel wird nach links und oben verschoben. | ||
|Merksatz | |||
}} | |||
==Der Parameter c== | |||
{{Box | |||
{{ | |Aufgabe 6 | ||
|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 11) [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | |||
| Zeile 148: | Zeile 137: | ||
'''a)''' Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!). | '''a)''' Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!). | ||
{{Lösung versteckt|1=Wenn du dir unsicher bei der Formulierung deiner Vermutungen bist, kannst du Wertetabellen für die Funktionen aufstellen und die Funktionswerte mit den Werten von <math>y=x^2</math> vergleichen.|2= Hilfe anzeigen|3=Hilfe verstecken}} | |||
'''b)''' Zeichne die zwei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren? | |||
|Arbeitsmethode | |||
}} | |||
In dem Applet ist die Normalparabel <math>f(x)=x^2</math>, die du auf der Seite [[{{BASEPAGENAME}}/Quadratische Funktionen kennenlernen|Quadratische Funktionen kennenlernen]] erkundet hast, eingezeichnet. Du kannst die Schieberegler a, b und c betätigen und dadurch den Graph <math>g(x)</math> verändern. Was passiert? | |||
<ggb_applet width="100%" height="571" version="4.2" showMenuBar="true" showResetIcon="true" id="uV5keF5j" /> | |||
{{Box | |||
{{ | |Aufgabe 7 | ||
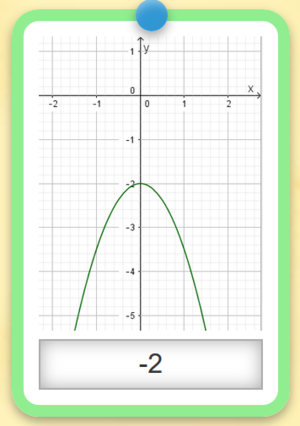
'''Welchen Wert hat der Parameter c?''' Trage deine Lösung wie in dem '''Beispiel''' ein: | |'''Welchen Wert hat der Parameter c?''' Trage deine Lösung wie in dem '''Beispiel''' ein: | ||
::[[Datei:Beispiel Parameter c.PNG|rahmenlos|Beispiel]] | ::[[Datei:Beispiel Parameter c.PNG|rahmenlos|Beispiel]] | ||
{{LearningApp|app=p8zh59fa317|width=100%|height=700px}} | |||
|Arbeitsmethode | |||
}} | }} | ||
<div class="mw-collapsible mw-collapsed" data-expandtext="Hilfe" data-collapsetext="Hilfe verbergen"> | |||
Der Paramter c gibt den y-Achsenabschnitt an. Du kannst ihn an dem Punkt P(0|c) ablesen.</div> | |||
{{Box | |||
{{Merke | |Merke | ||
|Der Parameter c bewirkt eine Verschiebung der Parabel in y-Richtung. Er gibt dabei den '''y-Achsenabschnitt''' der Parabel <math>y=ax^2+bx+c</math> an. Es gilt für: | |||
'''c>0''': Die Parabel wird nach oben verschoben. | '''c>0''': Die Parabel wird nach oben verschoben. | ||
'''c<0''': Die Parabel wird nach unten verschoben.}} | '''c<0''': Die Parabel wird nach unten verschoben. | ||
|Merksatz | |||
}} | |||
== | ==Zusammenfassung der wichtigsten Inhalte== | ||
{{Box | |||
|Aufgabe 8 | |||
| | |'''Für diese Aufgabe benötigst du deinen Hefter (Merkliste, S. 4) [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | ||
|} | Ergänze die folgenden Merksätze durch Beispiele. | ||
|Arbeitsmethode | |||
}} | |||
{{Merke | {{Box | ||
|Merke | |||
| | |||
Multipliziert man <math>y=x^2</math> mit einem Faktor a, wird die Parabel '''gestreckt, gestaucht''' und/oder '''gespiegelt'''. <math>y=ax^2</math> (mit a≠0) ergibt demnach für: | Multipliziert man <math>y=x^2</math> mit einem Faktor a, wird die Parabel '''gestreckt, gestaucht''' und/oder '''gespiegelt'''. <math>y=ax^2</math> (mit a≠0) ergibt demnach für: | ||
| Zeile 209: | Zeile 200: | ||
'''-1 < a < 1''': Die Parabel ist gestaucht. | '''-1 < a < 1''': Die Parabel ist gestaucht. | ||
Der Parameter a wird auch '''Streckungsfaktor''' genannt.}} | Der Parameter a wird auch '''Streckungsfaktor''' genannt. | ||
|Merksatz | |||
}} | |||
{{Merke | {{Box | ||
|Merke | |||
|Addiert man den Ausdruck <math>bx</math> zu <math>y=ax^2</math>, wird die Parabel sowohl in x- als auch in y-Richtung verschoben. Für <math>y=ax^2+bx</math> gilt: | |||
<u>Für '''a>0:'''</u> | <u>Für '''a>0:'''</u> | ||
| Zeile 224: | Zeile 219: | ||
'''b>0''': Die Parabel wird nach rechts und oben verschoben. | '''b>0''': Die Parabel wird nach rechts und oben verschoben. | ||
'''b<0''': Die Parabel wird nach links und oben verschoben.}} | '''b<0''': Die Parabel wird nach links und oben verschoben. | ||
|Merksatz | |||
}} | |||
{{Merke | {{Box | ||
|Merke | |||
|Der Parameter c bewirkt eine Verschiebung der Parabel in y-Richtung. Er gibt dabei den '''y-Achsenabschnitt''' der Parabel <math>y=ax^2+bx+c</math> an. Es gilt für: | |||
'''c>0''': Die Parabel wird nach oben verschoben. | '''c>0''': Die Parabel wird nach oben verschoben. | ||
'''c<0''': Die Parabel wird nach unten verschoben.}} | '''c<0''': Die Parabel wird nach unten verschoben. | ||
|Merksatz | |||
}} | |||
[[Datei:Binoculars-1026426 640.jpg|rahmenlos|links|Ausblick|100px]] | [[Datei:Binoculars-1026426 640.jpg|rahmenlos|links|Ausblick|100px]] | ||
Die auf dieser Seite gewonnen '''Erkenntnisse können kombiniert werden''' und ergeben quadratische | Die auf dieser Seite gewonnen '''Erkenntnisse können kombiniert werden''' und ergeben quadratische Funktion der Form <math>y=ax^2+bx+c</math>. Diese Form heißt '''Normalform'''. | ||
Auf der [[ | Auf der [[{{BASEPAGENAME}}/Die Normalform|nächsten Seite]] lernst du diese Variante quadratischer Funktionen genauer kennen. Außerdem befinden sich noch weitere Übungsaufgaben in dem Kapitel [[{{BASEPAGENAME}}/Übungen|Übungen]]. | ||
{{Fortsetzung|weiter=Die Normalform|weiterlink=Quadratische Funktionen erforschen/Die Normalform}} | |||
Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]]) | Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]]) | ||
[[Kategorie:Mathematik]] | |||
[[Kategorie:ZUM2Edutags]] | |||
[[Kategorie:Quadratische Funktion]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:Learning-App]] | |||
[[Kategorie:Geogebra]] | |||
Version vom 12. November 2018, 19:13 Uhr
In diesem Kapitel stellen sich die Parameter der Normalform quadratischer Funktionen vor. Du kannst herausfinden,
- wie man Parabeln strecken, stauchen und spiegeln kann,
- welchen Einfluss die Parameter der Normalform auf das Aussehen und die Lage der Parabel haben und
- wie du das an den Funktionstermen erkennen kannst.
Strecken, Stauchen und Spiegeln
Dieser Abschnitt ist identisch zu dem 1. Abschnitt in dem Kapitel die Parameter der Scheitelpunktform. Wenn du ihn dort schon bearbeitet hast, kannst du direkt weitergehen zum nächsten Abschnitt "Der Parameter b".
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 4).
.Was passiert, wenn man statt der Funktion folgende Funktionen gegeben hat:
- (1) , (2) und (3) ?
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen (ohne diese zu zeichnen!).
b) Zeichne die drei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?
In dem Applet ist die Normalparabel , die du auf der Seite Quadratische Funktionen kennenlernen erkundet hast, eingezeichnet. Du kannst den Schieberegler a betätigen und dadurch den Graph verändern. Was passiert?

In dem folgenden Lückentext werden die Erkenntnisse, die du aus Aufgabe 1 mitnehmen konntest, noch einmal ausformuliert. Füge die fehlenden Begriffe und Zahlen in die Lücken.
Knobelaufgabe
Der Parameter b
Was passiert, wenn man statt der Funktion folgende Funktionen gegeben hat:
- (1) , (2) ?
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!).
b) Zeichne die zwei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?
In dem Applet ist die Normalparabel , die du auf der Seite Quadratische Funktionen kennenlernen erkundet hast, eingezeichnet. Du kannst den Schieberegler b betätigen und dadurch den Graph verändern. Was passiert?

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 11) und einen Partner ![]()
 .
.
a)
Wie sieht der Graph aus: Ist er nach oben oder nach unten geöffnet? Nach rechts oder nach links verschoben?
Wende dein Wissen über die Parameter a und b an.b) Überlege dir einen Tipp für deinen Partner, wie er die passenden Terme beim Pferderennen herausfinden kann. Notiere den Tipp in deinem Hefter.
c) Vergleiche deinen Tipp mit dem deines Partners an dich.
Addiert man den Ausdruck zu , wird die Parabel sowohl in x- als auch in y-Richtung verschoben. Für gilt:
Für a>0:
b>0: Die Parabel wird nach links und unten verschoben.
b<0: Die Parabel wird nach rechts und unten verschoben.
Für a<0:
b>0: Die Parabel wird nach rechts und oben verschoben.
b<0: Die Parabel wird nach links und oben verschoben.
Der Parameter c
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 11) ![]() .
.
Was passiert, wenn man statt der Funktion folgende Funktionen gegeben hat:
- (1) , (2) ?
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen (ohne diese zu zeichnen!).
b) Zeichne die zwei Graphen in ein Koordinatensystem und überprüfe deine Vermutungen aus Aufgabenteil a). Welche deiner Vermutungen treffen zu? Welche kannst du mit Hilfe der Funktionsgraphen korrigieren?
In dem Applet ist die Normalparabel , die du auf der Seite Quadratische Funktionen kennenlernen erkundet hast, eingezeichnet. Du kannst die Schieberegler a, b und c betätigen und dadurch den Graph verändern. Was passiert?

Der Parameter c bewirkt eine Verschiebung der Parabel in y-Richtung. Er gibt dabei den y-Achsenabschnitt der Parabel an. Es gilt für:
c>0: Die Parabel wird nach oben verschoben.
c<0: Die Parabel wird nach unten verschoben.
Zusammenfassung der wichtigsten Inhalte
Multipliziert man mit einem Faktor a, wird die Parabel gestreckt, gestaucht und/oder gespiegelt. (mit a≠0) ergibt demnach für:
a > 0: Die Parabel ist nach oben geöffnet.
a < 0: Die Parabel ist nach unten geöffnet.
a < -1 bzw. a > 1: Die Parabel ist gestreckt.
-1 < a < 1: Die Parabel ist gestaucht.
Der Parameter a wird auch Streckungsfaktor genannt.
Addiert man den Ausdruck zu , wird die Parabel sowohl in x- als auch in y-Richtung verschoben. Für gilt:
Für a>0:
b>0: Die Parabel wird nach links und unten verschoben.
b<0: Die Parabel wird nach rechts und unten verschoben.
Für a<0:
b>0: Die Parabel wird nach rechts und oben verschoben.
b<0: Die Parabel wird nach links und oben verschoben.
Der Parameter c bewirkt eine Verschiebung der Parabel in y-Richtung. Er gibt dabei den y-Achsenabschnitt der Parabel an. Es gilt für:
c>0: Die Parabel wird nach oben verschoben.
c<0: Die Parabel wird nach unten verschoben.
Die auf dieser Seite gewonnen Erkenntnisse können kombiniert werden und ergeben quadratische Funktion der Form . Diese Form heißt Normalform.
Auf der nächsten Seite lernst du diese Variante quadratischer Funktionen genauer kennen. Außerdem befinden sich noch weitere Übungsaufgaben in dem Kapitel Übungen.
Erstellt von: Elena Jedtke (Diskussion)