Potenzfunktionen - Einführung: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Petra Bader
Keine Bearbeitungszusammenfassung
K (Textersetzung - „\{\{Weiter\|([^|]+?)\|([^|]+?)\}\}“ durch „{{Fortsetzung|weiter=$2|weiterlink=$1}}“)
 
(25 dazwischenliegende Versionen von 9 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
{{Navigation verstecken|{{Lernpfad Potenzfunktionen}}|Lernschritte einblenden|Lernschritte ausblenden}}
'''[[Potenzfunktionen|Start]] - [[Potenzfunktionen_Einführung|Einführung]] - [[Potenzfunktionen_1. Stufe|1. Stufe]] - [[Potenzfunktionen_2. Stufe|2. Stufe]] - [[Potenzfunktionen_3. Stufe|3. Stufe]] - [[Potenzfunktionen_4. Stufe|4. Stufe]] - [[Potenzfunktionen_5. Stufe|5. Stufe]]'''</div>
__NOTOC__
== Einführung==
== Die Graphen der Funktionen x, x² und x³==


{{Box|1=Aufgabe|2=
<div class="grid">
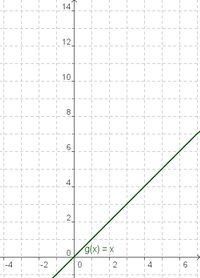
<div class="width-1-3">[[Bild:graphx.jpg|200px]]</div>
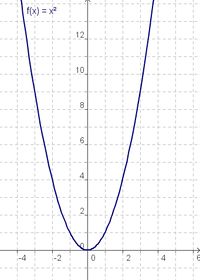
<div class="width-1-3">[[Bild:xhoch2.jpg|200px]]</div>
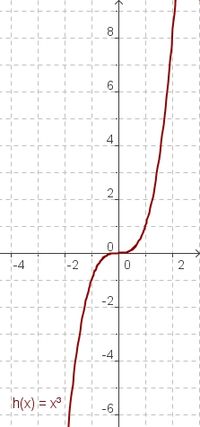
<div class="width-1-3">[[Bild:graphxhoch3.jpg|200px]] </div>
</div>


== Einführung==
# Vergleiche den Graph der Funktion h(x) = x<sup>3</sup> mit dem Graphen der Funktion g(x) = x. Beschreibe Gemeinsamkeiten und Unterschiede!
== Die Graphen der Funktionen x, x² und x³==
{| class="prettytable" cellspacing="10"
|-
| [[Bild:graphx.jpg |250px]] || [[Bild:xhoch2.jpg |250px]] ||[[Bild:graphxhoch3.jpg | 200px]]
|-
| '''g(x) = x''' || '''f(x) = x²''' || '''h(x) = x³'''
|}
{{Arbeiten|NUMMER=1|ARBEIT=
# Vergleiche den Graph der Funktion mit h(x) = x<sup>3</sup> mit dem Graphen der Funktion g(x) = x. Beschreibe Gemeinsamkeiten und Unterschiede!
# Vergleiche den Graph der Funktion mit h(x) = x<sup>3</sup> mit dem Graphen der quadratischen Funktion mit f(x) = x<sup>2</sup>. Beschreibe Gemeinsamkeiten und Unterschiede!
# Vergleiche den Graph der Funktion mit h(x) = x<sup>3</sup> mit dem Graphen der quadratischen Funktion mit f(x) = x<sup>2</sup>. Beschreibe Gemeinsamkeiten und Unterschiede!
}}
|3=Arbeitsmethode}}




===Die Graphen und ein Wanderer===
===Die Graphen und ein Wanderer===
{{Arbeiten|NUMMER=2|ARBEIT=
 
# Ein Wanderer geht legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W<sub>1</sub>, W<sub>2</sub>, W<sub>3</sub>. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.}}
 
{{Box|1=Aufgabe 2|2=
[[Bild:wanderer2.png |350px]]
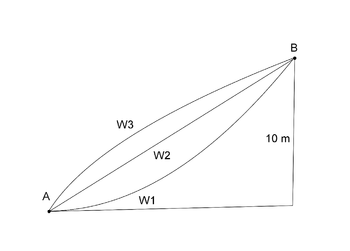
# Ein Wanderer legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W<sub>1</sub>, W<sub>2</sub>, W<sub>3</sub>. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.
|3=Arbeitsmethode}}
 
 




===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2===
===Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2===


{| class="prettytable" cellspacing="10"
{{Box|1=Aufgabe 3|2=
|-
[[Bild:alle3graphen.jpg|200px|right]]
|rowspan=3|<br>|| rowspan=3|[[Bild:alle3graphen.jpg]]|| align="center"|'''g(x) = x (Graph A)'''<br><br>
Es gilt:<br>
'''f(x) = x<sup>2</sup> (Graph B)'''<br><br>'''h(x) = x<sup>3</sup> (Graph C)'''
'''g(x) = x (Graph A)'''<br>
|-
'''f(x) = x<sup>2</sup> (Graph B)'''<br>
|align="left" | {{Arbeiten|NUMMER=3|ARBEIT=
'''h(x) = x<sup>3</sup> (Graph C)'''
 
Ergänze die Tabelle:
 
{{{!}} class="wikitable"
{{!}}-
! '''x''' !!  '''Graph A'''  !!  '''Graph B'''  !!  '''Graph C'''
{{!}}-
{{!}} 0 {{!}}{{!}}  {{!}}{{!}}  {{!}}{{!}} 
{{!}}-
{{!}} 0,2 {{!}}{{!}} {{!}}{{!}}  {{!}}{{!}} 
{{!}}-
{{!}} 0,4 {{!}}{{!}}  {{!}}{{!}}  {{!}}{{!}} 
{{!}}-
{{!}} ... {{!}}{{!}}  {{!}}{{!}}  {{!}}{{!}} 
{{!}}-
{{!}} ... {{!}}{{!}}  {{!}}{{!}}  {{!}}{{!}} 
{{!}}-
{{!}} 2 {{!}}{{!}}  {{!}}{{!}}  {{!}}{{!}} 
{{!}}}
 
 
# Begründe mit Hilfe der Tabelle, warum die '''Graphen A''' und '''B''' in der Umgebung des Nullpunktes stärker steigen als der '''Graph C'''.
# Begründe mit Hilfe der Tabelle, warum die '''Graphen A''' und '''B''' in der Umgebung des Nullpunktes stärker steigen als der '''Graph C'''.
# Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph A'''?
# Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph A'''?
# Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph B'''?}}
# Ab welchem Punkt steigt der '''Graph C''' stärker als der '''Graph B'''?
|-
|3=Arbeitsmethode}}
|align="center"|
 
{| class="prettytable"
|-
| '''x''' || '''Graph A''' || '''Graph B''' || '''Graph C'''
|-
| 0 ||<br>||<br>||<br>
|-
| 0,2 ||<br>||<br>||<br>
|-
| 0,4 ||<br>||<br>||<br>
|-
| ... ||<br>||<br>||<br>
|-
| ... ||<br>||<br>||<br>
|-
| 2 ||<br>||<br>||<br>
|-
|}
|}


== Verändern von Variablen ==
== Verändern von Variablen ==
Zeile 58: Zeile 66:
===Der Graph der Funktion h<sub>a</sub>(x)<math>= a \cdot x^3</math> ===
===Der Graph der Funktion h<sub>a</sub>(x)<math>= a \cdot x^3</math> ===


{| class="prettytable" cellspacing="10"
{{Box|1=Aufgabe 5|2=
|-
Betätige den Schieberegler um die '''Variable a''' zu verändern. Beschreibe die Veränderung der Graphen der Funktion mit <math>f_a= a \cdot x^3</math> in Abhängigkeit von a!
|<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true"
filename="1_ax3.ggb" />
|| {{Arbeiten|NUMMER=5|ARBEIT=
Betätige den Schieberegler um die '''Variable a''' zu verändern. Beschreibe die Veränderung der Graphen der Funktion <math>f_a= a \cdot x^3</math> in Abhängigkeit von a!
}}<br>
|}


<ggb_applet height="450" width="900" showMenuBar="false" showResetIcon="true" id="z8hu2ag2" />
|3=Arbeitsmethode}}


===Der Graph der Funktion h<sub>a,c</sub>(x)<math>  = a \cdot x^3 + c</math>===
===Der Graph der Funktion h<sub>a,c</sub>(x)<math>  = a \cdot x^3 + c</math>===
<br>
 
{| class="prettytable" cellspacing="10"
{{Box|1=Aufgabe 6|2=
|-  
Verändere - mit dem Schieberegler - den Wert der '''Variablen c'''. Beschreibe!
|<ggb_applet height="300" width="400" showMenuBar="false" showResetIcon="true"  
 
filename="2_ax3c.ggb" />
<ggb_applet height="450" width="900" showMenuBar="false" showResetIcon="true" id="qkvyjrqg" />
|| {{Arbeiten|NUMMER=6|ARBEIT=
|3=Arbeitsmethode}}
Verändere - mit dem Schieberegler - den Wert der '''Variablen c'''. Beschreibe!}}<br>
|}


==Teste Dein Wissen==
==Teste Dein Wissen==
[http://brinkmann-du.de/mathe/rbtest/2puzzle/fkt_erkennen_001.htm Ordne die Funktionsterme den Funktionsgraphen zu!]


[http://www.mathe-online.at/tests/fun1/erkennen.html Ordne die Funktionsterme den Funktionsgraphen zu! (auf www.mathe-online.at)]


{{Autoren|[[Benutzer:Hans-Georg Weigand|Hans-Georg Weigand]], [[Benutzer:Michael Schuster|Michael Schuster]], [[Benutzer:Jan Wörler|Jan Wörler]]und [[Benutzer:Petra Bader|Petra Bader]]}}
{{Fortsetzung|weiter=Weiter|weiterlink=Potenzfunktionen - 1. Stufe}}

Aktuelle Version vom 2. November 2018, 21:11 Uhr

Potenzfunktionen Mathematik-digital.de

Einführung

Die Graphen der Funktionen x, x² und x³

Aufgabe
Graphx.jpg
Xhoch2.jpg
Graphxhoch3.jpg
  1. Vergleiche den Graph der Funktion h(x) = x3 mit dem Graphen der Funktion g(x) = x. Beschreibe Gemeinsamkeiten und Unterschiede!
  2. Vergleiche den Graph der Funktion mit h(x) = x3 mit dem Graphen der quadratischen Funktion mit f(x) = x2. Beschreibe Gemeinsamkeiten und Unterschiede!


Die Graphen und ein Wanderer

Aufgabe 2

Wanderer2.png

  1. Ein Wanderer legt bei seinem Weg von A nach B einen Höhenunterschied von 10 m zurück. Wir betrachten nun drei verschiedene Formen des Verbindungsweges. Diese drei Wege haben im Seitenprofil in etwa die eingezeichneten Formen W1, W2, W3. Beschreibe den Wanderweg jeweils entlang dieser drei Wege, den der Wanderer zurücklegt, wenn er von A nach B geht.



Wir betrachten jetzt die drei Funktionen mit ihren Graphen im Bereich von x = 0 bis x = 2

Aufgabe 3
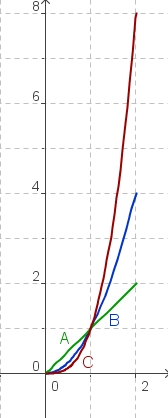
Alle3graphen.jpg

Es gilt:
g(x) = x (Graph A)
f(x) = x2 (Graph B)
h(x) = x3 (Graph C)

Ergänze die Tabelle:

x Graph A Graph B Graph C
0
0,2
0,4
...
...
2


  1. Begründe mit Hilfe der Tabelle, warum die Graphen A und B in der Umgebung des Nullpunktes stärker steigen als der Graph C.
  2. Ab welchem Punkt steigt der Graph C stärker als der Graph A?
  3. Ab welchem Punkt steigt der Graph C stärker als der Graph B?


Verändern von Variablen

Der Graph der Funktion ha(x)

Aufgabe 5

Betätige den Schieberegler um die Variable a zu verändern. Beschreibe die Veränderung der Graphen der Funktion mit in Abhängigkeit von a!

GeoGebra

Der Graph der Funktion ha,c(x)

Aufgabe 6

Verändere - mit dem Schieberegler - den Wert der Variablen c. Beschreibe!

GeoGebra

Teste Dein Wissen

Ordne die Funktionsterme den Funktionsgraphen zu! (auf www.mathe-online.at)

Weiter
Abgerufen von „https://unterrichten.zum.de/index.php?title=Potenzfunktionen_-_Einführung&oldid=69124“