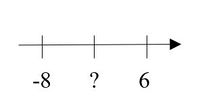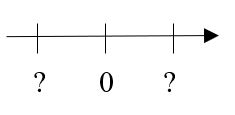Einführung in die Negativen Zahlen/Erweiterung der Zahlengeraden: Unterschied zwischen den Versionen
Main>Karl Kirst K (Aufgabe float -> Aufgabe) |
KKeine Bearbeitungszusammenfassung |
||
| (19 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken | |||
|{{Einführung in die Negativen Zahlen}} | |||
|Lernschritte einblenden | |||
|Lernschritte ausblenden | |||
}} | |||
<br> | |||
<p align="center"> | |||
<iframe width="560" height="315" src="https://www.youtube.com/embed/3xguJ0hg7mE?rel=0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | <iframe width="560" height="315" src="https://www.youtube.com/embed/3xguJ0hg7mE?rel=0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | ||
< | </p> | ||
{| | |||
| | {{Box | ||
|Titel= Frage | |||
|Inhalt= Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null? | |||
|Klasse=Frage | |||
}} | |||
<iframe width="560" height="315" src="https://www.youtube.com/embed/ | |||
<p align="center"> | |||
<iframe width="560" height="315" src="https://www.youtube.com/embed/IZafQgQV5TY?rel=0" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | |||
</p> | |||
<p align="center"> | |||
<iframe src="https://learningapps.org/watch?v=pafmickxt18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pafmickxt18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
</p> | |||
{{ | |||
{{Box|Protokollieren|Betrachtet das Merkekästchen. Ordnet den Satzanfängen das richtige Satzende zu und übernehmt die Sätze dann auf euer Protokoll.|Arbeitsmethode}} | |||
{{Merke| | |||
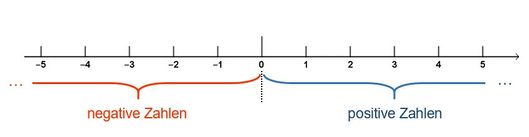
Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden.<br> | {{Box|1=Merke|2=Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden.<br> | ||
[[Datei:Zahlengerade2.JPG|600px|links]] | |||
< | [[Datei:Zahlengerade2.JPG|600px|links]] <br> | ||
<div class="lueckentext-quiz"> | |||
Die negativen Zahlen liegen '''links von der Null'''. | |||
Die positiven Zahlen liegen '''rechts von der Null'''. | |||
Die Null liegt '''in der Mitte'''. | |||
</div> | |||
|3=Merksatz}} | |||
<br><br> | |||
{{Box|Übung|Bearbeitet die folgenden Aufgaben.|Üben}} | |||
{{Box| 1.Aufgabe|<b>Findet zu jeder Situation eine passende ganze Zahl. Ordnet die Situation an die richtige Stelle auf der Zahlengeraden.</b> | |||
<br><br> | <br><br> | ||
<iframe src="https://learningapps.org/watch?v=pyc1b4ahn18" style="border:0px;width:75%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pyc1b4ahn18" style="border:0px;width:75%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
<br><br>|Arbeitsmethode}} | |||
{{Box|1=2.Aufgabe|2=<b>Welche Zahl liegt in der Mitte zwischen -8 und 6? Benutzt die Zahlengerade, um die Aufgabe zu lösen. Beschreibt auf dem Protokoll, wie ihr die Aufgabe gelöst habt.</b> | |||
<br><br> | <br><br> | ||
< | <div class="grid"> | ||
<br> | <div class="width-1-2">[[Datei:Aufgabe_Mitte.JPG|200px]]</div> | ||
<div class="width-1-2">{{Lösung versteckt|-1 liegt in der Mitte zwischen -8 und 6.|Lösung anzeigen|Lösung verbergen}}</div> | |||
</div> | |||
|3=Arbeitsmethode}} | |||
<iframe src="https://learningapps.org/watch?v=pn6cw32dn18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe><ref>übernommen und erweitert aus: mathe.delta - Berlin/Brandenburg (2016), Bamberg: C.C. Buchner, S. 19</ref> | |||
Welche Zahl liegt genau in der Mitte der angegebenen Zahlen?<ref>in Anlehnung an: mathe.delta - Berlin/Brandenburg (2016), Bamberg: C.C. Buchner, S. 19</ref><br>(Die Sternchen-Aufgaben sind schwerer als die anderen.)<br><br> | {{Box|1=3.Aufgabe|2=<b>Von den beiden folgenden Aufgaben könnt ihr eine auswählen. Die linke Aufgabe ist etwas leichter als die rechte Aufgabe. Für beide Aufgaben könnt ihr die Zahlengerade benutzen.</b> | ||
<br><br> | |||
<div class="grid"> | |||
<div class="width-1-2"><iframe src="https://learningapps.org/watch?v=pn6cw32dn18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe><ref>übernommen und erweitert aus: mathe.delta - Berlin/Brandenburg (2016), Bamberg: C.C. Buchner, S. 19</ref></div> | |||
<div class="width-1-2">Welche Zahl liegt genau in der Mitte der angegebenen Zahlen?<ref>in Anlehnung an: mathe.delta - Berlin/Brandenburg (2016), Bamberg: C.C. Buchner, S. 19</ref><br>(Die Sternchen-Aufgaben sind schwerer als die anderen.)<br><br> | |||
a) 7 und 17<br> | a) 7 und 17<br> | ||
b) -8 und 0<br> | b) -8 und 0<br> | ||
| Zeile 40: | Zeile 71: | ||
<nowiki>*</nowiki>e) -100 und -36<br> | <nowiki>*</nowiki>e) -100 und -36<br> | ||
<nowiki>*</nowiki>f) -28 und 12<br> | <nowiki>*</nowiki>f) -28 und 12<br> | ||
{{Lösung versteckt|Die gesuchte Zahl muss zu beiden Zahlen denselben Abstand haben.|Tipp anzeigen|Tipp ausblenden}} | |||
Die gesuchte Zahl muss zu beiden Zahlen denselben Abstand haben. | {{Lösung versteckt|a) 12 b) -4 c) 2 d) 2 e) -68 f) -8|Lösung anzeigen|Lösung verbergen}} | ||
</div> | |||
</div> | |||
|3=Arbeitsmethode}} | |||
a) 12 b) -4 c) 2 d) 2 e) -68 f) -8 | |||
</ | |||
|} | |||
=== Entgegengesetzte Zahlen und Betrag === | === Entgegengesetzte Zahlen und Betrag === | ||
<br> | <br> | ||
< | {{Box|1=Kommunizieren und Protokollieren|2= | ||
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann.</ | <div class="grid"> | ||
< | <div class="width-1-2">[[Datei:Mitte zwischen zwei Zahlen.JPG|links]]</div> | ||
<div class="width-1-2">Welche Zahlen könnt ihr für die Fragezeichen einsetzen? Löst und begründet eure Antwort auf dem Protokoll.</div> | |||
</div> | |||
{{Lösung versteckt|Man kann für die Fragezeichen alle Zahlen einsetzen, die sich nur durch das Vorzeichen unterscheiden, also z.B. -3 & 3, -18 & 18, -5 & 5,… , da diese Zahlenpaare denselben Abstand zur 0 haben.|Lösung anzeigen|Lösung verbergen}} | |||
|3=Arbeitsmethode}} | |||
{{Box|Protokollieren| | |||
# Lest euch das Merkekästchen gut durch. | |||
# Löst die Aufgaben in den Learning Apps. | |||
# Notiert auf eurem Protokoll <b>drei</b> Beispiele zu entgegengesetzten Zahlen und <b>zwei</b> Beispiele zum Betrag. Ihr könnt Beispiele aus den Aufgaben nehmen.|Arbeitsmethode}} | |||
{{Box|1=Merke|2=* Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen <b>entgegengesetzte Zahlen</b>. | |||
* Der Abstand einer Zahl zur 0 heißt <b>Betrag</b> und wird mit Betragsstrichen gekennzeichnet, z.B. <nowiki>|</nowiki>-4<nowiki>|</nowiki> = 4; <nowiki>|</nowiki>+4<nowiki>|</nowiki> = 4.|3=Merksatz}} | |||
===Weitere Erklärungen zum Betrag=== | |||
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann. Der Betrag der 0 ist 0, da man ja keine Schritte mehr laufen muss, um zur 0 zu gelangen. | |||
<br><br> | |||
{{Box|Übung zu den entgegengesetzten Zahlen|<iframe src="https://learningapps.org/watch?v=pgaigrjva18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|Üben}} | |||
{{Box|Übung zum Betrag|<iframe src="https://learningapps.org/watch?v=pwi8rq6bj18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|Üben}} | |||
{{Box|1=Kommunizieren und Protokollieren|2= | |||
<div class="grid"> | |||
<div class="width-1-2"> | |||
An manchen analogen Thermometern findet man bei den Zahlen unter 0 kein Minuszeichen. Findet gemeinsam mindestens einen Grund dafür und mindestens einen Grund dagegen, das Minuszeichen auf Thermometern mitzuschreiben.</div> | |||
<div class="width-1-2">[[Datei:Thermometer.jpg|miniatur|Ein analoges Thermometer]]</div> | |||
</div> | |||
|3=Arbeitsmethode}} | |||
{{Fortsetzung|weiter=Weiter|weiterlink=../Ordnen_von_negativen_Zahlen}} | |||
[[Kategorie:Einführung in die Negativen Zahlen]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:LearningApps]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 18. Februar 2024, 23:14 Uhr
Findet zu jeder Situation eine passende ganze Zahl. Ordnet die Situation an die richtige Stelle auf der Zahlengeraden.
Von den beiden folgenden Aufgaben könnt ihr eine auswählen. Die linke Aufgabe ist etwas leichter als die rechte Aufgabe. Für beide Aufgaben könnt ihr die Zahlengerade benutzen.
(Die Sternchen-Aufgaben sind schwerer als die anderen.)
a) 7 und 17
b) -8 und 0
c) -8 und 12
d) -2 und 6
*e) -100 und -36
*f) -28 und 12
Entgegengesetzte Zahlen und Betrag
- Lest euch das Merkekästchen gut durch.
- Löst die Aufgaben in den Learning Apps.
- Notiert auf eurem Protokoll drei Beispiele zu entgegengesetzten Zahlen und zwei Beispiele zum Betrag. Ihr könnt Beispiele aus den Aufgaben nehmen.
- Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen entgegengesetzte Zahlen.
- Der Abstand einer Zahl zur 0 heißt Betrag und wird mit Betragsstrichen gekennzeichnet, z.B. |-4| = 4; |+4| = 4.
Weitere Erklärungen zum Betrag
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann. Der Betrag der 0 ist 0, da man ja keine Schritte mehr laufen muss, um zur 0 zu gelangen.