Potenzfunktionen - 4. Stufe: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
__NOTOC__ | __NOTOC__ | ||
== Die Graphen der Funktionen mit f(x) = x<sup>-1/n</sup>, n <small>∈</small> IN<sup>*</sup> == | ==Die Graphen der Funktionen mit f(x) = x<sup>-1/n</sup>, n <small>∈</small> IN<sup>*</sup>== | ||
=== Vergleich mit Funktionen aus Stufe 3 === | ===Vergleich mit Funktionen aus Stufe 3=== | ||
<ggb_applet height="450" width="900" | <ggb_applet height="450" width="900" showmenubar="false" showreseticon="true" id="xhhysjna" /> | ||
{{Box|1=Aufgabe 1|2= | {{Box|1=Aufgabe 1|2= | ||
| Zeile 21: | Zeile 21: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
== Exponenten, Brüche und Potenzgesetze == | ==Exponenten, Brüche und Potenzgesetze== | ||
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponenten. Denke dabei insbesondere an folgenden Zusammenhang: | Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponenten. Denke dabei insbesondere an folgenden Zusammenhang: | ||
:''Für eine reelle Zahl a und eine natürliche Zahl n<math>\neq</math>0 wird definiert:'' | :''Für eine reelle Zahl a und eine natürliche Zahl n<math>\neq</math>0 wird definiert:'' | ||
:<math>a^{-n} := \textstyle \frac{1}{a^n}</math> für <math>a \neq 0.</math> | :<math>a^{-n} := \textstyle \frac{1}{a^n}</math> für <math>a \neq 0.</math> | ||
| Zeile 29: | Zeile 30: | ||
Auf unsere Situation angewandt ergibt sich: | Auf unsere Situation angewandt ergibt sich: | ||
:<font style="vertical-align:0%;"><math>x^{-\frac 1 n}</math></font><math>= \frac{1}{x^{\frac 1 n}}.</math> | :<font style="vertical-align:0%;"><math>x^{-\frac 1 n}</math></font><math>= \frac{1}{x^{\frac 1 n}}.</math> | ||
| Zeile 42: | Zeile 44: | ||
== Potenzfunktionen und ihre Umkehrfunktionen == | ==Potenzfunktionen und ihre Umkehrfunktionen== | ||
<big>'''Beispiel I:'''</big> | <big>'''Beispiel I:'''</big> | ||
| Zeile 49: | Zeile 51: | ||
<math>g^{\,-1}</math> ergibt sich aus <math>\!\,g</math> durch Auflösen nach <math>\!\,x</math>. Es ist:<br /> | <math>g^{\,-1}</math> ergibt sich aus <math>\!\,g</math> durch Auflösen nach <math>\!\,x</math>. Es ist:<br /> | ||
<math> | <math>\begin{array}{lcr} x^{\frac{1}{3}} & = & g(x) = y \\ x^{\frac{3}{3}} & = & y^3 \\ x & = & y^3 \end{array}</math> | ||
\begin{ | |||
= | |||
\end{ | |||
</math> | |||
Vertauschen von x und y ergibt schließlich die gesuchte Funktion: f(x)<math>=</math>x<sup>3</sup>. | Vertauschen von x und y ergibt schließlich die gesuchte Funktion: f(x)<math>=</math>x<sup>3</sup>. | ||
<ggb_applet height="450" width="900" | <ggb_applet height="450" width="900" showmenubar="false" showreseticon="true" id="uxgafbxh" /> | ||
<big>'''Beispiel II:'''</big> | <big>'''Beispiel II:'''</big> | ||
| Zeile 66: | Zeile 61: | ||
Auflösen nach x ergibt:<br /> | Auflösen nach x ergibt:<br /> | ||
<math> | |||
\begin{ | <math>\begin{array}{lcr} y & = & x^{-\frac{1}{3}} \\ y^3 & = & x^{- \frac{3}{3}} \\ & = & x^{-1} \\ y^3 & = & \frac{1}{x} \\ x \cdot y^3 & = & 1 \\ | ||
y = x^{- \frac 1 3} | x & = & \frac{1}{y^3}\\ & = & y^{-3} \end{array}</math> | ||
y^3 = x^{- \frac 3 3} \\ | |||
= x^{-1} \\ | |||
= \frac 1 x | |||
x \cdot y^3 = 1 | |||
x = \frac{1}{y^3} \\ | |||
= y^{-3} | |||
\end{ | |||
</math> | |||
<ggb_applet height="450" width="900" | <ggb_applet height="450" width="900" showmenubar="false" showreseticon="true" id="sukyfev6" /> | ||
''Hinweis: Man beachte besonders hier die unterschiedliche Bedeutung von f<sup>-1</sup> und f(x)<math>=</math>x<sup>-1</sup>!'' | ''Hinweis: Man beachte besonders hier die unterschiedliche Bedeutung von f<sup>-1</sup> und f(x)<math>=</math>x<sup>-1</sup>!'' | ||
=== Vergleich mit Potenzfunktionen der Stufe 1 === | ===Vergleich mit Potenzfunktionen der Stufe 1=== | ||
Im Zusammenhang mit den Umkehrfunktionen dieser Art kann es sinnvoll sein, sich die Potenzfunktionen der Stufe 1 noch einmal vor Augen zu führen. [[Potenzfunktionen_-_1._Stufe |Hier kannst Du direkt zur Stufe 1 springen]]. | Im Zusammenhang mit den Umkehrfunktionen dieser Art kann es sinnvoll sein, sich die Potenzfunktionen der Stufe 1 noch einmal vor Augen zu führen. [[Potenzfunktionen_-_1._Stufe |Hier kannst Du direkt zur Stufe 1 springen]]. | ||
| Zeile 96: | Zeile 83: | ||
<br /> | <br /> | ||
=== Zusammenfassung === | ===Zusammenfassung=== | ||
Die Umkehrfunktionen von Potenzfunktionen der Form <font style="vertical-align:15%;"><math>f(x) = x^{\frac 1 n},</math> mit n ∈ IN<sup>*</sup> und <math>n\geq2</math></font> sind Potenzfunktionen der Form <math>f(x)\!\, = x^n.</math> Sie sind definiert auf dem Definitionsbereich D = IR<sup>+</sup><sub>0</sub>.<br /> | Die Umkehrfunktionen von Potenzfunktionen der Form <font style="vertical-align:15%;"><math>f(x) = x^{\frac 1 n},</math> mit n ∈ IN<sup>*</sup> und <math>n\geq2</math></font> sind Potenzfunktionen der Form <math>f(x)\!\, = x^n.</math> Sie sind definiert auf dem Definitionsbereich D = IR<sup>+</sup><sub>0</sub>.<br /> | ||
| Zeile 103: | Zeile 90: | ||
== *Zusammenfassung: Was bewirken Parameter in Potenzfunktionen? - Merkregel "5 S"-Prinzip == | ==*Zusammenfassung: Was bewirken Parameter in Potenzfunktionen? - Merkregel "5 S"-Prinzip== | ||
<small>(* Bearbeitung freiwillig, Ergänzung)</small> | <small>(* Bearbeitung freiwillig, Ergänzung)</small> | ||
<ggb_applet height="450" width="900" | <ggb_applet height="450" width="900" showmenubar="false" showreseticon="true" id="ju6exjps" /> | ||
{{Box|1=Aufgabe 4|2= | {{Box|1=Aufgabe 4|2= | ||
| Zeile 122: | Zeile 109: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
== *Zum Weiterdenken: Mit Funktionen malen == | ==*Zum Weiterdenken: Mit Funktionen malen== | ||
<small>(freiwillig)</small> | <small>(freiwillig)</small> | ||
| Zeile 157: | Zeile 144: | ||
[[Kategorie:Mathematik]] | [[Kategorie:Mathematik]] | ||
[[Kategorie:Interaktive Übung]] | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie: | [[Kategorie:Analysis]] | ||
[[Kategorie:Potenzfunktionen]] | |||
Aktuelle Version vom 24. April 2022, 10:36 Uhr
Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN*
Vergleich mit Funktionen aus Stufe 3

Vergleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 3 dieses Kurses kennst (rot strichliert); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.
- Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
- Definitionsbereich
- Symmetrie
- Monotonie
- größte und kleinste Funktionswerte
- Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen
- Die Definitionsbereiche der roten und blauen Funktionen sind für n>1 nicht-negativ. Im Definitionsbereich der blauen Funktionen muss ferner auch die 0 ausgeschlossen werden. Die verschiedenen blauen Graphen sind streng-monoton fallend. Rote und blaue Graphen haben alle den Punkt (1,1) gemeinsam (Begründung: 1r 1 für alle ). Der Wertebereich der blauen Graphen ist ]0,∞[.
Exponenten, Brüche und Potenzgesetze
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponenten. Denke dabei insbesondere an folgenden Zusammenhang:
- Für eine reelle Zahl a und eine natürliche Zahl n0 wird definiert:
- für
Auf unsere Situation angewandt ergibt sich:
Überprüfe die folgende Behauptung auf Richtigkeit und begründe Deine Entscheidung:
Es sei n eine natürliche Zahl; dann hat die Funktion
den Definitonsbereich D = IR+.
- Nach Stufe 3 dieses Kurses ist eine Wurzelfunktion für nur auf IR+o definiert, das heißt ihr Definitionsbereich
- Aufgrund des Zusammenhangs überträgt sich der Definitionsbereich der Funktion g grundsätzlich auf die Funktion f. Einschränken muss man den Definitionsbereich von f allerdings noch um jene Werte, bei denen g(x)0 gilt, also um x0. Damit ergibt sich für den Definitionsbereich der Funktion f: DIR+.
Potenzfunktionen und ihre Umkehrfunktionen
Beispiel I: Es sei g eine Potenzfunktion, definiert auf D = IR+0 durch . Gesucht ist die Umkehrfunktion von .
ergibt sich aus durch Auflösen nach . Es ist:
Vertauschen von x und y ergibt schließlich die gesuchte Funktion: f(x)x3.

Beispiel II: Es sei f eine Potenzfunktion, nun definiert durch mit dem Definitionsbereich D = IR+. Gesucht ist wieder ihre Umkehrfunktion f-1.
Auflösen nach x ergibt:

Hinweis: Man beachte besonders hier die unterschiedliche Bedeutung von f-1 und f(x)x-1!
Vergleich mit Potenzfunktionen der Stufe 1
Im Zusammenhang mit den Umkehrfunktionen dieser Art kann es sinnvoll sein, sich die Potenzfunktionen der Stufe 1 noch einmal vor Augen zu führen. Hier kannst Du direkt zur Stufe 1 springen.
Zu welchen vorgegebenen Potenzfunktionen gibt es eine Umkehrfunktion? Welche Eigenschaften muss die gegebene Potenzfunktion erfüllen, damit es eine Umkehrfunktion gibt?
Begründe Deine Überlegungen und beachte dabei besonders Definitions- und Wertebereich der betrachteten Funktionen, sowie ihr Monotonieverhalten!
Ähnliches gilt für Funktionen der Form mit auf dem Definitionsbereich . Hier lautet die Umkehrfunktion f(x)x-n.
Hat man aber eine Potenzfunktion f(x)xn mit (also eine aus der Stufe 1 dieses Lernpfades) vorgegeben, so ist sie - für gerade n - auf ihrem Defintionsbereich nicht überall streng monoton. Die Umkehrbarkeit ist aber nur auf streng monotonen Intervallen möglich. Betrachtet man f auf dem eingeschränkten Definitionsbereich , so ist sie dort streng monoton und damit umkehrbar. Die Umkehrfunktion ist dort .
Zusammenfassung
Die Umkehrfunktionen von Potenzfunktionen der Form mit n ∈ IN* und sind Potenzfunktionen der Form Sie sind definiert auf dem Definitionsbereich D = IR+0.
Die Umkehrfunktionen von Potenzfunktionen der Form mit n ∈ IN* und sind Potenzfunktionen der Form . Sie sind definiert auf dem Definitionsbereich D = IR+.
*Zusammenfassung: Was bewirken Parameter in Potenzfunktionen? - Merkregel "5 S"-Prinzip
(* Bearbeitung freiwillig, Ergänzung)

Schau Dir dieses Video (Link hier) auf www.oberprima.com an. Dort lernst Du die Merkregel des "5 S"-Prinzips kennen; die "5 S" lauten:
- Spiegeln
- Strecken
- Stauchen
- Schieben
- Superponieren
Beantworte nun die folgenden Fragen:
- Wie findest Du das Video? Was macht der Vortragende gut, welche Fehler macht er?
- Welche der genannten Veränderungen kannst Du mit dem Applet erzielen? Welche der Parameter sind für welche Veränderung verantwortlich?
- Wo gehen die Variationsmöglichkeiten des Applets über die im Video vorgestellten hinaus?
*Zum Weiterdenken: Mit Funktionen malen
(freiwillig)

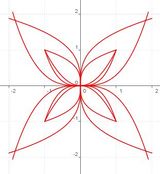
Das obenstehende Bild ist vollständig aus Potenzfunktionen der Form
mit zusammengesetzt.
Bearbeite zu dem Bild die folgenden Fragen:
- Auf welchen Intervallen sind die Funktionen jeweils definiert?
- Das "Blatt" rechts oben im Bild ist aus drei verschiedenen Potenzfunktionen aufgebaut.
Untersuche, wie die Parameter a und q die Graphen beeinflussen und welche Werte für a und q hier verwendet sind. - Von welcher Form sind die Funktionen, die das Blatt links unten ausbilden?
- Wie kann man die Größe der Blätter beeinflussen?
- Auf welchen Abschnitten sind die Funktionen definiert?
Und nun geht's zum Abschlusstest