Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Potenzfunktionen - Test: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Michael Schuster (Quiz geändert) |
Keine Bearbeitungszusammenfassung |
||
| (28 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Lernpfad Potenzfunktionen}}|Lernschritte einblenden|Lernschritte ausblenden}} | |||
__NOTOC__ | |||
{{Box|1=Übung|2= | |||
Hier kannst Du Dein Wissen über die Potenzfunktionen testen. | Hier kannst Du Dein Wissen über die Potenzfunktionen testen. | ||
| Zeile 5: | Zeile 9: | ||
{ Gib die Eigenschaften des Graphen an, die für die angegebenen Funktionen zutreffen. | { Gib die Eigenschaften des Graphen an, die für die angegebenen Funktionen zutreffen. | ||
| typ="()" } | | typ="()" } | ||
| achsensymmetrisch | punktsymmetrisch | | achsensymmetrisch | punktsymmetrisch | nicht symmetrisch | ||
-+ f(x)= 3 x< | -+- <math>f(x) = 3 x^3 \quad</math> | ||
- | --+ <math>g(x)= -2 x^{\frac 13}</math> | ||
+- h(x)= x< | +-- <math>h(x)= x^{-2} \quad</math> | ||
</quiz> | |||
<quiz display="simple"> | |||
{Welche Bedingungen müssen erfüllt sein, damit die Funktion <math>f(x)=a \cdot x^{z}, a \in \mathbb{R}, z \in \mathbb{Z}</math> einen kleinsten Wert besitzt?} | |||
+ a ist positiv und z ist gerade. | |||
- a ist negativ und z ist gerade. | |||
- a ist positiv und z ist ungerade. | |||
- a ist negativ und z ist ungerade. | |||
</quiz> | |||
<quiz display="simple"> | |||
{Welche Punkte liegen auf den Graphen der angegebenen Funktionen? | |||
| typ="()" } | |||
| <math>(0/0)</math> | <math>(-1/1)</math> | <math>(1/1)</math> | |||
+-- <math>f(x) = 3 x^3 \quad</math> | |||
+-- <math>g(x)= -2 x^{\frac 13}</math> | |||
--+ <math>h(x)= x^{-3} \quad</math> | |||
</quiz> | |||
<quiz display="simple"> | |||
{Für welche Funktionen ist der Definitionsbereich auf <math>\mathbb{R}^{+}_0</math> beschränkt?} | |||
- <math>f(x) = 3 x^3 \quad</math> | |||
+ <math>g(x)= -2 x^{\frac 13}</math> | |||
- <math>h(x)= x^{-3} \quad</math> | |||
</quiz> | |||
<quiz display="simple"> | |||
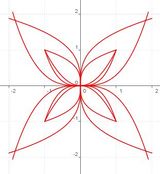
{[[Bild:potenztest1.jpg]]<br>Ordne den Graphen die entsprechenden Funktionsterme zu. | |||
| typ="()" } | |||
| a | b | c | d | e | |||
+---- <math>\frac{1}{8} x^2</math> | |||
----+ <math>x^{-\frac{1}{3}}</math> | |||
--+-- <math>2 x^3 \quad</math> | |||
---+- <math>-\frac 12 x^{\frac 12}</math> | |||
-+--- <math>x^{-3} \quad</math> | |||
</quiz> | </quiz> | ||
<quiz display="simple"> | |||
{Welche Graphen der unten stehenden Funktionen sind im Bereich <math>x \in \mathbb{R}^\mbox{+}</math> monoton steigend?} | |||
- <math>f(x)= -3 x^3 \quad</math> | |||
+ <math>g(x)= x^{\frac 13}</math> | |||
+ <math>h(x)= -x^{-2} \quad</math> | |||
</quiz> | |||
<quiz display="simple"> | <quiz display="simple"> | ||
{ | {[[Bild:potenztest2.jpg]]<br>Ordne den obigen Tabellen (mit gerundeten Werten) die entsprechenden Graphenarten zu. | ||
+ | | typ="()" } | ||
- | | G<sub>a</sub> | G<sub>b</sub> | G<sub>c</sub> | G<sub>d</sub> | G<sub>e</sub> | ||
- | -+--- Parabel | ||
- | ---+- Kubische Grundparabel | ||
--+-- Hyperbel | |||
+---- Quadratwurzel | |||
----+ Kubikwurzel | |||
</quiz> | </quiz> | ||
|3=Übung}} | |||
[[Kategorie:Mathematik]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:Analysis]] | |||
[[Kategorie:Potenzfunktionen]] | |||
Aktuelle Version vom 24. April 2022, 10:35 Uhr
Übung
Hier kannst Du Dein Wissen über die Potenzfunktionen testen.