Zentrische Streckung/Eigenschaften der zentrischen Streckung/6.Station: Unterschied zwischen den Versionen

Aktuelle Version vom 23. April 2022, 16:00 Uhr

Hier ist alles, was du bisher herausgefunden hast, zusammengefasst. Übertrage diese Zusammenfassung in dein Heft!

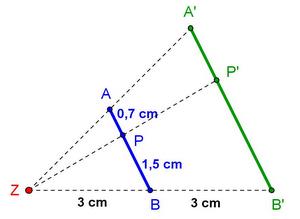
Eigenschaften der zentrischen Streckung

Jede Gerade, die durch das Zentrum Z verläuft, wird auf sich selbst abgebildet. Sie ist eine Fixgerade.
Jede Gerade, die nicht durch das Zentrum Z verläuft, wird auf eine parallele Bildgerade abgebildet. Sie ist parallelentreu.
Die Bildstrecke ist $\vert k \vert$ -mal so lang wie die Urstrecke. Sie ist also nicht längentreu.
Jedoch ist sie längenverhältnistreu.
Die zentrische Streckung ist geradentreu, winkeltreu und kreistreu.
Der Flächeninhalt der Bildfigur beträgt das $\vert k \vert^{2}$ -fache des Flächeninhalts der Urfigur. $( A_{\Delta A'B'C'} = \vert k \vert^{2} \cdot A_{\Delta ABC} )$ .
Die zentrische Streckung ist deshalb nicht flächeninhaltstreu.

@@ Zeile 19: / Zeile 19: @@
 *Jedoch ist sie '''längenverhältnistreu'''. <br>
 *Die zentrische Streckung ist '''geradentreu''', '''winkeltreu''' und '''kreistreu'''.
-*Der Flächeninhalt der Bildfigur beträgt das '''<math>\vert k \vert^{2}</math>-fache''' des Flächeninhalts der Urfigur. ('''A<sub><math>\Delta</math>A'B'C'</sub> = <math>\vert k \vert^{2} \cdot A_{\Delta ABC}</math>''')
+*Der Flächeninhalt der Bildfigur beträgt das '''<math>\vert k \vert^{2}</math>-fache''' des Flächeninhalts der Urfigur. '''<math>( A_{\Delta A'B'C'} = \vert k \vert^{2} \cdot A_{\Delta ABC} )</math>'''.
 *Die zentrische Streckung ist deshalb '''nicht''' flächeninhaltstreu.
 |3=Merksatz}}
-{{Fortsetzung|weiter=Längenverhältnistreue|weiterlink=../7.Station}}
+{{Fortsetzung|weiter=Übung|weiterlink=../7.Station}}
-[[Kategorie:Mathematik]]
-[[Kategorie:ZUM2Edutags]]
 [[Kategorie:Interaktive Übung]]
 [[Kategorie:R-Quiz]]