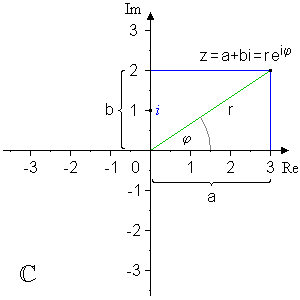Lazarus/Fraktale - Kunst aus Mathematik und Informatik

Fraktale

Mathematik kann nicht nur mit Formeln und Zahlen beindrucken; manche Zweige der Mathematik sind regelrecht künstlerisch. Das Spannende dabei ist, dass sehr einfache Rechenvorschriften und Formeln sehr komplizierte Formen hervorbringen können, wenn man sie immer und immer wieder aufs Neue anwendet ("iteriert"). Ein Beispiel dafür ist die so genannte Mandelbrotmenge (benannt nach dem Mathematiker Benoît Mandelbrot).

Ein bisschen Mathematik vorweg

Ganz ohne Mathematik geht es nicht. Macht aber auch nichts. Eigentlich ist da nichts, was man nicht mit einfach mit "plus" und "mal" rechnen könnte. Wenn man allerdings entsprechende Webseiten zur Mandelbrot-Menge anschaut, dann ist da sehr bald von komplexen Zahlen die Rede. Aber keine Angst: Das "komplex" ist nicht im Sinne von "kompliziert" zu verstehen, sondern soll "zusammengesetzt" bedeuten. Wenn Du wissen willst, wie das in etwa funktioniert, dann lies die nächsten Unterabschnitte, ansonsten kannst Du diese auch erst einmal überspringen und direkt bei "Übersetzung_in_eine_computergerechte_Fassung_mit_reellen_Zahlen" weiterlesen.

Komplexe Zahlen - ganz einfach

Imaginäre Zahlen

Vielleicht hast Du im Mathematik-Unterricht gehört, dass man die Wurzel aus der Zahl -1 nicht ziehen kann; die meisten Taschenrechner sagen dann einfach "Error" oder soetwas. Irgendwann haben sich Mathematiker gefragt: "Was wäre, wenn wir uns einfach vorstellen, $sqrt{-1}$ wäre doch eine Zahl?" Natürlich kann sie keine einfache positive oder negative Zahl sein, denn jede einfache positive oder negative Zahl würde, wenn man sie quadriert, ein positives Ergebnis liefern. Also gut: Dann bekommt sie eben einen neuen Namen, einen Namen, den bisher keine andere Zahl hat. Wir nennen sie $i$, weil sie im Grunde ein Phantasieprodukt ist, eine imaginäre Zahl ist. Es soll also gelten: $i^2=-1$.

Wenn aber $i$ eine Zahl ist, dann sind $2 \cdot i$ oder $3 \cdot i$, usw. ja auch Zahlen, denn man kann ja das Doppelte, Dreifache etc. von dieser Zahl nehmen. Auch Brüche oder andere reelle Zahlen kann man mit $i$ multiplizieren: Wenn $y$ eine reelle Zahl ist, dann ist $y \cdot i$ (auch $yi$ geschrieben) eben eine imaginäre Zahl.

Komplexe Zahlen

Nun haben es die Mathematiker noch weiter getrieben. Was wäre, wenn wir "normale" (also reelle) Zahlen und imaginäre Zahlen addieren könnten. Was wäre also $42+i$. Nun: wir können es nicht zu einer gewöhnlichen Zahl, wie wir sie bisher kannten, zusammenfassen. Wir müssen es bei $(42+i)$ belassen; die Schreibweise ist also nicht so sehr eine Rechenaufgabe sondern nun auch eine einzige Zahl, eine zusammengesetzte oder komplexe Zahl.

Anschauliche Darstellung

Anschaulich kann man sich eine solche Zahl $z=(a+bi)$ als einen Punkt in einem Koordinatensystem vorstellen, wobei man $a$ nach rechts und $b$ nach oben abträgt:

Der Formelteil $\ldots =r\cdot e^{i\varphi}$ in der Graphik muss uns hier nicht interessieren. Die Achsen des Koordinatensystems nennt man "Re" (für "Reell") und "Im" (für "Imaginär").

Rechenoperationen mit komplexen Zahlen

Für komplexe Zahlen können wir ganz einfache Rechenregeln entwerfen, die genauso aussehen, wie die "normalen" Rechenregeln aus dem Mathematikunterricht. Wir betrachten jeweils zwei komplexe Zahlen $(a+ib)$ und $(c+id)$ und rechnen damit. $a$ und $b$ sind normale Zahlen. Addition und Subtraktion sind dabei einfach: hier werden jeweils die reellen und die imaginären Anteile der Zahlen einzeln miteinander verrechnet. Etwas (aber nicht viel) komplizierter ist die Multiplikation: hier werden die Klammern eigentlich ganz normal ausmultipliziert und danach die Terme mit $i$ und die ohne $i$ danach sortiert. Wichtig ist, sich dabei zu erinnern, dass $i^2=-1$ ist.

Rechenoperation	Regel	Beispiel
Addition	$(a+ib)+(c+id)=((a+c)+(b+d)i)$	$(2+3i )+(5+27i)=(7+30i)$
Subtraktion	$(a+bi)-(c+di)=((a-c)+(b-d)i)$	$(2+3i )-(5+27i)=(-3+24i)$
Multiplikation	$(a+bi) \cdot (c+di)=(ac)+(ad)i+(bc)i+bd \cdot i^2=(ac-bd)+(ad+bc)i$	$(2+3i ) \cdot (5+27i)=((10-27)+(54+15)i)=(-17+69i)$
Spezialfall: Quadrieren	$(a+bi)^2 =a^2-b^2+2abi$	$(2+3i )^2=((4-9)+(2\cdot 2\cdot 3\cdot i)=(-5+12i)$

Definition der Mandelbrotmenge mit komplexen Zahlen

Die Mandelbrotmenge ist einfach eine Menge von komplexen Zahlen $c=a+bi$. Aber eben nicht alle solche Zahlen, sondern nur ganz bestimmte. Welche das sind, ergibt sich aus folgender Rechenvorschrift (Algorithmus):

Man nehme eine komplexe Zahl $z=x+yi$. Am Anfang ist $x=0$ und $y=0$. Nun ändern wir diese Zahl jedoch schrittweise immer mehr nach der folgenden Vorschrift:

$z_{\text{neu}}:=z^2+c$ Das machen wir nun immer und immer wieder. Für manche Werte von $c$ bleibt der Punkt $z$ im Lauf der Rechenschritte immer in der Nähe des Ursprungs. Diese Werte von $c$ sind die Mandelbrotmenge. Für andere Werte von $c$ wächst der Abstand irgendwann über den Wert 2. Dann kann man davon ausgehen, dass er sich danach in die Unendlichkeit entfernen wird. Diese Werte für $c$ gehören nicht zur Mandelbrotmenge. Der Abstand von $z=(x+yi)$, geschrieben als $|z|$ berechnet sich ganz einfach aus den beiden Werten mit $|z|=sqrt{x^2+y^2}$, also letztlich wie der ganz normale Abstand aus der neunten Klasse.

Übersetzung in eine computergerechte Fassung mit reellen Zahlen

Nimmt man die obige Definition der Mandelbrotmenge und schreibt für die Zahlen $z=(x+yi)$ und $c=(a+bi)$, dann ist die Mandelbrotmenge eine Menge von "Zahlen-Pärchen" $(a,b)$. Mit den oben genannten Rechenregeln für komplexe Zahlen ergeben sich aus den Original-Rechenvorschriften die folgenden "Computer-Rechenvorschriften":

Man startet mit zwei Variablen $x=0$ und $y=0$. Weiterhin betrachtet man zwei Variablen $a$ und $b$, die einen Punkt in einem Koordinatensystem markieren.

Nun wird folgendes immer wieder wiederholt:

• Aus den alten Variablen $x$ und $y$ werden neue errechnet:
  $x_{\text{neu}}=x^2-y^2+a$
  und
  $y_{\text{neu}}=2xy+b$
• ... und dann zurückübertragen. Dieser Zweischritt ist wichtig, denn sonst rechnet man schon mit einem neuen Wert von $x$ weiter, wo man noch den alten Wert braucht:
  $x=x_{\text{neu}}$
  und
  $y=y_{\text{neu}}$
  
• Die Anzahl der Rechenschritte wird in jedem Schleifendurchlauf mitgezählt.
• Die Wiederholung wird abgebrochen, wenn $x^2+y^2>4$ ist oder schon 50 Schleifendurchläufe erfolgt sind.

Tipps für die Umsetzung

• Der interessante Bereich für $a$ liegt zwischen -2 und 1, der interessante Bereich für $b$ liegt zwischen -1 und +1.
• Also hat man drei Einheiten nach rechts und 2 Einheiten nach oben. Eine sinnvolle Möglichkeit der Darstellung wäre also z.B. eine Image-Komponente mit einem Canvas von 300x200 Pixeln. Eine Länge von 1 in der Mathematik ist dann genau in 100 Pixel aufgeteilt.
• Die insgesamt 60000 Pixel müssen alle eingefärbt werden. Wenn nach mehr als 50 Rechenschritten noch kein quadratischer Abstand $x^2+y^2\geq 4$ erreicht ist, kann man davon ausgehen, dass das Wertepärchen $(a,b)$ zur Mandelbrot-Menge gehört: Man färbt es normalerweise schwarz ein.
• Für die anderen Pärchen, die nicht zur Mandelbrotmenge gehören, gibt es zwei Möglichkeiten:
  • Man färbt sie einfach weiß ein.
  • "Spaciger" sieht es aus, wenn man die Pixel um so heller macht, je mehr Rechenschritte gebraucht worden sind, um den quadratischen Abstand von 4 zu erreichen. Dann erreicht man den Effekt wie in der Graphik ganz oben. Diese ist tatsächlich mit einem selbstgeschriebenen Lazarus-Programm erzeugt worden.