Java/Monte-Carlo-Methode
In den achtziger Jahren besuchte ich mit einer Schulklasse eine Landesgartenschau. Am Eingang musste jeder Besucher einen Pingpong-Ball in eine Öffnung werfen, und eine große Digitalanzeige verriet dann eine nächste Näherung für die Kreiszahl p …
So mitten im Trubel konnte ich den verdutzten Schülern keine erschöpfende Erklärung bieten; außerdem ging es an diesem Tage ja auch um Pflanzen. Da es sich jedoch um eine 10.Klasse handelte, bekam ich später einen guten Aufhänger für die Behandlung von Näherungsverfahren für die Kreiszahl.
Monte-Carlo-Methode zur Bestimmung der Kreiszahl p
Mathematischer Hintergrund
Bei der Monte-Carlo-Methode approximiert man p durch sehr spektakuläre stochastische Überlegungen.
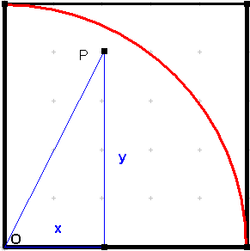
In ein Einheitsquadrat mit Einheitsviertelkreis ergießt sich ein Zufallsregen. Die Gesamtzahl g der Tropfen verhält sich zur Zahl der Tropfen im Viertelkreis v wie der Inhalt der Quadratfläche zum Inhalt der Viertelkreisfläche. Entsprechend ergibt sich folgende Näherungsgleichung:
Ein Tropfen treffe im Quadrat in P auf; ist die Streckenlänge OP kleiner oder gleich 1, befindet sich P sogar im Viertelkreis (, und der Zähler v muss erhöht werden).
Struktogramm
Java-Quelltext / For-Schleife
Die Schleife könnte man wieder mit "Solange" realisieren, wobei man vorher die Zahl der Tropfen i mit 0 initialisieren müsste; außerdem wäre dafür Sorge zu tragen, dass die Tropfenzahl i bei jedem Schleifendurchgang um eins erhöht wird und die vereinbarte Gesamtzahl g nicht übersteigt. Bequemer ist es, wenn man in einem solchen Falle die sog. For-Schleife verwendet:
// i ++ steht für das Inkrementieren von i um 1 pro Schleifendurchgang
for (int i = 1; i <= g; i++) {
//Schleifenrumpf
…
}
class Pi {
public static void main(String[] args) {
// Gesamtzahl der Tropfen
int g = Integer.parseInt(args[0]);
// Tropfen im Viertelkreis
int v = 0;
// Koordinaten des Punktes P
double x,y;
System.out.println(" Monte Carlo Methode");
System.out.println(" Naeherung fuer Pi:");
for (int i = 1; i <= g; i++) {
x = Math.random();
y = Math.random();
if (Math.hypot(x,y) <= 1)
v = v + 1;
}
double pi = 4*(double)v / g;
System.out.printf(" %d Tropfen, davon %d Tropfen im Viertelkreis, Pi etwa %g%n",g,v,pi);
}
}
Für die Koordinaten und für p benötigt man Gleitkommazahlen; diese werden durch den Datentyp double bereitgestellt.
Math.random()liefert Zufallszahlen von 0 bis (ausschließlich) 1.Math.hypot(x,y)berechnet die Streckenlänge OP (Hypotenusenlänge).- Das
floatbei der Berechnung der Näherung fürpist notwendig, da sonst eine Ganzzahldivision durchgeführt würde. - Im Formatstring ist
%gein Platzhalter für eine Gleitkommazahl.
Benutzereingaben über den Scanner
Der Benutzer soll zur Laufzeit die gewünschte Tropfenzahl eingeben können; dafür führen wir das sog. Scanner-Objekt - zunächst als "black box"- ein.
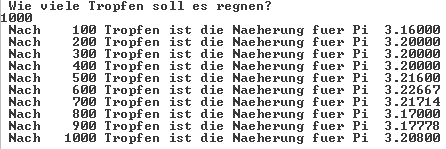
Wir interessieren uns für das Konvergenzverhalten der Monte-Carlo-Methode; deshalb lassen wir uns schon im Schleifendurchgang jeweils nach 100 Iterationsschritten den aktuellen Näherungswert ausgeben.
import java.util.Scanner;
class Pi_1 {
public static void main(String[] args) {
// Das System liest von der Standardeingabe
Scanner s = new Scanner(System.in);
System.out.println(" Wie viele Tropfen soll es regnen?");
int g = s.nextInt();
// Tropfen im Viertelkreis
int v = 0;
// Koordinaten des Punktes P
double x,y;
for (int i = 1; i <= g; i++) {
x = Math.random();
y = Math.random();
if (Math.hypot(x,y) <= 1)
v++;
double pi = 4*(float)v / i;
if (i%100 == 0)
System.out.printf(" Nach %6d Tropfen ist die Naeherung fuer Pi %g%n",i,pi);
}
}
}
Wir erkennen an dieser Stelle: Unsere Methode ist zwar sehr spektakulär, aber sie konvergiert sehr langsam …
Konvergiert das Verfahren überhaupt?
Wir müssen uns verabschieden von der Schleife vorgegebener Länge; das Verfahren soll so lange laufen, bis eine "vernünftige" Näherung erreicht ist. Aber wie realisiert man eine "Wiederhole-Schleife" in Java?
Wiederhole-Schleife
// Jetzt soll die Iteration abgebrochen werden, wenn sich die Näherungswerte
// nur noch im Rahmen eines vorgegebenen Epsilon-Bereiches ändern
class Pi_2 {
public static void main(String[] args) {
int i = 0;
int v = 0;
// Startwert von Pi für den ersten Vergleich
double pi = 3;
double x,y,pi_alt;
// Falls sich zwei Näherungswerte um höchstens diese Differenz epsi
// unterscheiden, soll die Iteration abgebrochen werden
double epsi = 1.E-5;
do {
i++; // Tropfenzahl
pi_alt = pi;
x = Math.random();
y = Math.random();
if (Math.hypot(x,y) <= 1)
v++; // Tropfen im Viertelkreis
pi = 4*(float)v / i;
}
while (Math.abs(pi_alt - pi) > epsi);
System.out.printf(" Nach %6d Tropfen ist die Naeherung fuer Pi %g%n",i,pi);
//System.out.printf(" Der Konvergenzbereich ist %g breit", 2*epsi);
}
}
Die drei Aufrufe des Programmes verdeutlichen, wie sich im Sinne des Gesetzes der großen Zahl der Wert von p herauskristallisiert; allerdings ist eine sehr große Tropfenzahl für eine vergleichsweise "bescheidene" Näherung erforderlich; das Konvergenzverhalten des Verfahrens ist also "ungünstig".
Operatoren
Außerdem kann man mit dem o.g. Quelltext auch Überraschungen erleben: Ggf. steigt das Programm z.B. mit der Meldung aus, dass es nach 2 Tropfen eine Näherung 4 für p gäbe. Wie man leicht sieht, folgt dies, wenn die ersten Tropfen alle im Viertelkreis landen.
Um auch dies zu berücksichtigen, passen wir unsere Schleifenbedingung an:
while ((Math.abs(pi_alt - pi) > epsi) || (i < 10));
Die Schleife soll also in jedem Fall für die ersten 9 Tropfen weiterlaufen; als logischen Operator haben wir || (für ODER) gewählt.
Weitere logische Operatoren sind && ( für UND) und ! (für NICHT).
An arithmetischen Operatoren haben wir bereits kennengelernt: + - * / %
Relationale Operatoren < > <= >= == !=
Runden
Wie viele Tropfen unseres Zufallsregens sind nun notwendig, um p wenigstens auf 4 Dezimalen zu bestimmen?
Ausgehend von pi = 4*(float)v / i;
kann man z.B. pi mit 10000 multiplizieren, auf Einer runden und durch 10000 dividieren.
Aus dem unteren Teil des Schleifenrumpfes würde dann
......
pi = 4*(float)v / i;
pi = Math.round(10000 * pi)/10000.0;
}
while (pi != 3.1415);
Hier verdeutlichen die 5 Aufrufe, dass sogar das verhaltene Tempo der Konvergenz sehr statistisch ist.