Java/Ulam-Folge
Wenn ich mir vornehme, eine neue Programmiersprache zu lernen, bin ich oft enttäuscht, wenn es dann am Anfang nur für das "Hallo Welt"-Programm reicht …
Das Problem bei der Einführung ist meist, dass der Autor genug mit den Besonderheiten der Syntax und der Benutzeroberfläche zu tun hat, so dass das Problem eher dienenden Charakter hat. In Wirklichkeit sind Programmiersprachen aber nur ein (austauschbares, dienendes) Werkzeug, um Probleme zu lösen.
Lassen Sie uns also ein Problem in den Mittelpunkt und die technischen Randbedingungen zurück stellen!
Ulam-Folge
Wir beginnen tatsächlich mit einem "phänomenalen Problem", die Ulam-Folge![]() :
:
- Wähle als Startzahl n eine beliebige natürliche Zahl.
- Für gerades
nentsteht das nächste Element der Folge, indem mannhalbiert. - Für ungerades
nmuss mannentsprechend verdreifachen und dann 1 addieren.
Bekanntlich (aber bis heute nicht bewiesen) hat sich durch ausgiebiges Testen ergeben, dass es für jede Startzahl n ein letztes Folgenglied gibt, und zwar 1 !!!
Obiges Ulam-Verfahren terminiert also jeweils, und das wäre in der vermuteten Allgemeingültigkeit eine wesentliche Bedingung für einen Algorithmus.
Vom Algorithmus zum Programm
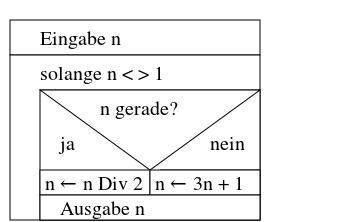
Lassen Sie uns ein Struktogramm entwickeln für diesen "Algorithmus":
- Untersuchen Sie, wie dieses Struktogramm in Java-Quelltext übertragen wird.
- Lassen Sie sich von fremdartigen Begriffen nicht irritieren, sondern versuchen Sie nur die Zusammenhänge mit dem Struktogramm zu entdecken.
class Ulam {
public static void main (String[] args) {
int n = 13;
System.out.println(n);
while(n != 1) {
if(n % 2 == 0) n = n / 2;
else n = 3*n + 1;
System.out.println(n);
}
}
}
Es ergibt sich folgende Ausgabe:
- Mit
n % 2wird der Modulo-Operator verwendet;
verwendet; n % 2liefert also den Rest bei Ganzzahldivision durch 2.
z.B.13 % 2 = 1und13 / 2 = 6 - Die Mengenklammern markieren Blöcke, wie man sie z.B. von der "BEGIN END Klammerung" bei Pascal kennt.
Dateneingabe
Da es unpraktisch ist, den Startwert n immer neu zu editieren, sieht man eine kommandozeilenorientierte Eingabe vor:
Die aktuellen Parameter werden als Zeichenketten gelesen; nach einer Leerstelle folgt der nächste Parameter; auf den ersten greift man über args[0] zu; mit Konvertierungsfunktionen kann man geeignete Übergabewerte in Zahlen umwandeln:
class Ulam {
public static void main (String[] args) {
//Der erste Parameter hat die Nummer 0
int n = Integer.parseInt(args[0]);
//Die While-Schleife klammert einen Block von Anweisungen
while(n != 1) {
if(n % 2 == 0)
n = n / 2;
else
n = 3*n + 1;
System.out.printf("%d, ",n);
}
//im Formatstring ist %d ein Platzhalter für eine ganze Zahl
}
}
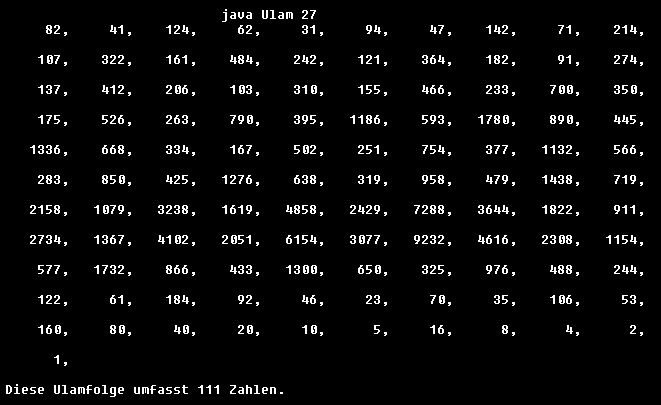
Liefert mit dem aktuellen Parameter 27:
Formatierung
Zur vernünftigen Darstellung der Ulam-Folge fehlt jetzt nur noch eine geeignete Formatierung:
class Ulam {
public static void main (String[] args) {
int n = Integer.parseInt(args[0]);
int i = 0;
while(n != 1) {
//Index für das Ulam-Folgenglied
i = i +1;
if(n % 2 == 0)
n = n / 2;
else
n = 3*n + 1;
// 7 Plätze für jede Zahl
System.out.printf("%7d,",n);
// Zeilenwechsel immer nach 10 Zahlen
if (i%10 == 0 )
System.out.println();
}
// Schleife beendet
//%n steht für einen Zeilenwechsel
System.out.printf("%n%nDiese Ulamfolge umfasst %d Zahlen.%n",i);
}
}
Problem: Finden der längsten Ulam-Folge
Man kann im Unterricht ein Problembewusstein entwickeln, dass die Termination dieser Entwicklung keinesfalls selbstverständlich ist, indem man z.B. den Term 3n + 1 durch 3n - 1 ersetzen lässt; die Schüler werden dann sehr schnell nachstehende Folgenentwicklung (und damit eine Endlosschleife) erkennen:
5, 14, 7, 20, 10, 5, 14, …
Im Wettbewerb der Gruppenarbeit ist es immer eine spannende Angelegenheit, die Startzahl zu finden, welche die längste (?) Ulam-Folge bewirkt.
Bis die Ulamfolge eine Zweierpotenz trifft, entwickeln sich oft sehr große Zahlen; im obigen Beispiel ist 9232 das größte Folgenglied.
In unserem Java-Programm ist das eine schöne Gelegenheit, auch eine einseitige Verzweigung zu berücksichtigen:
class Ulam {
public static void main (String[] args) {
int n = Integer.parseInt(args[0]);
//Zunächst wird das Maximum auf den Startwert gesetzt.
int max = n;
int i = 0;
while(n != 1) {
i = i +1;
if(n % 2 == 0)
n = n / 2;
else
n = 3*n + 1;
if (n > max)
max = n;
}
System.out.printf("%nDiese Ulamfolge umfasst %d Zahlen; %n",i);
System.out.printf("das groesste Folgenglied ist %d.%n",max);
}
}