Signifikanztest für binomialverteilte Zufallsgrößen/Grundidee vom Signifikanztest

Video 2 !

Übung 1: Grundverständnis vom Testen

Prüfe dein Verständnis zum Signifikanztest
Kreuze jeweils die richtige Antwort an!

1. Beim Signifikanztest kann man, für den bisher angenommenen Wert, die Binomialverteilung aufschreiben. Für den Fall, dass diese Verteilung gilt, treten die Werte an den Rändern der Binomialverteilung... (sehr unwahrscheinlich ein) (!sehr wahrscheinlich ein) (!nie ein) (!immer ein)

2. Tritt ein Werte im Rand der Binomialverteilung ein, so wird vermutet,... (!dass der bisherige angenommene Wert noch gilt) (dass der bisherige angenommene Wert sich verändert hat)

3. Liegt das Stichprobenergebnis im linken Rand der Binomialverteilung, so wird vermutet, dass (der wahre Wert kleiner ist, als der bisher angenommene Wert) (!der wahre Wert größer ist, als der bisher angenommene Wert)

4. Das Ziel eines Signifikanztests ist es, (der bisher angenommene Wert zu verwerfen und zu zeigen, dass sich der Wert verändert hat) (!den bisher angenommene Wert anzunehmen und zu zeigen, dass er immer noch gilt)

5. Der Verwerfungsbereich ist der Bereich, .... (indem der bisher angenommne Wert mit einer festgelegten Irrtumswahrscheinlichkeit verworfen wird) (! über den nichts ausgesagt werden darf)

6. Das Signifikanzniveau ist die maximale tolerierte Irrtumswahrscheinlichkeit dafür ... (eine Hypothese fälschlicherweise zu verwerfen) (! eine Hypothese fälschlicherweise anzunehmen)

7. Das Signifikanzniveau ist die kumulierte Wahrscheinlichkeit des ... (Verwerfungsbereichs) (! Annahmebereichs)

8. Der Annahmebereich ist der Bereich, .... (über den keine Aussage getroffen werden kann) (! indem der bisherige vermutete Wert angenommen wird)

Hast du weniger als 75% richtig, schaue dir das Video am besten nochmal an und versuche, den Test nochmal zu lösen.
Hast du 75% oder mehr richtig, kannst du weitermachen mit der nächsten Aufgabe!
Viel Spaß!

Übung 2: Vorbereitung für einen Signifikanztest

Eine Patrei sieht den Klimawandel nicht als Bedrohung an. Sie wollen daher am liebsten kein Klimaschutzprogramm in ihr Wahlprogramm aufnehmen. Aber auch sie haben die Information, dass Anfang des Jahres 2019, 71% der Menschen in Deutschland sich durch den Klimawandel bedroht gefühlt haben. Da dies kein geringer Anteil ist, beschließen sie einen Signifikanztest durchzuführen. Falls durch den Signifikanztest sich zeigen lässt, dass der Anteil im Vergleich zu Anfang des Jahres 2019 gesunken ist, wollen sie kein Klimaschutz in ihr Wahlprogramm aufnehmen.
Hilf der Partei den Signifianztest vorzubereiten!

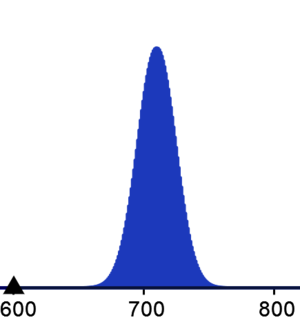
a) Skizziere die Binomialverteilung für den Fall, dass sich bei der Befragung immer noch 71% der Menschen in Deutschland durch den Klimawandel bedroht fühlen. Markiere zusätzlich den Bereich, indem die Partei vermutet, dass der Anteil geringer im Vergleich zu 2019 ist.

Bereche die Wahrscheinlichkeit dafür,...

b) dass in der Stichprobe genau 710 Menschen den Klimawandel als Bedrohung ansehen.

Nutze die Formel von Bernoulli!
Zur Berechnung nutze deinen Taschenrechner!

$P(X=710)=\tbinom{1000}{710}\cdot 0,71^{710}\cdot0,29^{290}$$=0,0278$.

Die Wahrscheinlichkeit, dass in der Stichprobe genau 710 Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,78 %.

c) Das höchstens 680 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen.

Höchtes heißt, es können 1,2,3, ...680 der Befragten den Klimawandel als Bedrohung ansehen.

Nutze zur Berechnung die Formel für die kumulierten Wahrscheinlichkeit (siehe Übung 1).
Nutze zur Berechnung deinen Taschenrechner!

$P(X\leq680)=\sum_{i=0}^{680} B_{1000,0,71} (i) = 0,0206$

Die Wahrscheinlichkeit, dass in der Stichprobe höchstens 680 der Menschen den Klimawandel als Bedrohung ansehen, beträgt 2,06. %

d) Das mindestens 740 Menschen aus der Stichprobe den Klimawandel als Bedrohung sehen.

Mindestwahrscheinlichkeiten werden über die Gegenwahrscheinlichkeit berechnet:
P(mindestens k)= 1 - P(höchstens k - 1)
Die Wahrscheinlichkeit für höchstens kannst du wieder mit dem Taschenrechner berechnen.

$P(X\geq740)=1-P(X\leq739)=0,0191$

Die Wahrscheinlichkeit, dass in der Stichprobe mindestens 740 Menschen den Klimawandel als Bedrohung ansehen, beträgt 1,91 %.

Aufbau eines Signifikanztests