Lernpfad Energie/Armbrustschießen im Weltall
Auf dieser Seite findest Du eine Art Gedankenexperiment. Sollte dir das Beispiel vielleicht ein bisschen zu sehr nach Grundschule klingen, lasse dich nicht stören: Physiker sind häufig etwas kindisch.
Eine seltsame "Hausaufgabe"
Der Weltraum – unendliche Weiten. Wir befinden uns in einer fernen Zukunft … Die Zwillinge Paul und Pauline haben bei Jugend forscht einen vierwöchigen Weltraum-Trip gewonnen, der zu mehreren Planeten und Monden des Sonnensystems führt.
Ihre Physiklehrerin, Frau Mileva, hat ihnen allerdings eine Art „Hausaufgabe“ mitgegeben: Sie sollen zwei Spielzeug-Armbrüste mit auf ihren Weltraum-Ausflug nehmen, eine große und eine kleine. Sie sollen die „universelle Wirksamkeit“ der beiden Spielzeuge bestimmen. Was sie mit „universeller Wirksamkeit“ meint, sagt sie ihnen allerdings nicht. Sie meint, als junge Forscherinnen und Forscher sollen sie sich selbst etwas überlegen.
Schuss nach oben auf Himmelskörpern
Pauline hat eine Idee:
"Wir schießen auf den verschiedenen Himmelskörpern im Universum Bolzen mit den Armbrüsten nach oben. Dann messen wir, wie hoch sie fliegen. Natürlich schreiben wir auch alles auf, was sonst noch wichtig sein könnte: Z.B. der Ortsfaktor auf den Himmelskörpern und die Masse der Bolzen. Vielleicht finden wir ja irgendeine Größe, die auf allen Himmelskörpern, also im ganzen Universum gleich ist. Dann wäre diese Größe sozusagen 'universell' "
Paul ist auch einverstanden: Auf dem Erdmond, dem Planeten Mars und auf dem Jupitermond Ganymed führen Sie sorgfältige Messungen durch. Hier eine Tabelle mit ihren Ergebnissen:
| Armbrust | Himmelskörper (Ortsfaktor g [N/kg]) | Bolzenmasse m [kg] | max. Flughöhe h [m] |
|---|---|---|---|
| klein | Mars (3,7) | 0,01 | 67,6 |
| klein | Mars (3,7) | 0,02 | 33,8 |
| klein | Erdmond (1,6) | 0,01 | 156,2 |
| klein | Erdmond (1,6) | 0,02 | 78,1 |
| klein | Ganymed (1,4) | 0,01 | 178,6 |
| klein | Ganymed (1,4) | 0,02 | 89,3 |
| groß | Mars (3,7) | 0,01 | 270,4 |
| groß | Mars (3,7) | 0,02 | 135,2 |
| groß | Erdmond (1,6) | 0,01 | 624,8 |
| groß | Erdmond (1,6) | 0,02 | 312,4 |
| groß | Ganymed (1,4) | 0,01 | 714,4 |
| groß | Ganymed (1,4) | 0,02 | 357,2 |
Paul schreibt in sein elektronisches Notizbuch einen kurzen Text über seine ersten Eindrücke. Dem Speicher ist allerdings die kosmische Höhenstrahlung nicht bekommen. Fülle die Lücken aus:
Wenn wir auf dem gleichen Himmelskörper mit der gleichen Armbrust schießen, fliegt ein schwerer Bolzen weniger hoch als ein leichter Bolzen. Wenn ich mich nicht sehr täusche, dann ist das Produkt aus der Bolzenmasse und der maximalen Flughöhe bei sonst gleichen Bedingungen immer gleich. Frau Mileva nennt so einen Zusammenhang, glaube ich, antiproportional. Noch so ein Zusammenhang besteht auch zwischen der Flughöhe und dem Ortsfaktor. Wenn ich alle Bedingungen gleich lasse und nur die Armbrust wechsle, schießt die kleine Armbrust weniger hoch. Diese Armbrust ist also wohl weniger wirksam.
Wir wollen eine universelle Formel für die Wirksamkeit finden; nennen wir die Wirksamkeit als Formelzeichen doch einfach mal . Dann müssen wir irgendwie Masse , Ortsfaktor und maximale Höhe so miteinander verrechnen, dass immer der gleiche Wert für die gleiche Armbrust herauskommt. Die drei Größen haben unterschiedliche Maßeinheiten. Die Rechenarten Plus und Minus kann man also von vornherein vergessen. Bleiben Mal und Geteilt.
Kannst Du nach Pauls Überlegungen eine Formel finden, die bei allen Zeilen der kleinen Armbrust immer wieder den gleichen Wert liefert und bei allen Zeilen der großen Armbrust auch immer nur einen einzigen Wert (jedenfalls ungefähr). Diese beiden Werte sollten natürlich unterschiedlich sein. Eigentlich ist die Lösung sehr einfach; falls Du aber nach fünf Minuten nicht darauf kommst, schau Dir mal die fertige Lösung an.
Schüsse im freien Weltraum
Während einer längeren Flugstrecke durch's All meint Paul: „Was ist, wenn Frau Mileva mit 'universell' gar nicht die verschiedenen Himmelskörpern gemeint hat, sondern die Wirksamkeit in Bereichen des Universums weit weg von jedem Himmelskörper?“ Pauline hält dagegen: „Unseren Test mit der Flughöhe können wir dann aber vergessen. Wir wissen ja, dass ohne Schwerkraft der Bolzen ewig weiterfliegen würde, wenn er nicht irgendwo anstößt.“ Paul: „Vielleicht sollten wir dann die Geschwindigkeit des Bolzens messen. Das ist ja kein Problem, wenn wir im langen Laderaum des Raumschiffs den Bolzen abschießen und die Flugzeit bis zur anderen Seite des Laderaums messen.“
Wieder stellen sie eine Tabelle auf. Die Wirksamkeit aus dem ersten Experiment schreiben sie schon einmal dazu.
| Armbrust | Wirksamkeit aus Vorgängerexperiment W [N m] | Bolzenmasse m [kg] | Geschwindigkeit v [m/s] |
|---|---|---|---|
| klein | 2,5 | 0,01 | 22,4 |
| klein | 2,5 | 0,02 | 15,8 |
| groß | 10 | 0,01 | 44,8 |
| groß | 10 | 0,02 | 31,6 |
Pauline macht sich einen Notizbucheintrag. Auch bei ihrem Gerät hat die kosmische Höhenstrahlung zugeschlagen.
Ob man es hinbekommt, auch aus den Geschwindigkeiten der verschiedenen Bolzen unsere ersten Werte für die Wirksamkeit auszurechnen. Vielleicht sollten wir zuerst einmal annehmen, dass die Wirksamkeit wieder proportional zur Bolzenmasse ist, denn das war ja auch bei unseren ersten Versuchen so. Die Formel wäre dann also irgendwas mit .
Aber bei der Geschwindigkeit wird's schwierig: Man sieht, dass bei vierfacher Wirksamkeit nur die doppelte Geschwindigkeit gemessen wird, oder anders gesagt: verdoppelt sich die Geschwindigkeit, vervierfacht sich die Wirksamkeit.
Kannst Du nach Paulines Notizbucheintrag eine passende Formel finden, die die Wirksamkeit in Abhängigkeit von der Bolzenmasse und der Geschwindigkeit des Bolzens beschreibt? Es ist nicht ganz leicht, aber probiere einfach ein bisschen herum; das machen Physiker auch häufig so. Klicke erst auf die Lösung, wenn Du entweder selbst eine sinnvoll erscheinende Lösung hast, oder mindestens 5 Minuten vergeblich herumprobiert hast.
Vorlage:Lösung versteckt mit Rand
Wo bleibt die Wirksamkeit
Auf einer langweiligen Flugstrecke stellt Pauline eine Frage, die sie schon seit ein paar Tagen umtreibt:
"Nur eine gespannte Armbrust ist doch wirksam. Wenn ich aber auf einem Planeten nach oben schieße, ist die Armbrust aber nach weniger als einer Sekunde entspannt, sie sollte also nicht mehr wirksam sein. Trotzdem fliegt der Bolzen noch weiter und weiter nach oben. Irgendwo muss die Wirksamkeit doch geblieben sein".
"Stimmt schon," meint Paul "bei der Geschwindigkeitsmessung war das einfacher. Da war der Bolzen direkt nach dem Abschuss schon schnell."
"Na, schnell war der Bolzen beim Abschuss nach oben ja zunächst auch", entgegnet Pauline, "er wurde dann halt immer langsamer, je höher der Bolzen kam".
"Kann es sein", denkt Paul laut nach, "dass die Wirksamkeit sozusagen irgendwie in der Geschwindigkeit des Bolzens steckt?“
"Und wo ist sie dann hin, als der Bolzen langsamer wurde?"
"Naja, einfach verschwunden vielleicht; verbraucht sozusagen".
"Dann ist es es aber seltsam", führt Pauline den Gedanken weiter, "dass der Bolzen dann wieder schnell nach unten kam – beinahe hätte er mich bei einem Experiment getroffen, das war richtig gefährlich. Eigentlich hatten wir doch gesagt, dass man Wirksamkeit braucht, um den Bolzen schnell zu machen. Und da oben am höchsten Punkt war ja keine andere Armbrust ...".
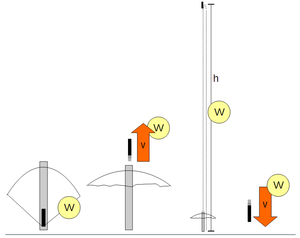
"Kann es sein, dass sich die Wirksamkeit erst in der Armbrust gesteckt hat, dann in der Geschwindigkeit des Bolzens, dann in der Höhe des Bolzens über dem Planeten, und dann wieder in der Geschwindigkeit des Bolzens?"
Er macht eine Skizze:
"Und vor dem Spannen der Armbrust?" fragt Pauline wieder
"Vorher war sie wohl in deinen oder meinen Muskeln"
"Und noch vorher?"
"Vielleicht in deinem Frühstück!"
"Apropos Frühstück. Beim Frühstück habe ich eine Funknachricht von Frau Mileva bekommen. Wir sollen in der Bordbibliothek mal schauen, was man unter altgriechisch wirksamkeit begriffsklärung findet."
Ihr habt zwar nicht die Bordbibliothek der Zukunft, aber vielleicht einen Zugriff auf's heutige Internet. Vielleicht versteckt sich ja hinter Frau Milevas Begriff der "Wirksamkeit" ein ganz anderer Begriff, wenn man ihn vom Deutschen ins klassische Griechisch übersetzt.
In diesem Fall wäre es interessant, einmal zu schauen, ob wir Paulines und Pauls Formeln im Internet wiederfinden.