Einführung in die Automatentheorie/3. Stunde: Unterschied zwischen den Versionen
K (8 Versionen importiert) |
(formatiert) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 125: | Zeile 125: | ||
{{Fortsetzung|weiter=weiter mit der 4. Stunde|weiterlink=Einführung in die Automatentheorie/4.Stunde}} | |||
{{Einführung in die Automatentheorie}} | |||
Version vom 10. August 2019, 12:51 Uhr
Lösungen zu den beiden letzten Aufgaben aus der 2. Stunde
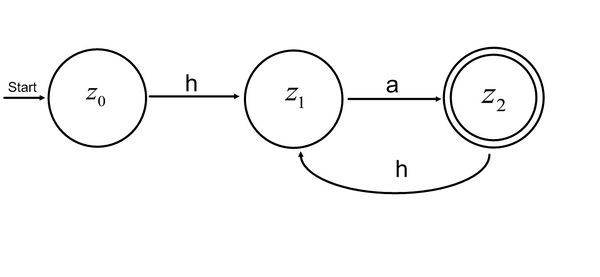
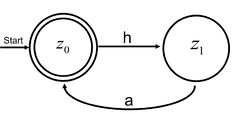
Aufgabe 2.5
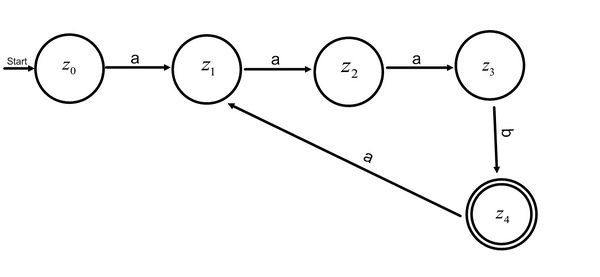
Aufgabe 2.6
Bei beiden Aufgaben darf der Startzustand nicht gleich dem Endzustand sein.
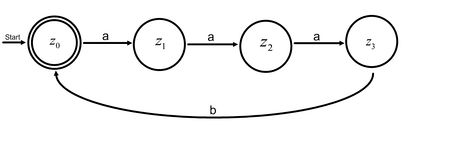
Überlege dir warum?
Akzeptanzverhalten
Die Aufgabe eines Automaten besteht oft darin, eine Eingabe auf Korrektheit zu überprüfen.
Eine Eingabe, bestehend aus einer Folge von Zeichen aus dem Eingabealphabet, wird genau dann von dem Automaten akzeptiert, wenn der Automat einen Endzustand erreicht.
So wird zum Beispiel bei Aufgabe 2.5 die Eingabe haha akzeptiert, aber hah nicht.
Die Automaten aus Aufgabe 2.5 und 2.6 gehören zu den endlich erkennenden Automaten.
Ein endlich erkennender Automat (Akzeptor) besteht aus den folgenden Bestandteilen:
- das Eingabealphabet E
- die endliche Menge der Zustände Z
- ein Startzustand
- mindestens einen Endzustand
- eine Übergangsfunktion f, die den Zeichen E und Zustand Z genau einen neuen Zustand zuordnet
Sprache des Automaten
Gelangt der Automat in den Akzeptierzustand, so bezeichnen wir die dazu notwendige Eingabefolge als ein Wort des Automaten. Die Menge aller akzeptierten Eingabefolgen, die man Wörter nennt, bezeichnen wir als Sprache des Automaten L.
Die Sprache eines Automaten L ist die Menge aller von ihm akzeptierten Wörter über dem Eingabealphabet E.
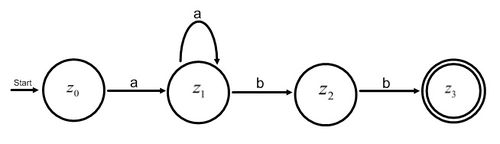
Schauen wir uns dazu nochmal die Aufgabe 2.5 an, bei der wir einen Automaten konstruieren sollten, der die Wörter ha, haha, hahaha usw. akzeptiert.
Die Aufgabe hätte auch so lauten können:
Konstruiere einen Automaten, der die Sprache L={(ha)n|n>0} akzeptiert.
Der Exponent n (also die Hochzahl) gibt die Anzahl der Folgen des Wortes ha an. Da in diesem Beispiel n>0 ist, muss das Wort ha mindestens einmal vorkommen.
Übungsaufgaben zu endlichen Automaten (Akzeptoren)
Hinweise:
- Ein Automat kann auch mehrere Endzustände besitzen.
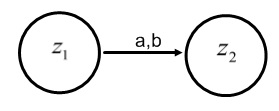
- Auf einer Übergangsfunktion können auch mehrere Zeichen vorhanden sein.
Der Zustand von z1 nach z2 erfolgt, wenn a oder b gelesen wird.
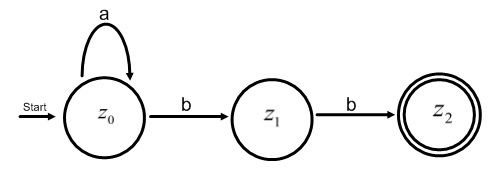
Konstruiere einen Akzeptor, der nur die folgende Sprache akzeptiert:
L={(anb2)}
Konstruiere einen Akzeptor, der nur die folgende Sprache akzeptiert:
L={(anb2)}
Konstruiere einen Akzeptor, der nur die folgende Sprache akzeptiert:
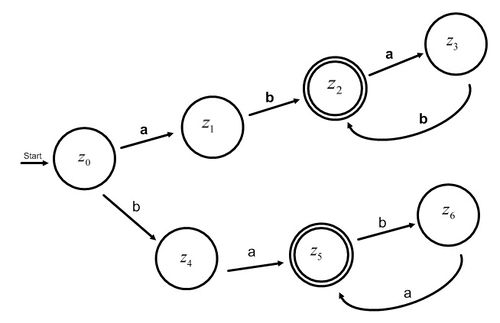
L={(ab)n} L={(ba)n}
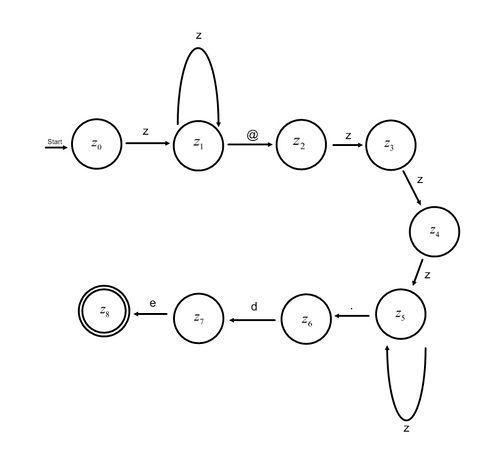
Konstruiere einen Akzeptor, der nur die folgenden Email-Adressen erkennt:
{min. ein Zeichen}@{mind. 3 Zeichen}.de
wobei ein Zeichen ein Element aus der Menge {a,...,z,A,...,Z,0,...9,+,-,_} sein soll.
Du kannst das Zeichen mit z bezeichnen, also z {a,...,z,A,...,Z,0,...9,+,-,_ }