Quadratische Funktionen erkunden/Übungen

Parameter

Scheitelpunktform

Übung

Für diese Übung benötigst du deinen Hefter (Lernpfadaufgaben, S. 16) .

In dieser Aufgabe werden die Parameter kombiniert, die du in dem Kapitel Die Parameter der Scheitelpunktform kennengelernt hast.

Gegeben ist die Wertetabelle:

a) Zeichne die Graphen zu den Funktionen f(x), g(x) und h(x) in das Koordinatensystem in deinem Hefter. Nicht alle y-Werte können sinnvoll in den Ausschnitt, der in dem Koordinatensystem gezeigt wird, eingetragen werden. <popup name="Lösung">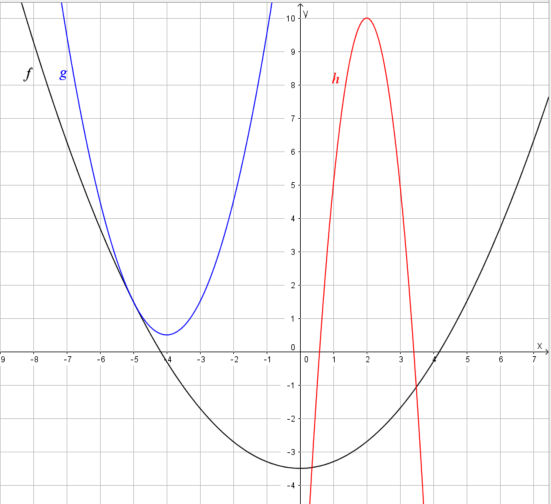</popup>

b) Bestimme die Funktionsterme in Scheitelpunktform.

<popup name="Hilfe">Lies zunächst den Scheitelpunkt ab und setze dessen Koordinaten an den passenden Stellen des allgemeinen Funktionsterms $f(x)=a(x-d)^2+e$ ein.

Ist der Graph gestreckt, gestaucht und/oder gespiegelt? Durch die Beantwortung dieser Frage kannst du den Wert des zugehörigen Parameters eingrenzen. Anschließend findest du den genauen Wert zum Beispiel durch systematisches Probieren und abgleichen mit den gegebenen Funktionswerten.</popup> <popup name="Lösung">$f(x)=1/5x^2-3.5$

$g(x)=(x+4)^2+0.5$

$h(x)=-5(x-2)^2+10$</popup>

Übung

{{{1}}}

Übung

{{{1}}}

Normalform

Übung

Übung

c) ablesen.

2. Verschiedene x-Werte in den Term einsetzen und so die zugehörigen y-Werte bestimmen (Erstellen einer Tabelle).

3. Koordinatensystem zeichnen und Punkte eintragen.

4. Punkte zu einer Parabel verbinden.</popup>

Allgemeine Übungen

Übung

Teste dein Wissen und werde Punkte-Millionär:

Übung

{{{1}}}

Von der Scheitelpunkt- zur Normalform

Übung

Quadratische Funktionen anwenden

Übung

- ! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter d !! Parameter e

Übung

{{{1}}}

Quadratische Funktionen erkunden

• Wiederholung
• Quadratische Funktionen im Alltag
• Quadratische Funktionen kennenlernen
• Die Parameter der Scheitelpunktform
• Die Scheitelpunktform
• Die Parameter der Normalform
• Die Normalform
• Von der Scheitelpunkt- zur Normalform
• Übungen

< Mathematik-digital

Erstellt von: Elena Jedtke (Diskussion)