Quadratische Funktionen erkunden/Von der Scheitelpunkt- zur Normalform: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Elena Jedtke
(Lösungsvorschlag Aufg 1)
Main>Elena Jedtke
KKeine Bearbeitungszusammenfassung
Zeile 75: Zeile 75:
{|
{|
|-
|-
|'''Funktionsterm Angry Birds'''||   '''Schritt-für-Schritt-Anleitung'''
|'''Funktionsterm Angry Birds'''||   '''Schritt-für-Schritt-Anleitung'''||   ||'''Funktionsterm Golden Gate Bridge'''||   '''Schritt-für-Schritt-Anleitung'''
|-
|-
|
|
|-
|-
|<math>f(x)=-0,13(x-7)^2+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
|<math>f(x)=-0,13(x-7)^2+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen||&nbsp;&nbsp;&nbsp;||<math>f(x)=0,04(x-5,7)^2+1</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
|-
|-
|
|
|-
|-
|<math>=-0,13((x-7)\cdot(x-7))+4,85</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|<math>=-0,13((x-7)\cdot(x-7))+4,85</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren||&nbsp;&nbsp;&nbsp;||<math>f(x)=0,04((x-5,7)(x-5,7))+1</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|-
|-
|
|
|-
|-
|<math>=-0,13(x^2-14x+49)+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|<math>=-0,13(x^2-14x+49)+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren||&nbsp;&nbsp;&nbsp;||<math>f(x)=0,04(x^2-11,4x+32,49)+1</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|
|
|-
|-
|<math>=-0,13x^2+1,82x-6,37+4,85</math>||&nbsp;&nbsp;&nbsp;Vereinfachen
|<math>=-0,13x^2+1,82x-6,37+4,85</math>||&nbsp;&nbsp;&nbsp;Vereinfachen||&nbsp;&nbsp;&nbsp;||<math>f(x)=0,04x^-0,456x+2,3</math>||&nbsp;&nbsp;&nbsp;Vereinfachen
|-
|-
|
|
|-
|-
|<math>=-0,13x^2+1,82x-1,52</math>
|<math>=-0,13x^2+1,82x-1,52</math>||&nbsp;&nbsp;&nbsp;||<math>f(x)=0,04(x-5,7)^2+1</math>
|}</popup>}}
|}</popup>}}


Version vom 20. Juli 2017, 08:59 Uhr

gRIFIKBERSCHREIBUNG)

Quadratische Funktionen erkunden

< Mathematik-digital


Bauarbeiter

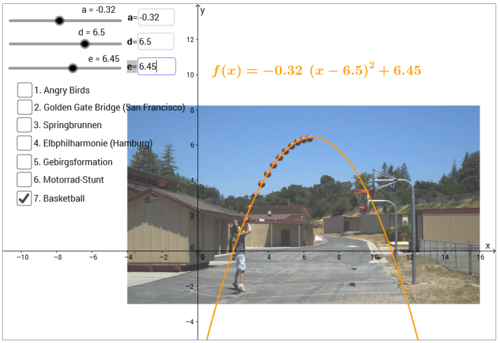
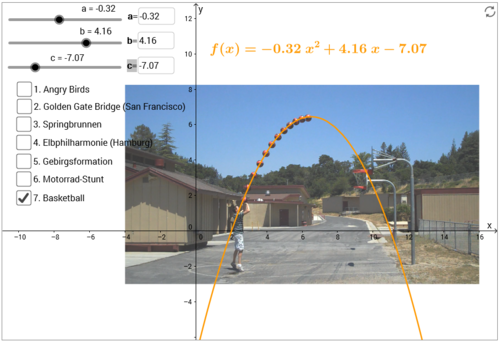
In diesem Kapitel kannst du herausfinden, wie du aus quadratischen Funktionen in Scheitelpunktform quadratische Funktionen in Normalform machen kannst.

Du lernst

1.

2.

3.


Nuvola apps edu miscellaneous.png   Beispiel

Für den Basketballwurf konnten näherungsweise diese beiden Funktionsterme gefunden werden:

Basketballwurf Parabel Basketballwurf Parabel

Die Funktionsterme müssen irgendwie ineinander überführbar sein, da sie die gleiche Parabel beschreiben.

Durch Ausmultiplikation der Scheitelpunktform erhalten wir:


Funktionsterm    Schritt-für-Schritt-Anleitung
   Klammer auflösen
   innere Klammer ausmultiplizieren
   Klammer ausmultiplizieren
   Vereinfachen


Ein Blick auf das zweite Bild oben zeigt, dass das Ergebnis der Ausmultiplikation genau der Term in Normalform ist.

Aufgabe 1




Pfeil Hier geht's weiter.png




Erstellt von: Elena Jedtke (Diskussion)

Abgerufen von „https://unterrichten.zum.de/index.php?title=Quadratische_Funktionen_erkunden/Von_der_Scheitelpunkt-_zur_Normalform&oldid=41641“