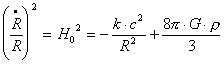Dunkle Materie

Welche Materie existiert im All?

Direkt sichtbar

• Nahe Planeten und Monde mit festen Oberflächen: Sie enthalten etwa gleichartige Elemente wie die Erde.
• Große gasförmige Planeten: Sie bestehen größtenteils aus Wasserstoff.
• Sonne und andere Sterne: Sie enthalten Wasserstoff und Helium und nur Spuren anderer Elemente.

Mit Hilfsmitteln registrierbar

• Staubwolken, die das Licht von Sternen abschirmen.
• Sterne, die in anderen Spektralbereichen leuchten.

Nicht registrierbar

Die Materie im Weltraum, die nicht beobachtet werden kann, da sie keine elektromagnetische Strahlung emittiert und auch keine sonst sichtbare Strahlung des Hintergrundes absorbiert, nennt man "Dunkle Materie". Auf ihre Existenz wird aus theoretischen Gründen geschlossen oder aus anderen Beobachtungen, die die Wirkung der Schwerkraft dieser Materie zeigen.

Einige Größen und Maße im Weltall

Längen	1 pc = 1 Parsec Entfernung, von der aus der Erdbahnradius unter einem Winkel von 1 Bogensekunde erscheint 1 Lj = 1 Lichtjahr Entfernung, die das Licht in einem Jahr zurücklegt 1 AE = 1 Astronomische Längeneinheit mittlerer Erdbahnradius
Umrechnungen	$1 pc \approx 3{,}26 Lj \approx 3{,}086 \cdot 10^{16} m$ $1 Lj \approx 9{,}5\cdot10^{15} m$ $1 AE \approx 1{,}5 \cdot 10^{11} m$
Massen	$1 SM = 1 M = 1 Sonnenmasse \approx 2 \cdot 10^{30} kg$

Milchstraße: ($10^{11}$ Sterne)

• sichtbarer Durchmesser 30-50 kpc (100-160 kLj)
• Dicke 0,5 kpc (1600 Lj) (am Kern ca 5 kpc)
• Masse $2 \cdot 10^{11}$ SM
• Sonne am Rand mit Abstand vom Zentrum 8,5 kpc (28 kLj)
• Entfernung zur Andromedagalaxie 700 kpc ($2{,}3 \cdot 10^6$ Lj)

Universum: ($10^{11}$ Galaxien)

• Durchmesser $6 \cdot 10^6$ kpc, ($2 \cdot 10^{10}$ Lj),

Was ist dunkle Materie?

Unter dem Begriff „Dunkle Materie“ versteht man die Materie im Weltraum, die nicht direkt beobachtet werden kann, da sie keine elektromagnetische Strahlung emittiert, die mit einem Teleskop auf der Erde empfangen wird, in keinem Spektralbereich, und die auch keine sonst sichtbare Strahlung des Hintergrundes absorbiert. Auf ihre Existenz wird aus Beobachtungen geschlossen, die die Wirkung der Schwerkraft zeigen, oder aus theoretischen Gründen.

Über die Menge der Dunklen Materie gibt es Vermutungen, die bis zum Hundertfachen der beobachtbaren Materie reichen. Man muss sich also das Universum mit einer großen Menge von unsichtbarer Materie gefüllt vorstellen, in die die sichtbaren Objekte als kleine leuchtende Punkte mit geringer Masse eingebettet sind.

Konsequenzen für die Theorie zur Entstehung und zur Entwicklung des Weltalls ergeben sich aus dieser großen Menge und aus der Unsicherheit über die wirkliche Menge. Aus den Beobachtungen von Hubble um 1930 wurde geschlossen, dass das Weltall sich ausdehnt. Gegen diese Fluchtbewegung wirkt die Masse durch die Gravitation bremsend. Ob diese Kraft aber ausreicht, die Fluchtbewegung so stark zu verlangsamen, dass sie nach endlicher Zeit zum Stillstand kommt und sich dann zu einer Kontraktion umwandelt, ist entscheidend für die Zukunft des Universums. Die Entscheidung ist durch die Abweichung der Materiedichte von der theoretisch ermittelten kritischen Dichte gegeben und abhängig von der Menge der insgesamt vorhandenen Masse und der noch genauer zu messenden Fluchtgeschwindigkeit.

Entdeckung und Messung der Dunklen Materie

1. Messung der Rotationskurven von Spiralgalaxien

Sichtbare Spiralgalaxien haben den überwiegenden Teil ihrer beobachtbaren Masse in einem begrenzten Bereich im Zentrum. Wenn man die Wirkung der Gravitationskraft dieser Masse auf kleine Massen weit außerhalb des Zentrums in den Spiralarmen kalkulieren möchte, kann man mit guter Näherung die Keplerbedingung(Beispiele für das Newtonsvhe Gravitationsgesetz) für unser Sonnensystem übernehmen, nach der sich die Geschwindigkeit umgekehrt proportional zur Wurzel aus dem Radius verhält. Für kleine Radien muss die Geschwindigkeit wegen der Wirkung der geringeren eingeschlossenen Masse kleiner sein.

Theoretische Geschwindigkeitsverteilung

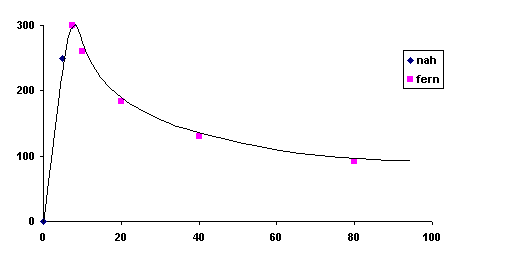(x-Achse: r in kpc, y-Achse: v(r) in km/s)

Theoretisch muss sich damit eine Geschwindigkeitsverteilung in Abhängigkeit vom Abstand (r) vom Zentrum in der Form ergeben, wie sie die Kurve andeutet. Für den ansteigenden Kurvenast wurde eine Proportionalität zu r und für den fallenden eine Proportionalität zu $1 / \sqrt{r}$ angesetzt. Die beiden Proportionalitätsfaktoren wurden so gewählt, dass die Skalierung der Achsen den Messverhältnissen entspricht und damit die Gesamtkurve mit den Messergebnissen leicht vergleichbar ist.

Experimentell werden die wirklichen Rotationsgeschwindigkeiten durch die Verschiebung von typischen Spektrallinien bekannter Elemente bestimmt. Dazu müssen die mittlere Fluchtgeschwindigkeit der gesamten Galaxie und die Geschwindigkeit des zu prüfenden kleinen Sterns relativ zur Erde durch die Dopplerverschiebung der Spektrallinien bestimmt werden. Die Sterne in den Spiralarmen auf verschiedenen Seiten zeigen auf der einen Seite eine stärkere, auf der anderen eine geringere Rotverschiebung als das Zentrum.

Durch Berücksichtigung der Bewegungsrichtung, die durch längere Beobachtungen und durch die Orientierung der Spiralarme bekannt ist, kann man die auf das Zentrum bezogenen Rotationsgeschwindigkeiten für Massen in verschiedenen Abständen vom Zentrum berechnen.

Gemessene Geschwindigkeitsverteilung der Spiralgalaxis NGC2885

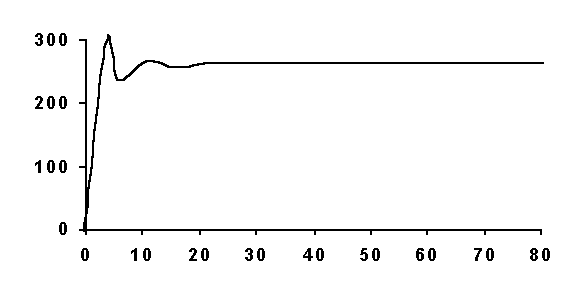(x-Achse: r in kpc, y-Achse: v(r) in km/s)

Aus den Messungen ergeben sich Kurven für die Geschwindigkeitsverteilungen, für die hier als typisches Beispiel die für die große Spiralgalaxie NGC2885 gezeigt ist.

2. Folgerung

Bei diesen hohen Geschwindigkeiten in großer Entfernung vom Zentrum können die Sterne nach den Keplerschen Gesetzen nicht mehr von der bekannten Zentralmasse gehalten werden. Da die Spiralgalaxien aber relativ stabile abgeschlossene Systeme sind, muss wesentlich mehr anziehende Masse vorhanden sein als beobachtbar ist, wenn man nicht die Gültigkeit des Gravitationsgesetzes in Frage stellen will. Die zusätzlich geforderte unsichtbare und unbekannte Materie nennt man „Dunkle Materie“.

Theoretisch kann man zeigen, dass sich bei großen Abständen eine konstante Geschwindigkeit ergibt, wenn man eine Massendichte postuliert, die umgekehrt proportional zum Quadrat des Abstandes vom Zentrum ist. Dazu ist eine räumlich ausgedehnte Massenverteilung erforderlich. Diese zusätzlich geforderte unsichtbare Masse um Spiralgalaxien könnte im Bereich des Halo liegen. Ihre Existenz wird zusätzlich auch für Theorien zur Beschreibung der Stabilität der Spiralgalaxien benötigt. Als Hinweise auf diese Materie können auch die in diesem Bereich sichtbaren Kugelsternhaufen, Zwerggalaxien und Sternwolken gedeutet werden. Sie haben aber nicht genügend viel sichtbare Materie für die geforderte Dichtefunktion und sind deshalb nur als Hinweis zu deuten.

Modellrechnungen müssen zunächst eine Dichtefunktion anpassen, die für kleine Radien etwa zu den beobachteten Massen passt, für Abstände von 5 kpc bis 10 kpc vom Zentrum aber in eine Funktion proportional zu 1 / r$^2$ übergeht. Weiterhin ist eine Abgrenzung zu großen Radien notwendig, da sich mit dieser Funktion durch Integration über die Kugelschalen eine proportional mit dem Radius wachsende Masse ergibt und damit keine Integration bis unendlich möglich ist. Wegen dieser unsicheren Grenzen liegt die Abschätzung der Menge des Anteils der dunklen Materie in Spiralgalaxien bei dem Faktor 4 bis 10,

d.h. die sichtbare Materie ist nur etwa 10 % bis 25 % der gesamten Masse.

3. Elliptische Galaxien und Galaxiengruppen

Elliptische Galaxien enthalten heiße Gase, die Röntgenstrahlung abgeben. Aus dem Spektrum und der Energieverteilung dieser Röntgenstrahlung kann man auf die Temperatur des Gases schließen, aus der sich die mittlere Geschwindigkeit und die Geschwindigkeitsverteilung ergibt. Die Geschwindigkeit der Gasteilchen und der sichtbaren Sterne ist so hoch, dass die Massen nicht durch die beobachtbare vorhandene Masse zusammengehalten werden können und deshalb die Galaxie verlassen müssten. Wegen der Stabilität der Galaxien muss aber gefordert werden, dass noch große Mengen an dunkler Materie in den Galaxien vorhanden sind, die die Materie binden.

Auch bei allen beobachteten Galaxiengruppen (Paare, Haufen, Superhaufen) ergeben die gemessenen Verteilungen der Geschwindigkeiten der einzelnen Galaxien, dass für die Stabilität dieser Gebilde eine wesentlich größere Masse erforderlich ist, als sie beobachtet werden kann. Wenn man für die sichtbaren Galaxien nach den oben beschriebenen Forderungen eine Massenkorrektur um den Faktor 4 bis 10 berücksichtigt, dann müssen die Galaxiensysteme etwa um einen weiteren Faktor 2 bis 5 mal mehr Masse enthalten, als sie durch die Summe der korrigierten einzelnen Massen gegeben ist.

Die für die Dynamik geforderte unsichtbare Masse wird auch dynamische Dunkle Materie genannt. Nach den beiden Korrekturen muss die gesamte Masse etwa um den Faktor 20 größer sein als die gesamte sichtbare Materie.

Kosmologische Gründe für die Existenz der Dunklen Materie

1. Dichteparameter

Der Dichteparameter Ω gibt die relative Massendichte des Universums bezüglich der kritischen Dichte an. Der Dichteparameter ist damit ein Maß für die Stabilität des gesamten Kosmos, denn für = 1 erhält man das stabile flache Universum, während für Ω> 1 das System kontrahieren, für Ω< 1 immer stärker expandieren muss. Da die Dichte der sichtbaren Materie mit etwa $2 \cdot 10^{-28}kg/m^3$ etwa um den Faktor 50 kleiner ist als die kritische Dichte, ergibt sich für sichtbare Materie der Dichteparameter $\Omega \approx 0{,}02$.

Schließt man in die Abschätzung des Dichtefaktors die dynamische dunkle Materie mit ein, dann wird die Dichte etwa um den Faktor 10 größer und der Dichtefaktor nähert sich mit $\Omega \approx 0{,}2$ schon besser dem idealen Wert 1; es wird aber immer noch eine Vergrößerung der Masse um einen weiteren Faktor 5 benötigt, wenn man den Wert 1 für das flache Universum als idealen Wert postuliert.

Da die kritische Dichte mit wachsendem Durchmesser sinkt, muss bei Ω > 1 der Dichtefaktor durch die Gravitation auch während der anfänglichen Expansion weiter wachsen und der Kosmos später einmal kontrahieren. Umgekehrt wird bei Ω < 1 der Kosmos immer stärker expandieren und damit Ω weiter sinken. Damit erzeugt jede Abweichung des Dichtefaktors von 1 im Laufe der Zeit eine Zunahme der Abweichung. Eine Abweichung um den Faktor 5 heute ist deshalb bezüglich der Zukunft wesentlich, nicht aber in Bezug auf die Entstehung des Universums, denn in einer Rückrechnung kann man bei den derzeitigen Modellen zeigen, dass diese große Abweichung zur Zeit t = 10$^{-33}$ Sekunden nach dem Urknall durch eine Abweichung um 10-50 von 1 bewirkt werden kann.

2. Standard-Urknallmodell

Das Standard-Urknallmodell eines flachen Universums basiert auf der Allgemeinen Relativitätstheorie von Einstein und fordert als Voraussetzung Homogenität und Isotropie im Weltraum. Eine wesentliche Voraussetzung ist die Annahme, dass die Massendichte gleich der kritischen Dichte ist. Damit muss der Dichteparameter die Größe = 1 haben, was mit den Beobachtungen nicht übereinstimmt.

Die Größe und vor Allem die Größenänderung des Universums werden durch den zeitabhängigen Skalenfaktor R(t) beschrieben. Für ihn gilt eine Potenzfunktion, nach der R(t) proportional zu t1/2 ist, wenn das Universum von Strahlung dominiert ist. Ist das Universum aber von Materie dominiert, dann ist der Skalenfaktor proportional zu t2/3 .

3. Änderungen nach dem Modell des Inflationären Universums

Im Modell des Inflationären Universums werden fast alle Regeln für das Standard-Urknallmodell übernommen, es wird lediglich eine kleine Korrektur für einen sehr kurzen Zeitraum in der Anfangsphase von 10-35 bis 10-33 Sekunden vorgenommen. Die Änderung soll eine anfangs wesentlich schnellere Ausdehnung beschreiben, als sie nach dem Standard-Urknallmodell erfolgt.

Auch dieses Modell basiert auf den Einsteinschen Feldgleichungen, die auch andere Lösungen haben können. Von de Sitter wurde gezeigt, dass sich auch eine exponentielle Ausdehnung in beschränkten Zeitintervallen ergeben kann, auch mehrfach und von unterschiedlichen skalaren Feldern ausgelöst.

Für die Größenvorstellung noch folgende Daten: Nach dem Standardmodell erreicht das Universum mit der Ausdehnung nach einer Potenzfunktion bis heute etwa R zcagleich.gif (178 Byte) 1030.RP , wobei RP der Skalenfaktor zur Planckzeit ist. Nach dem inflationären Modell erreicht das Universum in der kurzen Zeit bis t = 10-33 s nach einer Exponentialfunktion schon die Größe R zcagleich.gif (178 Byte) 10100.000.000·RP. Anschließend dehnt es sich langsamer weiter nach der Potenzfunktion aus, wie es im oberen Graphen gezeigt ist.

4. Zusammenfassung zur Menge der dunklen Materie

Die gesamte Masse, die nach dem inflationären Modell gefordert werden muss, ist etwa um den Faktor 5 größer als die, die aus dynamischen Beobachtungen erschlossen wird. Bezeichnet man die sichtbare Materie mit MS, dann ist die Masse der dynamischen dunklen Materie etwa 20 MS und die für die Modellrechnungen benötigte etwa 100 MS. Von der gesamten Materie im Universum ist also nur ein kleiner Teil von etwa 1% sichtbar.

Beobachtungen von Hubble

Messung: Aus der Rotverschiebung der Spektren des Sternlichtes lässt sich die Fluchtgeschwindigkeit berechnen, aus Helligkeit und Parallaxe erhält man die Entfernung der Sterne. Hubble hatte 1931 die Wertepaare aus Entfernung und Fluchtgeschwindigkeit für Sterne in Entfernungen bis etwa $10^8$ Lj gemessen.

Ergebnis: Die Fluchtgeschwindigkeit v ist proportional zur Entfernung r

Hubble-Konstante: $H_0 = v / r = (75 \pm 25) km/(s \cdot Mpc)$

Folgerung für Evolution: Durch Rückrechnung bei konstanter Geschwindigkeit v = H$_0$·r erhält man die Zeit t$_0$, die vergangen ist, seit das Universum die Größe Null hatte, zu

$t_0 = r / v = r / ( H_0 \cdot r ) = 1 / H_0 \approx 15 \cdot 10^9 a$ .

In der Literatur differieren die Werte im Bereich von 10·$10^9$ a bis 20·$10^9$ a je nach benutztem Wert der Hubble-Konstanten. Dabei wird vorausgesetzt, dass die Hubble-Konstante in der Zeit konstant geblieben ist. Bei einer Abnahme der Geschwindigkeit aufgrund der Gravitationskräfte kann die Zeit nur eine Obergrenze für das Weltalter sein.

Was ist die kritische Dichte?

Berechnung: Die kritische Dichte ist die Materiedichte im Weltall, bei der die Gravitationskräfte die Fluchtgeschwindigkeit gerade so stark abbremsen, dass sich die Geschwindigkeit dem Wert Null nähert, ohne ihn je zu erreichen. Nach der allgemeinen Relativitätstheorie ergibt sie sich zu

$\rho _C = \frac{3H_o^2}{8 \pi G} \approx 10^{-26}kg/m^3$.

Diese Dichte entspricht ca. 6 Protonen pro m3.

Dichteverteilung: Bei einer Abweichung der Dichte des Universums von der kritischen Dichte in Teilbereichen des Kosmos muss für diesen Bereich die Abweichung weiter zunehmen; denn geringe Dichte bewirkt Expansion und damit abnehmende Dichte und große Dichte bewirkt Abbremsen der Expansion und Übergang zur Kontraktion und damit zunehmende Dichte. Die in größeren Raumwinkelbereichen gemessene gleichmäßige Dichte kann deshalb nur erhalten geblieben sein, wenn zu Beginn die Dichte extrem gleichmäßig war. Dieser Zusammenhang wird mit dem Problem der Flachheit des Universums angesprochen.

Zur allgemeinen Relativitätstheorie

Vereinfachte Einsteinsche Feldgleichungen: $\mathbf{\Phi = 8 \pi G \rho + \Lambda}$

Die Potentiale werden durch das Produkt der Gravitationskonstante mit der mittleren Dichte dargestellt. Der Summand ist ein nachträglich eingeführter Abstoßungsterm, die so genannte „kosmologische Konstante“, mit der die Stabilität des Universums gesichert werden sollte. Sie wird im Standardmodell auf Null gesetzt.

Im homogenen Universum folgt aus den Feldgleichungen die Größe des Universums, der zeitabhängige Skalenfaktor R(t), der im geschlossen Universum dem Radius entspricht. Die relative Änderung des Skalenfaktors ist die Expansionsrate R'/R, die mit der Hubble-Konstanten H$_0$ identisch ist.

Für sie gilt:

Dabei ist k die Raumkrümmung, die direkt die weitere Evolution bestimmt.

Bedeutung der Raumkrümmung

Die Raumkrümmung wird durch den Faktor k in der Gleichung für die Expansionsrate beschrieben. Sie bestimmt direkt die weitere Evolution.

Für k = +1	erhält man ein geschlossenes Universum, das sich bis zu einer kritischen Größe ausdehnt und dann wieder zusammenzieht.
Für k = –1	erhält man ein offenes Universum, das sich immer weiter ausdehnt.
Für k = 0	erhält man den Grenzfall des flachen Universums, dessen Ausdehnungsgeschwindigkeit asymptotisch gegen Null geht.

Für das flache Universum kann man aus der Bedingung k = 0 die kritische Dichte berechnen, für die das Gleichgewicht zwischen Expansion und Kontraktion gehalten wird (s.o.).