Planetenbewegung
Wie bewegen sich die Planeten ?
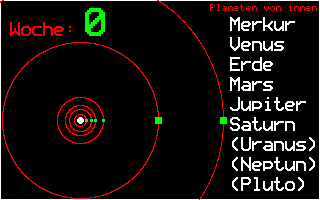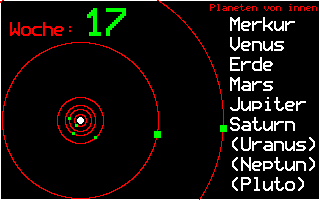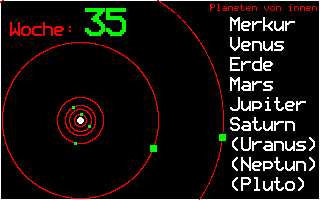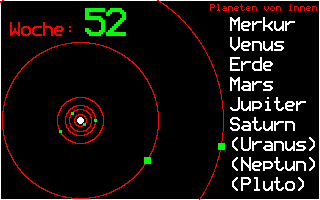
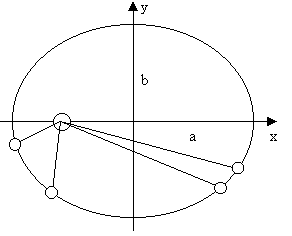
Nach Kepler bewegen sich die Planeten um die Sonne auf Ellipsenbahnen, die fast kreisförmig sind. Da die Planeten im Vakuum fliegen, müssen sie keine Reibungskräfte überwinden und benötigen deshalb keinen Antrieb; sie behalten die bei der Entstehung bekommene Anfangsgeschwindigkeit bei.
Das Bild zeigt die Bewegungen der 6 inneren Planeten für ein Jahr, wobei die Erde einen Umlauf um die Sonne macht.
Die Ellipsenbahn entsteht durch die Anziehung zur Sonne. Nach Newton fällt der Planet so schnell zur Sonne, dass er durch seine Trägheit und seine eigene Bahngeschwindigkeit gerade die Sonne nicht trifft, sondern immer um sie herumfällt. Je näher er der Sonne ist, um so schneller muss er sich bewegen, da die Anziehungskraft bei kleineren Abständen viel größer ist.
Keplersche Gesetze
Johannes Kepler (1571-1630)
Aus umfangreichem Beobachtungsmaterial von Tycho Brahe über die Bahnen der damals bekannten inneren 6 Planeten (vor allem Mars) ermittelte Kepler 3 Gesetze zur Beschreibung der Planetenbahnen.
Mit diesen Gesetzen werden die Bahnen der inneren 4 Planeten sehr gut beschrieben, aber bei Jupiter und Saturn waren Abweichungen erkennbar. Die Begründung für die Gesetze und die Abweichungen konnte erst durch Newton geliefert werden.
Newtonsche Gesetze
Isaac Newton (1643 - 1727)
Die Bewegungen aller Körper auf der Erde und im gesamten Kosmos werden durch drei Gesetze beschrieben
- Trägheitsprinzip: Jeder Körper verharrt in seinem Zustand der Ruhe oder der gleichförmigen geradlinigen Bewegung, solange keine äußeren Kräfte auf ihn einwirken.
- Grundgleichung der Mechanik: Die Änderung des Impulses (Produkt aus Masse und Geschwindigkeit) ist nach Richtung und Betrag gleich dem Produkt aus der Kraft und ihrer Einwirkungsdauer.
- Wechselwirkungsprinzip: Die Kräfte zweier Körper aufeinander sind stets von gleichem Betrag und entgegengesetzter Richtung.
Durch Anwendung dieser Gesetze auf die Bewegung der Planeten konnte Newton die Keplerschen Gesetze herleiten.
Für die gegenseitige Anziehungskraft F zwischen zwei Massen m und M im Abstand r ergibt sich das klassische Gravitationsgesetz
mit der Gravitationskonstanten .
Die Keplerschen Gesetze ergeben sich durch das Gleichgewicht aus Gravitationskraft und Trägheitskraft. Bei Ellipsenbahnen erhält man die Zunahme der Bahngeschwindigkeit durch die Beschleunigung bei Annäherung an die Sonne. Für die Beschreibung der Bewegung von Planeten oder Sternen, die um mehrere Massen innerhalb ihrer Bahn kreisen, muss man das allgemeinere Gravitationsgesetz nutzen.
Gravitationsgesetz von Isaac Newton
Eine kleine Masse m im Abstand r vom Zentrum einer großen Masse M bewegt sich mit der Geschwindigkeit v um das Zentrum. Die Geschwindigkeit ist abhängig vom Radius und von der Massenverteilung. Sie ist durch das Gleichgewicht aus der Zentrifugalkraft Z und der Gravitationskraft gegeben.
Die Gravitationskraft berechnet sich nach
wobei die Gravitationskonstante und M(r) die gesamte Masse innerhalb der Kugel mit Radius r um das Zentrum ist. Für Massen außerhalb von r heben sich im Mittel die Wirkungen auf die Masse m auf.
Mit erhält man durch Gleichsetzung für eine beliebige kleine Masse im Abstand r vom Zentrum eine Beziehung zwischen der eingeschlossenen Masse und der Bahngeschwindigkeit:
Aus der Bewegung von Planeten oder Sternen kann man über diese Formel auf die Verteilung der Massen innerhalb der Bahn schließen.
Beispiele für das Newtonsche Gravitationsgesetz
Für eine kleine Masse m auf Kreisbahnen mit Radius r um eine große Masse M innerhalb der Kugelschale gilt das Newtonsche Gravitationsgesetz
mit .
1. Anwendung in unserem Planetensystem für r>Sonnenradius, d.h. M(r)=konstant:
| v ~ 1 / |
|
- 2. Anwendung im starren Körper
- Dichte = konstant => M(r) ~ r3 => v ~ r d.h. keine Scherkräfte.
- 3. Anwendung für Bahngeschwindigkeiten unabhängig vom Radius
- v = konstant => M(r) ~ r ,
- mit ρ ~ M(r) / r3 => ρ ~ 1 / r2
Die drei Sonderfälle zeigen, dass aus der Geschwindigkeitsverteilung auf die Massenverteilung geschlossen werden kann. Das 3. Beispiel ist bei der Abschätzung zur Dunklen Materie wichtig.
Weblinks
Zu den Keplerschen Gesetzen findet man hier ein paar Animationen: