Grundlagen der Wahrscheinlichkeitsrechnung/Einführung in die Wahrscheinlichkeitsrechnung/Ergebnis und Ergebnismenge: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 103: | Zeile 103: | ||
| [[../Zufallsexperiment|Zurück zur letzten Seite]] || || || ||............. || || || || oder || || || ||............. || || || || [[../Ereignis|Weiter zur nächsten Seite]] | | [[../Zufallsexperiment|Zurück zur letzten Seite]] || || || ||............. || || || || oder || || || ||............. || || || || [[../Ereignis|Weiter zur nächsten Seite]] | ||
|} | |} | ||
{{Vorlage:Grundlagen der Wahrscheinlichkeitsrechnung}} | {{Vorlage:Grundlagen der Wahrscheinlichkeitsrechnung}} | ||
| Zeile 113: | Zeile 112: | ||
[[Kategorie:Sekundarstufe 1]] | [[Kategorie:Sekundarstufe 1]] | ||
[[Kategorie:ZUM2Edutags]] | [[Kategorie:ZUM2Edutags]] | ||
[[Kategorie:Interaktive Übung]] | |||
Version vom 8. September 2018, 07:43 Uhr
Zum Überlegen
Stelle dir vor, du spielst Mensch ärgere dich nicht und du benötigst eine 1 oder eine 2 beim Würfeln, um deine Figur ins Haus stellen zu können. Nun würfelst du. Notiere dir alle möglichen Ausgänge, die bei diesem Zufallsexperiment herauskommen können.
Ist es wahrscheinlicher, dass du deine Figur ins Haus stellen kannst oder dass es dir nicht gelingt? Begründe deine Antwort und tausche dich anschließend mit deiner Übungspartnerin/ mit deinem Übungspartner aus.
Was ist ein Ergebnis und eine Ergebnismenge?
Ihr wisst nach dem vorigen Abschnitt, was Zufallsexperiment sind. Zu jedem durchgeführten Zufallsexperiment gibt es ein Ergebnis und man kann eine Ergebnismenge, die alle möglichen Ergebnisse umfasst, angeben. Eine formale Definition von Ergebnis und Ergebnismenge lautet folgendermaßen:
Ein Ergebnis ist der (mögliche) Ausgang eines durchgeführten Zufallsexperiments.
Die Ergebnismenge fasst alle möglichen Ausgänge eines Zufallsexperiments zusammen.
Schreibweise:
Die Ergebnismenge Omega besteht aus den Ergebnissen 1,2 und 3.
Im obrigen Gedankenspiel solltet ihr die Ergebnismenge beim Würfeln bestimmen. Nun könnt ihr die Ergebnismenge mathematisch richtig aufschreiben! Da nur die AUgenzahlen 1 und 2 zum Erfolg führen und es mehr Augenzahlen gibt, die keinen Erfolg bringen, ist es eher unwahrscheinlich, dass man die Figur ins Haus stellen kann.
Beispiele für Ergebnisse und Ergebnismengen
Nun wollen wir uns auch hier konkrete Beispiele anschauen:
Bei der Shuffle-Funktion ist das Ergebnis der Song, der gerade gespielt wird.
- Die Ergebnismenge ist: {Goodbye Machine, Thoughts for the man, Beautiful heart, Summer of Lies, Turn up the Volume, I’m Insane, Get it together, Wicked madness, Bad lies, Hard chance}
Bei dem Münzwurf ist das Ergebnis, die Seite der Münze, die beim Durchgang oben liegt.
- Die Ergebnismenge bei einem Münzwurf ist: {Kopf, Zahl}
Aufgaben
Trage alle Ergebismengen für folgende Zufallsexperimente zusammen:
- a) Würfeln mit folgenden Würfeln:
- b) Man dreht folgende Glücksrader:
- c) Man würfelt zwei sechsseitige Würfel und addiert anschließend die Augensumme der Würfel.
a)Würfel mit acht Seiten: {1, 2, 3, 4, 5, 6, 7, 8}
Würfel mit 20 Seiten: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}
b):Das Glücksrad drehen:
- 1) {rot, blau, gelb, grün}
- 2) {rot, orange/Hauptgewinn, gelb, grün, hellblau, dunkelblau}
c):Die Augensumme bei einem Wurf mit zwei Würfeln: {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Beschreibe passende Zufallsexperimente für folgende Ergebnismengen:
- a) {Niete, kleiner Gewinn, mittlerer Gewinn, großer Gewinn}
- b) {Song 1, Song 2, Song 3, Song 4}
- c) {weiß, schwarz, rot, blau}
- d) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Achtung: Hierbei handelt es sich um eine beispielhafte Lösung! Eure eigenen Beispiele können und sollen ganz anders aussehen
- a): Man zieht aus einer Lostrommel, die Nieten, kleine, mittlere und große Gewinne enthält.
- b): Man drückt auf die zufällige Wiedergabe bei einer Playliste, die nur 4 Songs enthält.
- c): Man dreht ein Glücksrad, dass vier Sektoren enthält in den Farben weiß, schwarz, rot und blau.
- d): Man zieht aus einer Urne mit 10 Kugeln, die mit den Zahlen von 1 bis 10 beschriftet sind.
Im Folgenden siehst du verschiedene Würfel(-netze) und Glücksräder. Schreibe zu den gegeben Zufallsexperimenten die Ergebnismenge des jeweiligen Würfels/Glücksrad auf:
- a)

- 1) Zufallsexperiment: Man würfelt den Würfel einmal.
- 2) Zufalsexperiment: Man würfelt den Würfel zweimal und subtrahiert die kleinere Augenzahl von der größeren.
- b)
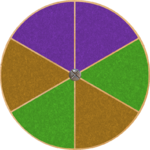
- 1) Zufallsexperiment: Man dreht das Glücksrad einmal
- 2) Zufallsexperiment: Man dreht das Glücksrad zweimal hintereinander und notiert die beiden Ergebnisse in der aufgetretenen Reihenfolge.
- c)
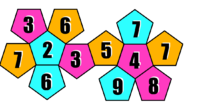
- 1) Zuafllsexperiment: Man würfelt den Würfel einmal und betrachtet die Farbe als Ergebnis.
- 2) Zufallsexperiment: Man würfelt und betrachtet die Augenzahl als Ergebnis.
Ergebnis zu a):
- 1) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
- 2) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
Ergebnis zu b):
- 1) {violett, grün, gelb}
- 2) {(violett,violett), (violett,grün), (violett,gelb), (grün,grün), (grün,violett),(grün,gelb), (gelb,gelb), (gelb,violett), (gelb,grün)}
Ergebnis zu c):
- 1) {pink, orange, hellblau}
- 2) {2, 3, 4, 5, 6, 7, 8, 9}
| Zurück zur letzten Seite | ............. | oder | ............. | Weiter zur nächsten Seite |
- Weißt du noch? Absolute und relative Häufigkeiten
- Einstiegsproblem: Die zufällige Shuffle-Funktion
- Simulation der Shuffle-Funktion
- Noch mehr Simulation zur Shuffle-Funktion
- Abschluss des Einstiegsproblems
- Einführung in die Wahrscheinlichkeitsrechnung








