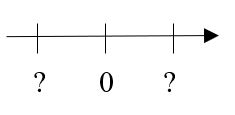Einführung in die Negativen Zahlen/Erweiterung der Zahlengeraden: Unterschied zwischen den Versionen
Main>Anto23 Keine Bearbeitungszusammenfassung |
Main>Anto23 Keine Bearbeitungszusammenfassung |
||
| Zeile 41: | Zeile 41: | ||
<nowiki>*</nowiki>f) -28 und 12<br> | <nowiki>*</nowiki>f) -28 und 12<br> | ||
<popup name="Tipp"> | <popup name="Tipp"> | ||
Die gesuchte Zahl muss zu beiden Zahlen denselben Abstand haben.<br>Wenn ihr nicht weiterkommt, nehmt | Die gesuchte Zahl muss zu beiden Zahlen denselben Abstand haben.<br>Wenn ihr nicht weiterkommt, nehmt die Zahlengerade zu Hilfe. | ||
</popup> | </popup> | ||
<br> | <br> | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
a) 12 | a) 12 b) -4 c) 2 d) 2 e) -68 f) -8 | ||
</popup> | </popup> | ||
|} | |} | ||
| Zeile 78: | Zeile 78: | ||
|} | |} | ||
<br> | <br> | ||
== Einzelnachweise == | |||
<references /> | <references /> | ||
Version vom 6. April 2018, 08:45 Uhr
|
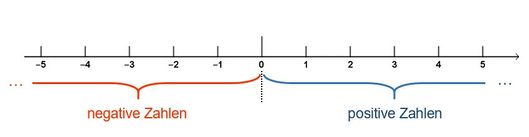
Frage
Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null?
|
|
|
|
|
<popup name="Lösungsvorschlag">
Links von der Null findet man die negativen Zahlen, rechts von der Null die positiven Zahlen. Die geschweiften Klammern haben jeweils drei Punkte, weil es unendlich viele positive und unendlich viele negative Zahlen gibt. Die gestrichelte Linie unter der 0 bedeutet, dass die 0 weder positiv noch negativ ist.</popup>
1. Findet zu jeder Situation eine passende ganze Zahl. Ordnet die Situation an die richtige Stelle auf der Zahlengeraden.
2. Von den beiden folgenden Aufgaben könnt ihr eine auswählen. Die linke Aufgabe ist etwas leichter als die rechte Aufgabe.
|
Welche Zahl liegt genau in der Mitte der angegebenen Zahlen?[2] |
Entgegengesetzte Zahlen und Betrag
Welche Zahlen könnt ihr für die Fragezeichen einsetzen? Löst und begründet eure Antwort auf dem Protokoll.
<popup name="Lösungsvorschlag"> Man kann für die Fragezeichen alle Zahlen einsetzen, die sich nur durch das Vorzeichen unterscheiden, also z.B. -3 & 3, -18 & 18, -5 & 5,… , da diese Zahlenpaare denselben Abstand zur 0 haben. </popup>
<popup name="Weitere Erklärungen zum Betrag">
Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Der Betrag ist immer positiv, hat also immer ein "+" als Vorzeichen, weil man ja nicht z.B. -9 Schritte gehen kann.</popup>