Quadratische Funktionen erkunden/Wiederholung (Optional): Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 8: Zeile 8:
{{Box|Aufgabe|
{{Box|Aufgabe|
Lücken-Mind Map oder Kreuzworträtsel - was machst du lieber? Suche dir eine der beiden folgenden Aufgaben aus und teste dein Wissen über (lineare) Funktionen.  Mit einem Klick in das weiße Kästchen oben rechts erhältst du den Vollbildmodus.
Lücken-Mind Map oder Kreuzworträtsel - was machst du lieber? Suche dir eine der beiden folgenden Aufgaben aus und teste dein Wissen über (lineare) Funktionen.  Mit einem Klick in das weiße Kästchen oben rechts erhältst du den Vollbildmodus.
{{Lösung versteckt|<iframe src="//LearningApps.org/watch?v=pbugpt1gt16" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|Kreuzworträtsel anzeigen|Kreuzworträtsel verbergen}}
{{Lösung versteckt|{{LearningApp|app=pbugpt1gt16|width:100%|height:500px}}|Kreuzworträtsel anzeigen|Kreuzworträtsel verbergen}}


<popup name="Lücken-Mind Map"><iframe src="//LearningApps.org/watch?v=pp5okr7zk16" style="border:0px;width:100%;height:500px;center" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe></popup>|Arbeitsmethode}}
{{Lösung versteckt|{{LearningApp|app=pp5okr7zk16|width:100%|height:500px}}|Lücken-Mindmap anzeigen|Lücken-Mindmap verbergen}}
|3=Arbeitsmethode}}




Zeile 20: Zeile 21:
'''a)''' Beantworte die Frage in dem Applet. ''Hinweis'': Es gibt genau eine richtige Antwort.
'''a)''' Beantworte die Frage in dem Applet. ''Hinweis'': Es gibt genau eine richtige Antwort.


<iframe src="//LearningApps.org/watch?v=p563afae517" style="border:0px;width:80%;height:500px" webkitallowfullscreen="false" mozallowfullscreen="true"></iframe>
{{LearningApps|app=p563afae517|width:100%|height:500px}}


'''b)''' Überlege dir eine Begründung für die richtige Darstellung der Entfernung zum Startpunkt.
'''b)''' Überlege dir eine Begründung für die richtige Darstellung der Entfernung zum Startpunkt.
Zeile 36: Zeile 37:
{{Box|Aufgabe|
{{Box|Aufgabe|


<iframe src="//LearningApps.org/watch?v=pohhfm2vj16" style="border:0px;width:80%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe>|Arbeitsmethode}}
{{LearningApps|app=pohhfm2vj16|width:100%|height:500px}}
|3=Arbeitsmethode}}




Version vom 24. Februar 2018, 15:55 Uhr

gRIFIKBERSCHREIBUNG)

Quadratische Funktionen erkunden

< Mathematik-digital


Hinweis
Bevor du loslegst, dich in das neue Thema Quadratische Funktionen einzuarbeiten, kannst du auf dieser Seite dein bisheriges Wissen über Funktionen auffrischen.


Teste dein Wissen über (lineare) Funktionen

Aufgabe

Lücken-Mind Map oder Kreuzworträtsel - was machst du lieber? Suche dir eine der beiden folgenden Aufgaben aus und teste dein Wissen über (lineare) Funktionen. Mit einem Klick in das weiße Kästchen oben rechts erhältst du den Vollbildmodus.


Graphen zu einer Sachsituation

Aufgabe

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 1) Notizblock mit Bleistift.

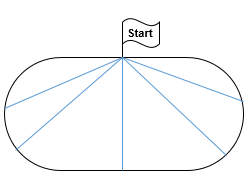
a) Beantworte die Frage in dem Applet. Hinweis: Es gibt genau eine richtige Antwort.

Vorlage:LearningApps

b) Überlege dir eine Begründung für die richtige Darstellung der Entfernung zum Startpunkt.

<popup name="Hilfe">Zeichne eine Skizze der Laufbahn in deinen Hefter und trage für ein paar Punkte auf der Bahn die Luftlinien zum Startpunkt ein. Wo ist der Abstand am größten? Wo ist er am geringsten?</popup> <popup name="Lösung">Der Graph beginnt im Ursprung des Koordinatensystems. Da Start und Ziel identisch sind, endet der Graph auf der x-Achse. Sein Verlauf lässt sich durch die Bewegung der Läufer beschreiben:

Sportfest

Zunächst bewegen sich die Läufer von dem Startpunkt weg. In der zweiten Kurve wird ihr Abstand (Luftlinie) zum Start wieder geringer, bis sie genau gegenüber vorbeilaufen. Ab diesem Punkt steigt der Abstand (Luftlinie) noch einmal an und nähert sich schließlich ab der dritten Kurve wieder dem Startpunkt an.</popup>


Zeigt der Graph einen funktionalen Zusammenhang?

Aufgabe


Vorlage:LearningApps


Videos und Merksätze

Daniel Jung hat auf Youtube in seinem Channel Mathe by Daniel Jung zu den verschiedensten Themen Erklärvideos erstellt. Hier kannst du dir Videos zu dem Thema Was ist eine Funktion? bzw. eine Übersicht über Lineare Funktionen anschauen. Denke daran dir Kopfhörer anzuziehen, sofern du nicht alleine in einem Raum bist.


Merke


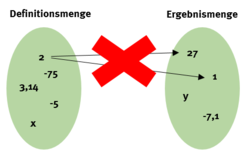
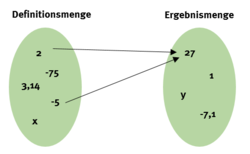
  • Eine Funktion ordnet jedem Element einer Ausgangsmenge (Definitionsmenge) genau ein Element der Zielmenge (Ergebnismenge) zu. Ein Element aus der Ergebnismenge kann mehreren Elementen der Definitionsmenge zugeordnet werden.

Kein fkt. Zsmh. Fkt. Zsmh.

  • Lineare Funktionen liegen in der Form vor, wobei m die Steigung der Geraden und b den y-Achsenabschnitt angibt.
  • Funktionen mit dem Term nennt man proportionale Funktionen. Sie sind ein Spezialfall der linearen Funktionen.


Pfeil Hier geht's weiter.png


Erstellt von: Elena Jedtke (Diskussion)

Abgerufen von „https://unterrichten.zum.de/index.php?title=Quadratische_Funktionen_erkunden/Wiederholung_(Optional)&oldid=42194“