Quadratische Funktionen erkunden/Von der Scheitelpunkt- zur Normalform: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Main>Elena Jedtke
(Aufgabe 1 neu)
Main>Elena Jedtke
(Lösungsvorschlag Aufg 1)
Zeile 72: Zeile 72:


<popup name="Hinweis">Es kann sein, dass dein Ergebnis etwas von deinem eigenem Normalformterm abweicht. Das liegt dann daran, dass du die Parabel bei der Aufgabe auf der Normalformseite nicht genau gleich in das Bild gelegt hast wie auf der Scheitelpunktseite. Du solltest dich jedoch in dem angegebenen Spielraumbereich der Lösungsvorschläge befinden.</popup>
<popup name="Hinweis">Es kann sein, dass dein Ergebnis etwas von deinem eigenem Normalformterm abweicht. Das liegt dann daran, dass du die Parabel bei der Aufgabe auf der Normalformseite nicht genau gleich in das Bild gelegt hast wie auf der Scheitelpunktseite. Du solltest dich jedoch in dem angegebenen Spielraumbereich der Lösungsvorschläge befinden.</popup>
<popup name="Lösung">folgt</popup>}}
<popup name="Lösungsvorschläge">
{|
|-
|'''Funktionsterm Angry Birds'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''
|-
|
|-
|<math>f(x)=-0,13(x-7)^2+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
|-
|
|-
|<math>=-0,13((x-7)\cdot(x-7))+4,85</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|-
|
|-
|<math>=-0,13(x^2-14x+49)+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|
|-
|<math>=-0,13x^2+1,82x-6,37+4,85</math>||&nbsp;&nbsp;&nbsp;Vereinfachen
|-
|
|-
|<math>=-0,13x^2+1,82x-1,52</math>
|}</popup>}}




Version vom 20. Juli 2017, 08:57 Uhr

gRIFIKBERSCHREIBUNG)

Quadratische Funktionen erkunden

< Mathematik-digital


Bauarbeiter

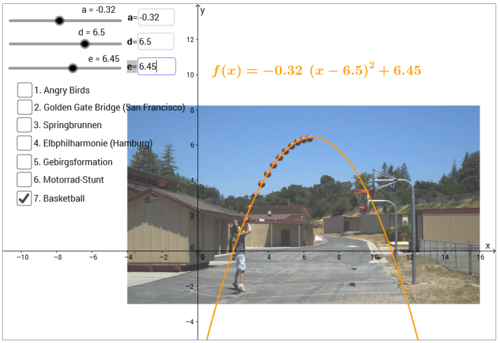
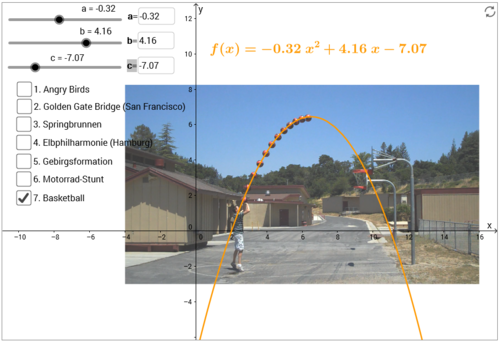
In diesem Kapitel kannst du herausfinden, wie du aus quadratischen Funktionen in Scheitelpunktform quadratische Funktionen in Normalform machen kannst.

Du lernst

1.

2.

3.


Nuvola apps edu miscellaneous.png   Beispiel

Für den Basketballwurf konnten näherungsweise diese beiden Funktionsterme gefunden werden:

Basketballwurf Parabel Basketballwurf Parabel

Die Funktionsterme müssen irgendwie ineinander überführbar sein, da sie die gleiche Parabel beschreiben.

Durch Ausmultiplikation der Scheitelpunktform erhalten wir:


Funktionsterm    Schritt-für-Schritt-Anleitung
   Klammer auflösen
   innere Klammer ausmultiplizieren
   Klammer ausmultiplizieren
   Vereinfachen


Ein Blick auf das zweite Bild oben zeigt, dass das Ergebnis der Ausmultiplikation genau der Term in Normalform ist.

Aufgabe 1




Pfeil Hier geht's weiter.png




Erstellt von: Elena Jedtke (Diskussion)

Abgerufen von „https://unterrichten.zum.de/index.php?title=Quadratische_Funktionen_erkunden/Von_der_Scheitelpunkt-_zur_Normalform&oldid=41640“