Signifikanztest für binomialverteilte Zufallsgrößen/Fehlerarten beim Signifikanztest: Unterschied zwischen den Versionen
K (Rechtschreibfehler verbessert) Markierung: Quelltext-Bearbeitung 2017 |
K (Rechtschreibfehler verbessert) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 1: | Zeile 1: | ||
In den Klausuraufgaben wird von euch manchmal gefordert die Fehlerarten die bei einem Signifikanztest auftreten können zu beschreiben. In folgendem Abschnitt soll dies nochmals kurz wiederholt werden und euch praktische Hinweise gegeben werden, wie ihr diese für die Klausuraufgaben beschreiben könnt.<br><br> | In den Klausuraufgaben wird von euch manchmal gefordert, die Fehlerarten, die bei einem Signifikanztest auftreten können, zu beschreiben. In folgendem Abschnitt soll dies nochmals kurz wiederholt werden und euch praktische Hinweise gegeben werden, wie ihr diese für die Klausuraufgaben beschreiben könnt.<br><br> | ||
Folgende Fehlerarten können beim Signifikanztest auftreten:<br><br> | Folgende Fehlerarten können beim Signifikanztest auftreten:<br><br> | ||
| Zeile 7: | Zeile 7: | ||
|3=Merksatz}} | |3=Merksatz}} | ||
Anmerkung: | Anmerkung: Der Fehler 1. und 2. Art kann nur berechnet werden, wenn die tatsächliche Verteilung (also p) bekannt ist. Da dies eigentlich nie der Fall ist, ist die Diskussion etwas theoretisch. | ||
Zur Veranschaulichung der beiden | Zur Veranschaulichung der beiden Fehlerarten betrachten wir wieder unser Beispiel: <br><br> | ||
Die Umweltgruppe will zeigen, dass durch die Fridays For Future Demos der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung sehen, im Vergleich zu 2019 (2019 lag der Wert bei 71%) gestiegen ist. Sie wählen die Hypothesen wie folgt: | Die Umweltgruppe will zeigen, dass durch die Fridays For Future Demos der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung sehen, im Vergleich zu 2019 (2019 lag der Wert bei 71%) gestiegen ist. Sie wählen die Hypothesen wie folgt: | ||
<math>H_0:p\leq0,71</math> und <math>H_1:p>0,71</math><br> | <math>H_0:p\leq0,71</math> und <math>H_1:p>0,71</math><br> | ||
| Zeile 16: | Zeile 16: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
<u>Fehler 1. Art:</u> Der tatsächliche Anteil, der Menschen die den Klimawandel als Bedrohung sehen, beträgt ''' | <u>Fehler 1. Art:</u> Der tatsächliche Anteil, der Menschen die den Klimawandel als Bedrohung sehen, beträgt '''höchstens''' 71%, durch den Test wird aber fälschlicherweise angenommen, dass der Anteil '''gestiegen''' ist. <br> | ||
<u>Fehler 2. Art: </u>Der tatsächliche Anteil liegt''' über''' 71% (in dem Fall bei 76%), der Test erkennt dies aber nicht. Das heißt der Test verwirft fälschlicherweise die Nullhypothese '''nicht'''. | <u>Fehler 2. Art: </u>Der tatsächliche Anteil liegt''' über''' 71% (in dem Fall bei 76%), der Test erkennt dies aber nicht. Das heißt der Test verwirft fälschlicherweise die Nullhypothese '''nicht'''. | ||
</div> | </div> | ||
| Zeile 26: | Zeile 26: | ||
{{Box|1=Übung 1: Fehlerarten bestimmen|2= | {{Box|1=Übung 1: Fehlerarten bestimmen|2= | ||
Die Partei, die den Klimawandel nicht als Bedrohung sieht, hofft | Die Partei, die den Klimawandel nicht als Bedrohung sieht, hofft, dass ihre Argumente im letzten Jahr gegen die Bedrohung des Klimawandels bei der Bevölkerung angekommen sind. Die Partei interessiert sich, ob dadurch der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung ansehen im Vergleich zur 2019 (2019 lag der Wert bei 71%) gesunken ist. Sie testen mit folgenden Hypothesen: | ||
<br><math>H_0:p\geq0,71</math> und <math>H_1:p<0,71</math><br><br> | <br><math>H_0:p\geq0,71</math> und <math>H_1:p<0,71</math><br><br> | ||
Beschreibe in Worten, worin der Fehler 1. Art im Kausalzusammenhang besteht. | Beschreibe in Worten, worin der Fehler 1. Art im Kausalzusammenhang besteht. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Fehler 1. Art besteht | Der Fehler 1. Art besteht darin, dass mindestens 71% der Menschen den Klimawandel als Bedrohung ansehen, durch den Test aber aber vermutet wird, dass der Anteil gesunken ist. | ||
}} | }} | ||
Beschreibe in Worten, worin der Fehler 2. Art im Kausalzusammenhang besteht. | Beschreibe in Worten, worin der Fehler 2. Art im Kausalzusammenhang besteht. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Der Fehler 2. Art besteht | Der Fehler 2. Art besteht darin, dass tatsächlich weniger als 71% der Menschen in Deutschland den Klimawandel als Bedrohung ansehen, der Test dies aber nicht erkennt. Das heißt der Test verwirft fälschlicherweise die Nullhypothese nicht. | ||
}} | }} | ||
Version vom 12. Januar 2020, 10:55 Uhr
In den Klausuraufgaben wird von euch manchmal gefordert, die Fehlerarten, die bei einem Signifikanztest auftreten können, zu beschreiben. In folgendem Abschnitt soll dies nochmals kurz wiederholt werden und euch praktische Hinweise gegeben werden, wie ihr diese für die Klausuraufgaben beschreiben könnt.
Folgende Fehlerarten können beim Signifikanztest auftreten:
Der Fehler 1. Art wird oft auch als -Fehler bezeichnet. Diesen Fehler habt ihr bereits kennengelernt. Beim Fehler 1. Art wird eine Nullhypothese fälschlicherweise verworfen. Dieser Fehler wird durch das festgelegte Signifikanzniveau kontrolliert. Die Wahrscheinlichkeit für den Fehler 1. Art kann also nie größer als das festgelegte Signifkanzniveau sein.
Anmerkung: Der Fehler 1. und 2. Art kann nur berechnet werden, wenn die tatsächliche Verteilung (also p) bekannt ist. Da dies eigentlich nie der Fall ist, ist die Diskussion etwas theoretisch.
Zur Veranschaulichung der beiden Fehlerarten betrachten wir wieder unser Beispiel:
Die Umweltgruppe will zeigen, dass durch die Fridays For Future Demos der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung sehen, im Vergleich zu 2019 (2019 lag der Wert bei 71%) gestiegen ist. Sie wählen die Hypothesen wie folgt:
und
Der tatsächliche Wert, den die Gruppe natürlich nicht weiß, liegt im Jahr 2020 bei 76%. (Hinweis: Es ist ein fiktiver Wert)
Welche Fehler können der Gruppe beim Testen unterlaufen?
Fehler 1. Art: Der tatsächliche Anteil, der Menschen die den Klimawandel als Bedrohung sehen, beträgt höchstens 71%, durch den Test wird aber fälschlicherweise angenommen, dass der Anteil gestiegen ist.
Fehler 2. Art: Der tatsächliche Anteil liegt über 71% (in dem Fall bei 76%), der Test erkennt dies aber nicht. Das heißt der Test verwirft fälschlicherweise die Nullhypothese nicht.
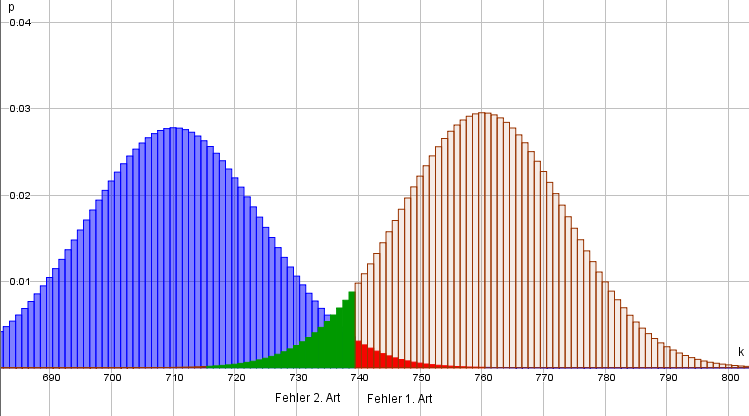
Die Grafik veranschaulicht beide Fehlerarten.
Der blaue Graph ist der Grenzfall der Nullhypothese und der rote Graph ist die Verteilung, mit der für die Gruppe unbekannten Wahrscheinlichkeit von 2020. Der Fehler 1. Art ist rot markiert und der Fehler 2. Art grün.
Die Partei, die den Klimawandel nicht als Bedrohung sieht, hofft, dass ihre Argumente im letzten Jahr gegen die Bedrohung des Klimawandels bei der Bevölkerung angekommen sind. Die Partei interessiert sich, ob dadurch der Anteil der Menschen in Deutschland, die den Klimawandel als Bedrohung ansehen im Vergleich zur 2019 (2019 lag der Wert bei 71%) gesunken ist. Sie testen mit folgenden Hypothesen:
und
Beschreibe in Worten, worin der Fehler 1. Art im Kausalzusammenhang besteht.
Beschreibe in Worten, worin der Fehler 2. Art im Kausalzusammenhang besteht.



