Main>Leonie Porzelt |
|
| (43 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| __NOTOC__ | | __NOTOC__ |
| {{Lernpfad-M| | | {{Box|1=Abbildung durch zentrische Streckung|2= |
| ===Abbildung durch zentrische Streckung===
| | [[Bild:Porzelt_Zentrische_Streckung.jpg|right|250px]] |
| }}
| | In diesem Lernpfad durchläufst du 6 Stationen. |
| <br>
| | Unten siehst du alle Stationen in einer Übersicht. |
| [[Bild:Porzelt_Zentrische_Streckung.jpg|center]] | | Die 6. Station ist eine Station für Profis mit extra Informationen.|3=Lernpfad}} |
| <br>
| | |
| | |
| | {{Abbildungen durch zentrische Streckung}} |
| | |
| | |
| ==1. Station: Ähnlichkeitsabbildung== | | ==1. Station: Ähnlichkeitsabbildung== |
| :Hier siehst du Panto mit einer Taschenlampe. Schalte die Taschenlampe ein, dann leuchtet
| |
| :sie direkt auf einen grünen Strohhalm. An der Wand entsteht dabei ein Schatten.
| |
| :Verschiebe Panto näher an den Strohhalm heran, oder weiter von dem Strohhalm weg.
| |
| <br>
| |
| <br>
| |
| <ggb_applet height="500" width="800" showResetIcon="true" filename="Porzelt_Taschenlampe.ggb" />
| |
| <br>
| |
| <br>
| |
| <br>
| |
| :'''''Lies die folgenden Beobachtungen konzentriert durch und hake die richtigen Aussagen ab:'''''
| |
|
| |
|
| <br> | | Hier siehst du Panto mit einer Taschenlampe. Schalte die Taschenlampe ein, dann beleuchtet |
| | sie direkt einen grünen Strohhalm. An der Wand entsteht dabei ein Schatten. |
| | Schiebe Panto näher an den Strohhalm heran und dann weiter von dem Strohhalm weg! |
| | |
| | <ggb_applet height="500" width="800" showResetIcon="true" id="eamfm2tn" /> |
| | |
| | '''Lies die folgenden Beobachtungen konzentriert durch und setze einen Hacken bei den richtigen Aussagen:''' |
| <div class="multiplechoice-quiz"> | | <div class="multiplechoice-quiz"> |
|
| |
| '''Wie ändert sich der Schatten durch das Verschieben?''' | | '''Wie ändert sich der Schatten durch das Verschieben?''' |
| (Je '''näher''' Panto mit der Taschenlampe auf den Strohhalm leuchtet, desto '''größer''' ist der Schatten.) | | (Je '''näher''' Panto mit der Taschenlampe auf den Strohhalm leuchtet, desto '''größer''' ist der Schatten.) |
| Zeile 26: |
Zeile 25: |
| (Je '''weiter''' Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto '''kleiner''' ist der Schatten.) | | (Je '''weiter''' Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto '''kleiner''' ist der Schatten.) |
| (!Je '''weiter''' Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto '''größer''' ist der Schatten.) | | (!Je '''weiter''' Panto mit der Taschenlampe von dem Strohhalm entfernt ist, desto '''größer''' ist der Schatten.) |
|
| |
| </div> | | </div> |
|
| |
|
| <br>
| | :'''''Den folgenden Text musst du genau durchlesen, denn am Ende wirst du darüber abgefragt.''''' |
| :Lies den Text genau durch. Am Ende wirst du darüber abgefragt. | | [[Bild:Porzelt_Panto-1.jpg|right]] |
| <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;">
| | {{Box|1=Merke|2= |
| :Der Strohhalm wird als '''Urbild''' und der Schatten als '''Bild''' bezeichnet. | | :Der Strohhalm wird als '''Urbild''' und der Schatten als '''Bild''' bezeichnet. |
| :Wie man sieht haben der Strohhalm und der Schatten verschiedene Größen, doch sie sind sich ähnlich. | | :Wie man sieht, unterscheiden sich der Strohhalm und der Schatten nur in ihrer Größe aber nicht in ihrer Form. |
| :Deshalb spricht man von einer '''Ähnlichkeitsabbildung'''.
| | :Sie sind sich ähnlich. Deshalb spricht man hier von einer '''Ähnlichkeitsabbildung'''. |
| :Die Vergrößerung geht von einem Zentrum, in unserem Beispiel der Taschenlampe, aus. Man spricht hierbei von | | :Die Vergrößerung geht von einem Zentrum, in unserem Beispiel der Taschenlampe, aus. Man spricht hierbei von |
| :einer '''zentrischen Streckung'''. Das '''Streckungszentrum''' wird mit '''Z''' bezeichnet. | | :einer '''zentrischen Streckung'''. Das '''Streckungszentrum''' wird mit '''Z''' bezeichnet. |
| :Urbild, Bild und Streckungszentrum liegen auf den Lichtstrahlen, die von der Taschenlampe ausgehen. Diese | | :Urbild, Bild und Streckungszentrum liegen auf den Lichtstrahlen, die von der Taschenlampe ausgehen. Diese |
| :Lichtstrahlen sind '''Halbgeraden'''. | | :Lichtstrahlen sind '''Halbgeraden'''.|3=Merksatz}} |
| </div>
| |
| <br>
| |
| :[[/Hier kannst du weitere Beispiele einer zentrischen Streckung sehen/]]
| |
| <br>
| |
| | |
| ==2. Station: Streckungsfaktor==
| |
| :In dem nächsten Fall ist das Urbild ein Dreieck, dass du zentrisch strecken kannst, indem du an dem Schieberegler ziehst.
| |
| :Der Schieberegler durchläuft die positiven Zahlen von k=0 bis k=3.
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| {| <br>
| |
| |<ggb_applet height="320" width="700" showResetIcon="true" filename="Porzelt_positiverStreckungsfaktor.ggb" />||'''Was verändert sich? Orientiere dich dabei an diesen Fragen:'''
| |
| <quiz display="simple">
| |
| | |
| {'''Auf welcher Seite von Z liegen das Urbild und das Bild?'''}
| |
| +auf derselben Seite
| |
| -auf verschiedenen Seiten
| |
| | |
| {'''Was liegt bei k>1 vor?'''}
| |
| +eine Vergrößerung
| |
| -eine Verkleinerung
| |
| -die Identität
| |
| | |
| {'''Was liegt bei 0<k<1 vor?'''}
| |
| -eine Vergrößerung
| |
| +eine Verkleinerung
| |
| -die Identität
| |
| | |
| {'''Was liegt bei k=1 vor?'''}
| |
| -eine Vergrößerung
| |
| -eine Verkleinerung
| |
| +die Identität
| |
| | |
| {'''Was passiert wenn k=0 ist?'''}
| |
| +es erfolgt '''keine''' zentrische Streckung
| |
| -es erfolgt '''eine''' zentrische Streckung
| |
| | |
| </quiz>
| |
| |}
| |
| </div>
| |
| <br>
| |
| | |
| <br>
| |
| :Was sind die Unterschiede, wenn du dieses Dreieck zentrisch streckst? Dieses mal durchläuft der
| |
| :Schieberegler die negativen Zahlen von k=-3 bis k=0.
| |
| <br>
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| {| <br>
| |
| |<ggb_applet height="400" width="750" showResetIcon="true" filename="Porzelt_negativerStreckungsfaktor.ggb" />||'''Was verändert sich? Orientiere dich dabei an diesen Fragen:'''
| |
| <quiz display="simple">
| |
| | |
| {'''Auf welcher Seite von Z liegen das Urbild und das Bild?'''}
| |
| -auf derselben Seite
| |
| +auf verschiedenen Seiten
| |
| | |
| {'''Was liegt bei k< -1 vor?'''}
| |
| +eine Vergrößerung
| |
| -eine Verkleinerung
| |
| -die Identität
| |
| -eine Spiegelung
| |
| | |
| {'''Was liegt bei 0>k> -1 vor?'''}
| |
| -eine Vergrößerung
| |
| +eine Verkleinerung
| |
| -die Identität
| |
| -eine Spiegelun)
| |
| | |
| {'''Was liegt bei k= -1 vor?'''}
| |
| -eine Vergrößerung
| |
| -eine Verkleinerung
| |
| -die Identität
| |
| +eine Spiegelung
| |
|
| |
|
| </quiz>
| |
| |}
| |
| </div>
| |
| <br>
| |
| <br>
| |
| :Um herauszufinden was das k bedeutet, musst du dir jetzt bei dieser zentrischen Streckung anschauen, wie
| |
| :sich die Streckenlängen verändern, wenn du k veränderst. Dazu musst du dir die Streckenlängen anzeigen lassen.
| |
| <br>
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| {| <br>
| |
| |<ggb_applet height="400" width="850" showResetIcon="true" filename="Porzelt_Streckungsfaktor.ggb" />||'''Was verändert sich? Orientiere dich dabei an diesen Fragen:'''
| |
| <quiz display="simple">
| |
|
| |
|
| {'''Wie verändert sich die Streckenlänge <span style="text-decoration: overline;">ZB</span>?'''}
| |
| +Sie bleibt immer gleich.
| |
| -Sie ist variabel.
| |
|
| |
|
| {'''Wie verändert sich die Streckenlänge <span style="text-decoration: overline;">ZB'</span>?'''}
| |
| -Sie bleibt immer gleich.
| |
| +Sie ist variabel.
| |
|
| |
|
| {'''Wie verhält sich k?'''}
| | [[Bild:Porzelt_PanDiAuto.jpg|left|250px]] |
| -Es bleibt immer gleich.
| |
| +Es ist variabel.
| |
|
| |
|
| </quiz>
| | '''Panto und Dia machen eine Spritztour, um die zentrische Streckung im Alltag zu finden. Was die beiden entdeckt haben, siehst du auf der nächsten Seite.''' |
| |}
| |
| </div>
| |
| <br>
| |
| :Die Werte, die sich aus der Änderung von k ergeben, wurden in zwei Tabellen zusammengefasst.
| |
| :In der linken sind die Werte für k von 2 bis 0, in der rechten für k von -2 bis 0.
| |
| <br>
| |
| :'''Arbeitsauftrag:'''
| |
| :''1. Betrachte zunächst nur die linke Tabelle und stelle eine Vermutung auf, wie sich die Länge von <span style="text-decoration: overline;">ZB'</span> ändert im Vergleich zur Länge von <span style="text-decoration: overline;">ZB</span>?
| |
| :(Tipp: Betrachte auch den Wert von k!)
| |
| :''2. Vergleiche die Zeilen mit der selben Hintergrundfarbe! Was haben sie gemeinsam? Was sind die Unterschiede?''
| |
| {|
| |
| |
| |
| {| {{Prettytable}}
| |
| |- style="background-color:#8DB6CD"
| |
| ! k !! <span style="text-decoration: overline;">ZB</span> !! <span style="text-decoration: overline;">ZB'</span>
| |
| |- style="background-color:#CDB5CD"
| |
| ! 2 !! 4 !! 8
| |
| |- style="background-color:#CAFF70"
| |
| ! 1.5 !! 4 !! 6
| |
| |- style="background-color:#EEA2AD"
| |
| ! 1 !! 4 !! 4
| |
| |- style="background-color:#C6E2FF"
| |
| ! 0.5 !! 4 !! 2
| |
| |-
| |
| | 0 || 4 || 0
| |
| |}
| |
|
| |
|
| ||
| |
| {| {{Prettytable}}
| |
| |- style="background-color:#8DB6CD"
| |
| ! k !! <span style="text-decoration: overline;">ZB</span> !! <span style="text-decoration: overline;">ZB'</span>
| |
| |- style="background-color:#CDB5CD"
| |
| ! -2 !! 4 !! 8
| |
| |- style="background-color:#CAFF70"
| |
| ! -1.5 !! 4 !! 6
| |
| |- style="background-color:#EEA2AD"
| |
| ! -1 !! 4 !! 4
| |
| |- style="background-color:#C6E2FF"
| |
| ! -0.5 !! 4 !! 2
| |
| |-
| |
| | 0 || 4 || 0
| |
| |}
| |
| |}
| |
| <br>
| |
| :Hier kannst du deine Vermutung mit der von Dia vergleichen:
| |
| :{{Versteckt|
| |
| 1. <math>\overline{ZB'}</math> ist k-mal so lang wie <math>\overline{ZB}</math>.
| |
| 2. Die Längen der Strecken <math>\overline{ZB}</math> und <math>\overline{ZB'}</math> bleiben gleich, wenn sich das Vorzeichen von k ändert.}}
| |
| <br>
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| :'''Dia ist nach ihren Vermutungen total verwirrt. Sie versteht nicht warum der Wert von <span style="text-decoration: overline;">ZB'</span> gleich bleibt, wenn sich das Vorzeichen von k ändert.'''
| |
| :'''Vielleicht kannst du ihr helfen, indem du ihre Fragen beantwortest:'''
| |
| <br>
| |
| <quiz display="simple">
| |
|
| |
|
| {Kann eine Streckenlänge ein negatives Vorzeichen haben?} | | {{Fortsetzung|weiter=Exkurs: Weitere Beispiele einer zentrischen Streckung|weiterlink=/Weitere Beispiele}} |
| +nein
| |
| -ja
| |
|
| |
|
| {Wie kann man eine negative Zahl in eine positive Zahl umwandeln, sodass der Wert '''gleich''' bleibt,
| |
| sich jedoch aber eine positive Zahl '''nicht''' in eine negative Zahl umwandelt?}
| |
| -durch Quadrieren
| |
| +mit Hilfe von Betragsstrichen
| |
| -durch Multiplikation mit -1
| |
|
| |
|
| </quiz>
| |
| </div>
| |
| <br>
| |
| :Prima! Dank dir versteht jetzt Dia, wie die Werte für <span style="text-decoration: overline;">ZB'</span> entstehen.
| |
| :Mit deiner Hilfe und ihrer Vermutungen kann sie eine allgemeingültige Aussage machen.
| |
| :Teste durch Einsetzen der richtigen Wörter, ob auch du dahinter gekommen bist:
| |
| <div class="lueckentext-quiz">
| |
| Die Länge von '''<span style="text-decoration: overline;">ZB</span>''' ist '''|k|-mal''' so lang wie die Länge von '''<span style="text-decoration: overline;">ZB'</span>'''.
| |
| </div>
| |
|
| |
|
| <br>
| | [[Kategorie:Mathematik-digital]] |
| :Hier siehst du was das k bedeutet. Merke es dir, denn später wirst du darüber abgefragt!
| | [[Kategorie:Sekundarstufe 1]] |
| <div style="border: 2px solid #ffd700; background-color:#ffffff; padding:7px;">
| | [[Kategorie:Lernpfad]] |
| :'''k''' bezeichnet man als den '''Streckungsfaktor'''. Er gibt den Maßstab an, in dem das Bild vergrößert wurde.
| | [[Kategorie:Zentrische Streckung]] |
| </div>
| | [[Kategorie:Interaktive Übung]] |
| <br>
| | [[Kategorie:GeoGebra]] |
| | |
| ==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors==
| |
| :Wie du in der 2. Station schon herausgefunden hast ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.
| |
| :Geometrisch bedeutet dies für einen beliebigen Punkt P: <span style="text-decoration: overline;">ZP'</span> = |k| ∙ <span style="text-decoration: overline;">ZP</span>
| |
| :Daraus folgt: k=<math>{\overline{ZP'}\over\overline{ZP}}</math>
| |
| <br>
| |
| :Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden. <br>
| |
| :Setze dafür den richtigen Ausdruck in die passende Lücke:
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| {|
| |
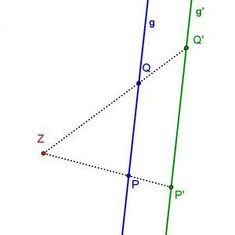
| |[[Bild:Porzelt_Streckenlänge.jpg]]||
| |
| <div class="lueckentext-quiz">
| |
| <span style="text-decoration: overline;">P'Q'</span> = |k| ∙ <span style="text-decoration: overline;">PQ</span> <br>
| |
| <math>\Leftrightarrow </math><span style="text-decoration: overline;">P'Q'</span> = '''|k|''' ∙ <span style="text-decoration: overline;">ZQ</span> - |k| ∙ '''<span style="text-decoration: overline;">ZP</span>'''<br>
| |
| <math>\Leftrightarrow </math><span style="text-decoration: overline;">P'Q'</span> = |k| ∙ ('''<span style="text-decoration: overline;">ZQ</span>''' - '''<span style="text-decoration: overline;">ZP</span>''')<br>
| |
| <math>\Leftrightarrow </math><span style="text-decoration: overline;">P'Q'</span> = |k| ∙ '''<span style="text-decoration: overline;">PQ</span>'''
| |
| </div>
| |
| |}
| |
| </div>
| |
| <br>
| |
| | |
| ==4. Station: Zusammenfassung==
| |
| :Hier siehst du alles, was du bisher herausgefunden hast zusammengefasst.
| |
| :Schreibe dir diese Zusammenfassung in dein Heft.
| |
| <div style="border: 2px solid #FF0000; background-color:#ffffff; padding:7px;">
| |
| '''Abbildungsvorschrift der zentrischen Streckung'''<br>
| |
| Wenn eine Vergrößerung von einem Zentrum ausgeht, dann spricht man von einer '''zentrischen Streckung'''. <br>
| |
| Sie wird festgelegt durch Angabe eines '''Streckungszentrums Z''' und eines '''Streckungsfaktors k'''. (Kurz: )<br>
| |
| Der '''Urpunkt P''', der '''Bildpunkt P'''' und das Streckungszentrum Z liegen auf einer Geraden. <br>
| |
| Es gilt: <span style="text-decoration: overline;">ZP'</span> = |k| ∙ <span style="text-decoration: overline;">ZP</span> <br>
| |
| Bei |k|>1 liegt eine Vergrößerung, bei 0<|k|<1 eine Verkleinerung vor. <br>
| |
| Wenn k=1 ist liegt die Identität vor, bei k= -1 eine Spiegelung. <br>
| |
| Für k>0 gilt: Urpunkt und Bildpunkt liegen auf der gleichen Seite von Z. <br>
| |
| Für k<0 gilt: Urpunkt und Bildpunkt liegen auf verschiedenen Seiten von Z. <br>
| |
| </div>
| |
| <br>
| |
| | |
| ==5. Station: Übungen==
| |
| ===1. Aufgabe===
| |
| <div class="schuettel-quiz">
| |
| :Das Bild zeigt eine '''zentrische''' '''Streckung'''.
| |
| </div>
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| {| <br>
| |
| |[[Bild:Porzelt_Taschenlampe_Quiz.jpg|center]]
| |
| |<div class="kreuzwort-quiz">
| |
| {|
| |
| |-
| |
| | Streckungsfaktor || Was kann man mit Hilfe des Schiebereglers (A) einstellen?
| |
| |-
| |
| | Streckungszentrum || Was stellt die Taschenlampe (B) dar?
| |
| |-
| |
| | Halbgerade || Was ist der Lichtstrahl (C)?
| |
| |-
| |
| | Urbild || Als was kann man den Strohhalm (D) noch bezeichnen?
| |
| |-
| |
| | Bild || Als was kann man den Schatten (E) noch bezeichnen?
| |
| |}
| |
| </div>
| |
| |}
| |
| </div>
| |
| <br>
| |
| | |
| ===2. Aufgabe===
| |
| :Berechne den Streckungsfaktor k in deinem Heft. Ordne danach die richtige Lösung zu:
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| {|
| |
| |[[Bild:Porzelt_Übungsaufgabe2.jpg]]||
| |
| <div class="lueckentext-quiz">
| |
| | |
| a) k= '''3''' <br>
| |
| b) k= '''-0,5'''<br>
| |
| c) k= '''0,4''' <br>
| |
| </div>
| |
| |}
| |
| </div>
| |
| <br>
| |
| | |
| ===3. Aufgabe===
| |
| :Trage für jede Teilaufgabe in einem Koordinatensystem die Ur- und Bildpunkte ein, verbinde sie wenn möglich
| |
| :und führe die zentrische Streckung mit gegebenem Zentrum und Streckungsfaktor durch.
| |
| <div style="border: 2px solid #00CD00; background-color:#ffffff; padding:7px;">
| |
| :a) Z(1|1), k= 2, P(2|1)
| |
| :b) Z(1|1), k= -2.5, P(3|1), Q(2|2)
| |
| :c) Z(1|1), k= 2.5, P(2|3), Q(4|1), R(4|3)
| |
| </div>
| |
| <br>
| |
| :Hier kannst du deine Lösung mit der von Dia vergleichen:
| |
| :{{Lösung versteckt|
| |
| '''a)'''[[Bild:Porzelt_Aufgabe3a.jpg]]
| |
| <br>
| |
| <br>
| |
| '''b)'''[[Bild:Porzelt_Aufgabe3b.jpg]]
| |
| <br>
| |
| <br>
| |
| '''c)'''[[Bild:Porzelt_Aufgabe3c.jpg]]
| |
| |}}
| |