Benutzer:Cloehner/Dreiecke und Winkel/Winkel an Geradenkreuzungen: Unterschied zwischen den Versionen
Benutzer:Cloehner/Dreiecke und Winkel/Winkel an Geradenkreuzungen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung |
||
| (20 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
<ggb_applet id="typj8ed7" width="426" height="506" border="888888" /> | <ggb_applet id="typj8ed7" width="426" height="506" border="888888" /> | ||
Darstellungsprobleme? Öffne [https://ggbm.at/DUNktpEg diesen Link] in einem neuen Tab. | |||
{{Aufgaben|1=1|2=<math>\alpha</math> und <math>\beta</math> sind Nebenwinkel. Gib die fehlende Winkelgröße an! | {{Aufgaben|1=1|2=<math>\alpha</math> und <math>\beta</math> sind Nebenwinkel. Gib die fehlende Winkelgröße an! | ||
| Zeile 14: | Zeile 16: | ||
<math>\alpha</math> = 113°, <math>\beta</math> = '''67()'''° | <math>\alpha</math> = 113°, <math>\beta</math> = '''67()'''° | ||
<math>\alpha</math> = '''89()'''° <math>\beta</math> = 91° | <math>\alpha</math> = '''89()'''°, <math>\beta</math> = 91° | ||
<math>\alpha</math> = '''26()'''°, <math>\beta</math> = 154° | |||
</div>}} | |||
{{Aufgaben|2|Formuliere den Zusammenhang, den du zum Berechnen der Winkelgröße verwendet hast, auf dem Arbeitsblatt und fertige dort eine Skizze an, in der zwei Nebenwinkel erkennbar sind.}} | |||
==Scheitelwinkel== | |||
Im Applet wurden zwei '''Scheitelwinkel''' markiert. Verändere die Größe der Winkel, indem du die markierten Punkte verschiebst, bis du sicher bist, dass du den Zusammenhang erkannt hast. | |||
<ggb_applet id="VzsHg2zT" width="800" height="503" border="888888" /> | |||
Darstellungsprobleme? Öffne [https://ggbm.at/VzsHg2zT diesen Link] in einem neuen Tab. | |||
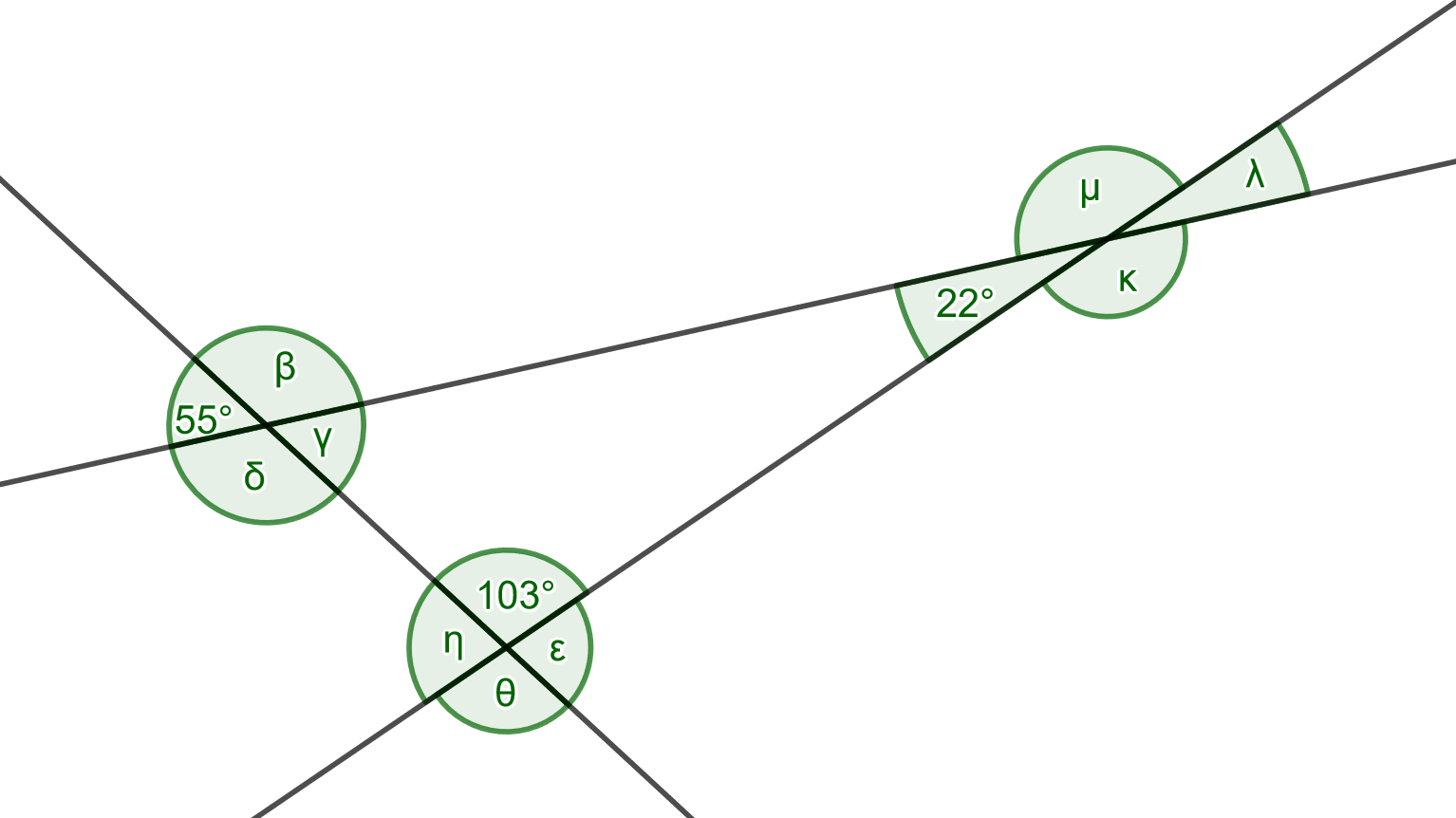
{{Aufgaben|1=3|2=Gib die Größen der fehlenden Winkel an. | |||
[[Datei:NSW.png|Neben- und Scheitelwinkel]] | |||
<div class="lueckentext-quiz"> | |||
<math>\beta</math> = '''125()'''° | |||
<math>\gamma</math> = '''55()'''° | |||
<math>\ | <math>\delta</math> = '''125()'''° | ||
<math>\varepsilon</math> = '''77()'''° | |||
<math>\eta</math> = '''77()'''° | |||
<math>\theta</math> = '''103()'''° | |||
<math>\lambda</math> = '''22()'''° | |||
<math>\mu</math> = '''158()'''° | |||
<math>\kappa</math> = '''158()'''° | |||
</div>}} | </div>}} | ||
{{Aufgaben|4|Formuliere den Zusammenhang bei Scheitelwinkeln auf deinem Arbeitsblatt und fertige dort eine Skizze an.}} | |||
==Wechselwinkel== | |||
In der Abbildung siehst du zwei verschiedene Varianten von Wechselwinkeln. Verändere die Größen der Winkel, indem du die markierten Punkte verschiebst, bis du den Zusammenhang erkannt hast. Wo liegen Gemeinsakeiten und Unterschiede der beiden verschiedenen Varianten von Wechselwinkeln? | |||
<ggb_applet id="s7apphv5" width="700" height="350" border="888888" /> | |||
Darstellungsprobleme? Öffne [https://ggbm.at/a7upfsjz diesen Link] in einem neuen Tab. | |||
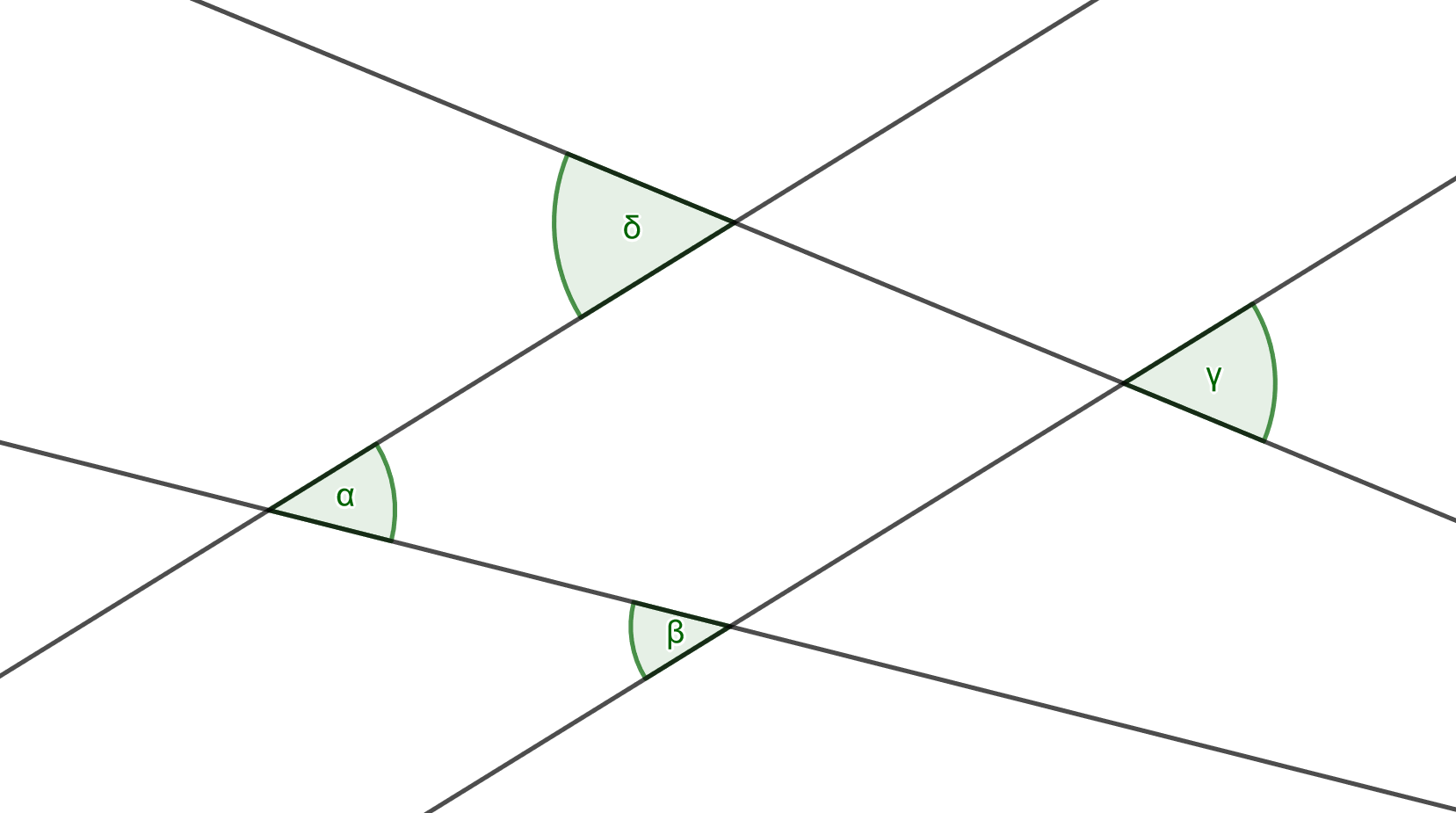
{{Aufgaben|1=5|2=Wähle die richtigen Antworten aus! | |||
[[Datei:WW.png|Wechselwinkel]] | |||
<div class="multiplechoice-quiz"> | |||
Welche Winkel sind so groß wie <math>\beta</math>? (<math>\alpha</math>) (!<math>\gamma</math>) (!<math>\delta</math>) | |||
Welche Winkel sind wo groß wie <math>\gamma</math>? (!<math>\alpha</math>) (!<math>\beta</math>) (<math>\delta</math>) | |||
</div>}} | |||
{{Aufgaben|6|Formuliere den Zusammenhang bei Wechselwinkeln auf deinem Arbeitsblatt und fertige dort eine Skizze an. Welche Bedingung müssen die Geraden erfüllen, damit Wechselwinkel gleich groß sind?}} | |||
==Stufenwinkel== | |||
In der Abbildung kannst du verschiedene Stufenwinkel anzeigen lassen. Verändere die Größen der Winkel, indem du die markierten Punkte verschiebst, bis du den Zusammenhang erkannt hast. | |||
<ggb_applet id="N3an3wcs" width="680" height="680" border="888888" /> | |||
Darstellungsprobleme? Öffne [https://ggbm.at/N3an3wcs diesen Link] in einem neuen Tab. | |||
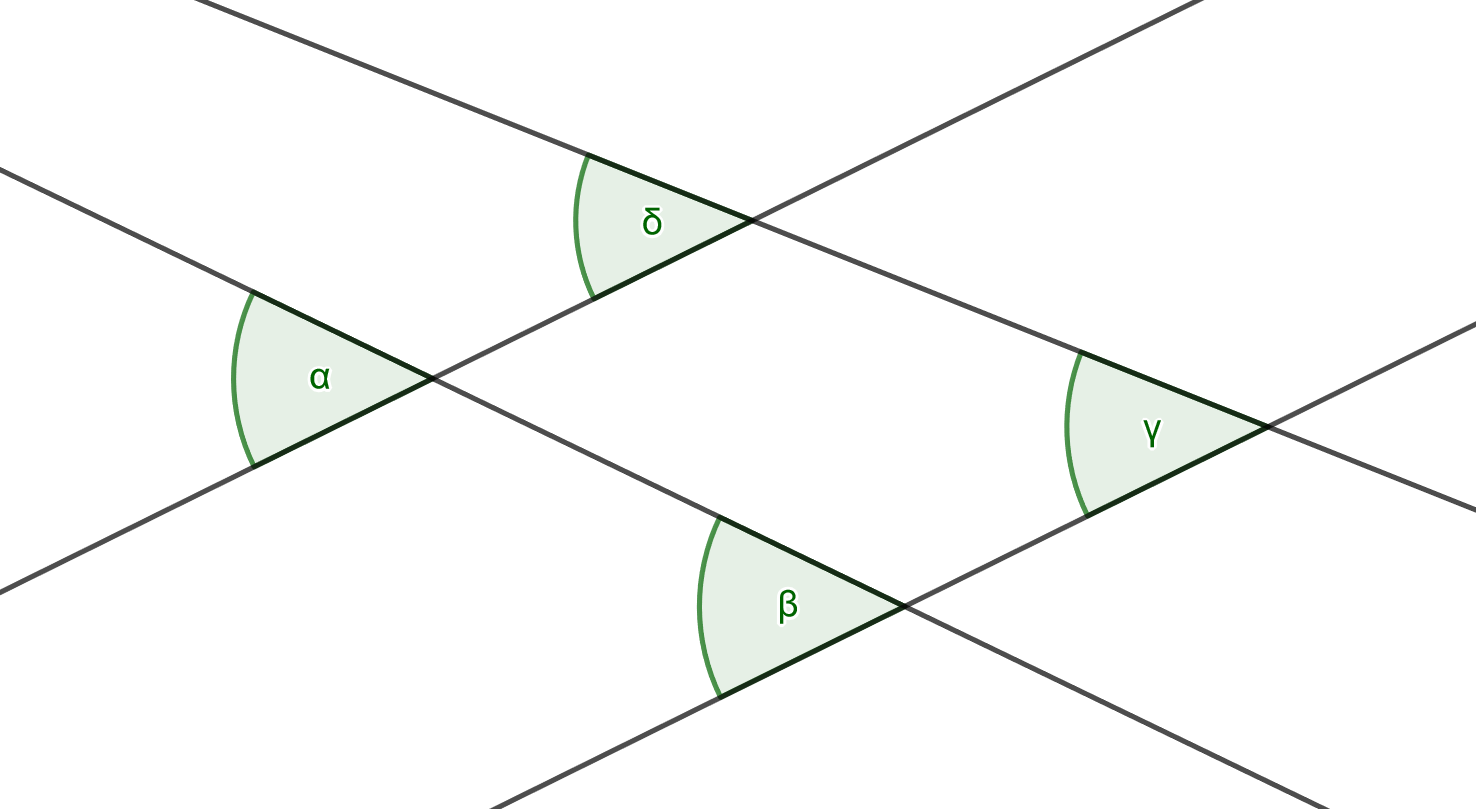
{{Aufgaben|1=7|2=Wähle die richtigen Antworten aus! | |||
[[Datei:F-Winkel.png|Stufenwinkel]] | |||
<div class="multiplechoice-quiz"> | |||
Welche Winkel sind so groß wie <math>\alpha</math>? (<math>\beta</math>) (!<math>\gamma</math>) (!<math>\delta</math>) | |||
Welche Winkel sind wo groß wie <math>\delta</math>? (!<math>\alpha</math>) (!<math>\beta</math>) (<math>\gamma</math>) | |||
</div>}} | |||
{{Aufgaben|8|Formuliere den Zusammenhang bei Stufenwinkeln auf deinem Arbeitsblatt und fertige dort eine Skizze an. Welche Bedingung müssen die Geraden erfüllen, damit Stufenwinkel gleich groß sind?}} | |||
==Überprüfe dein Wissen== | |||
{{Aufgaben|9|Bearbeite die Aufgabe. Überlege dir die Größen der markierten Winkel zunächst selbst und ''notiere sie auf einem Schmierzettel''. Nutze die Schaltflächen links nur zur Kontrolle oder wenn du wirklich nicht mehr weiter weißt! | |||
<ggb_applet id="hYtzhFqX" width="900" height="500" border="888888" />}} | |||
Darstellungsprobleme? Öffne [https://ggbm.at/hYtzhFqX diesen Link] in einem neuen Tab. | |||
{{Fortsetzung|weiter=Nächster Abschnitt: Die Winkelsumme im Dreieck|weiterlink=Benutzer:Cloehner/Dreiecke und Winkel/Die Winkelsumme im Dreieck}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:Winkel]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 24. April 2022, 10:44 Uhr
In diesem Kapitel wirst du dich mit verschiedenen Zusammenhängen zwischen den Größen von Winkeln an Geradenkreuzungen auseinandersetzen. Manche Winkelbeziehungen waren dir vielleicht schon bekannt, einige werden für dich neu sein. Protokolliere alle Zusammenhänge, die du auf dieser Seite entdeckt hast, auf dem Arbeitsblatt 
Winkel an Geradenkreuzungen.
Nebenwinkel
Im Applet wurden zwei Nebenwinkel markiert. Ändere die Größen der Winkel, indem du die eingezeichneten Punkte verschiebst, bis du einen Zusammenhang erkannt hast.
Darstellungsprobleme? Öffne diesen Link in einem neuen Tab.
und sind Nebenwinkel. Gib die fehlende Winkelgröße an!
= 60°, = 120()°
= 113°, = 67()°
= 89()°, = 91°
= 26()°, = 154°
Scheitelwinkel
Im Applet wurden zwei Scheitelwinkel markiert. Verändere die Größe der Winkel, indem du die markierten Punkte verschiebst, bis du sicher bist, dass du den Zusammenhang erkannt hast.
Darstellungsprobleme? Öffne diesen Link in einem neuen Tab.
Gib die Größen der fehlenden Winkel an.
= 125()°
= 55()°
= 125()°
= 77()°
= 77()°
= 103()°
= 22()°
= 158()°
= 158()°
Wechselwinkel
In der Abbildung siehst du zwei verschiedene Varianten von Wechselwinkeln. Verändere die Größen der Winkel, indem du die markierten Punkte verschiebst, bis du den Zusammenhang erkannt hast. Wo liegen Gemeinsakeiten und Unterschiede der beiden verschiedenen Varianten von Wechselwinkeln?
Darstellungsprobleme? Öffne diesen Link in einem neuen Tab.
Wähle die richtigen Antworten aus!
Welche Winkel sind so groß wie ? () (!) (!)
Welche Winkel sind wo groß wie ? (!) (!) ()
Stufenwinkel
In der Abbildung kannst du verschiedene Stufenwinkel anzeigen lassen. Verändere die Größen der Winkel, indem du die markierten Punkte verschiebst, bis du den Zusammenhang erkannt hast.
Darstellungsprobleme? Öffne diesen Link in einem neuen Tab.
Wähle die richtigen Antworten aus!
Welche Winkel sind so groß wie ? () (!) (!)
Welche Winkel sind wo groß wie ? (!) (!) ()
Überprüfe dein Wissen
Bearbeite die Aufgabe. Überlege dir die Größen der markierten Winkel zunächst selbst und notiere sie auf einem Schmierzettel. Nutze die Schaltflächen links nur zur Kontrolle oder wenn du wirklich nicht mehr weiter weißt!
Darstellungsprobleme? Öffne diesen Link in einem neuen Tab.
