Quadratische Funktionen erkunden/Von der Scheitelpunkt- zur Normalform: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
{{Navigation verstecken|{{Quadratische Funktionen erkunden}}|Lernschritte einblenden|Lernschritte ausblenden}}
{{Navigation verstecken|{{Quadratische Funktionen erkunden}}|Lernschritte einblenden|Lernschritte ausblenden}}
__NOTOC__
__NOTOC__
{{Box| |In diesem Kapitel kannst du herausfinden, wie du quadratischen Funktionen in '''Scheitelpunktform''' in quadratische Funktionen in '''Normalform''' umwandeln kannst. |Kurzinfo}}
{{Box| |In diesem Kapitel kannst du herausfinden, wie du quadratische Funktionen in '''Scheitelpunktform''' in quadratische Funktionen in '''Normalform''' umwandeln kannst. |Kurzinfo}}




Zeile 47: Zeile 47:
|}
|}


<div class="box arbeitsmethode">
=== Aufgabe 1 ===


'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 15)''' [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].
{{Box|Aufgabe 1|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 15)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].


'''a)''' Lies dir das Beispiel oben durch und versuche es nachzuvollziehen.  
'''a)''' Lies dir das Beispiel oben durch und versuche es nachzuvollziehen.  


'''b)''' Nimm deine Lösung zu der [[Mathematik-digital/Quadratische Funktionen erkunden/Die Scheitelpunktform|1. Aufgabe bei der Scheitelpunktform]] in deinen Hefter (S. 9) und wähle zwei deiner Terme aus. Multipliziere diese Funktionsterme wie im Beispiel aus und notiere deine Rechnung.
'''b)''' Nimm deine Lösung zu der [[Mathematik-digital/Quadratische Funktionen erkunden/Die Scheitelpunktform|1. Aufgabe bei der Scheitelpunktform]] in deinem Hefter (S. 9) und wähle zwei deiner Terme aus. Multipliziere diese Funktionsterme wie im Beispiel aus und notiere deine Rechnung.


'''c)''' Vergleiche die Ergebnisse deiner Ausmultiplikation mit deinen Termen für die [[Mathematik-digital/Quadratische Funktionen erkunden/Die Normalform|4. Aufgabe bei der Normalform]] (S.14).
'''c)''' Vergleiche die Ergebnisse deiner Ausmultiplikation mit deinen Termen für die [[Mathematik-digital/Quadratische Funktionen erkunden/Die Normalform|4. Aufgabe bei der Normalform]] (S.14).
<div class="mw-collapsible mw-collapsed" data-expandtext="Hinweis" data-collapsetext="Hinweis verbergen">
{{Lösung versteckt|Es kann sein, dass dein Ergebnis etwas von deinem eigenem Normalformterm abweicht. Das liegt dann daran, dass du die Parabel bei der Aufgabe auf der Normalformseite nicht genau gleich in das Bild gelegt hast wie auf der Scheitelpunktseite. Du solltest dich jedoch in dem angegebenen Spielraumbereich der Lösungsvorschläge befinden.|Hinwes anzeigen|Hinweis verbergen}}
Es kann sein, dass dein Ergebnis etwas von deinem eigenem Normalformterm abweicht. Das liegt dann daran, dass du die Parabel bei der Aufgabe auf der Normalformseite nicht genau gleich in das Bild gelegt hast wie auf der Scheitelpunktseite. Du solltest dich jedoch in dem angegebenen Spielraumbereich der Lösungsvorschläge befinden.
{{Lösung versteckt|1=
</div>
{{{!}} class="wikitable"
{{!}}-
!'''Funktionsterm Angry Birds'''!!'''Schritt-für-Schritt-Anleitung'''!!'''Funktionsterm Golden Gate Bridge'''!!'''Schritt-für-Schritt-Anleitung'''
{{!}}-
{{!}}<math>f(x)=-0,13(x-7)^2+4,85</math>{{!}}{{!}}Klammer auflösen{{!}}{{!}}<math>f(x)=0,04(x-5,7)^2+1</math>{{!}}{{!}}Klammer auflösen
{{!}}-
{{!}}<math>=-0,13((x-7)\cdot(x-7))+4,85</math>{{!}}{{!}}innere Klammer ausmultiplizieren{{!}}{{!}}<math>=0,04((x-5,7)\cdot(x-5,7))+1</math>{{!}}{{!}}innere Klammer ausmultiplizieren
{{!}}-
{{!}}<math>=-0,13(x^2-14x+49)+4,85</math>{{!}}{{!}}Klammer ausmultiplizieren{{!}}{{!}}<math>=0,04(x^2-11,4x+32,49)+1</math>{{!}}{{!}}Klammer ausmultiplizieren
{{!}}-
{{!}}<math>=-0,13x^2+1,82x-6,37+4,85</math>{{!}}{{!}}Zusammenfassen{{!}}{{!}}<math>=0,04x^2-0,456x+1,3+1</math>{{!}}{{!}}Zusammenfassen
{{!}}-
{{!}}<math>=-0,13x^2+1,82x-1,52</math>{{!}}{{!}}&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;{{!}}{{!}}<math>=0,04x^2-0,456x+2,3</math>
{{!}}}


<div class="mw-collapsible mw-collapsed" data-expandtext="Lösungsvorschläge anzeigen" data-collapsetext="Lösungsvorschläge verbergen">
{{{!}} class="wikitable"
{|
{{!}}-
|-
!'''Funktionsterm Springbrunnen'''!!'''Schritt-für-Schritt-Anleitung'''!!'''Funktionsterm Elbphilharmonie (links)'''!!'''Schritt-für-Schritt-Anleitung'''
|'''Funktionsterm Angry Birds'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''&nbsp;&nbsp;||'''Funktionsterm Golden Gate Bridge'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''
{{!}}-
|-
{{!}}<math>f(x)=-0,33(x-4,85)^2+5,3</math>{{!}}{{!}}Klammer auflösen{{!}}{{!}}<math>f(x)=0,4(x-2,5)^2+4,35</math>{{!}}{{!}}Klammer auflösen
|
{{!}}-
|-
{{!}}<math>=-0,33((x-4,85)\cdot(x-4,85))+5,3</math>{{!}}{{!}}innere Klammer ausmultiplizieren{{!}}{{!}}<math>=0,4((x-2,5)\cdot(x-2,5))+4,35</math>{{!}}{{!}}innere Klammer ausmultiplizieren
|
{{!}}-
|-
{{!}}<math>=-0,33(x^2-9,7x+23,52)+5,3</math>{{!}}{{!}}Klammer ausmultiplizieren{{!}}{{!}}<math>=0,4(x^2-5x+6,25)+4,35</math>{{!}}{{!}}Klammer ausmultiplizieren
|<math>f(x)=-0,13(x-7)^2+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen&nbsp;&nbsp;||<math>f(x)=0,04(x-5,7)^2+1</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
{{!}}-
|-
{{!}}<math>=-0,33x^2+3,2x-6,37-7,76</math>{{!}}{{!}}Zusammenfassen{{!}}{{!}}<math>=0,4x^2-2x+2,5+4,35</math>{{!}}{{!}}Zusammenfassen
|
{{!}}-
|-
{{!}}<math>=-0,33x^2+3,2x-2,46</math>{{!}}{{!}}&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;{{!}}{{!}}<math>=0,4x^2-2x+6,85</math>
|
{{!}}}
|-
|<math>=-0,13((x-7)\cdot(x-7))+4,85</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=0,04((x-5,7)\cdot(x-5,7))+1</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=-0,13(x^2-14x+49)+4,85</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=0,04(x^2-11,4x+32,49)+1</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=-0,13x^2+1,82x-6,37+4,85</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen&nbsp;&nbsp;||<math>=0,04x^2-0,456x+1,3+1</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen
|-
|
|-
|
|-
|<math>=-0,13x^2+1,82x-1,52</math>||&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;||<math>=0,04x^2-0,456x+2,3</math>
|}


{{{!}} class="wikitable"
{{!}}-
!'''Funktionsterm Elbphilharmonie (mitte)'''!!'''Schritt-für-Schritt-Anleitung'''!!'''Funktionsterm Elbphilharmonie (rechts)'''!!'''Schritt-für-Schritt-Anleitung'''
{{!}}-
{{!}}<math>f(x)=0,33(x-5,85)^2+3,4</math>{{!}}{{!}}Klammer auflösen{{!}}{{!}}<math>f(x)=0,22(x-9,4)^2+3,6</math>{{!}}{{!}}Klammer auflösen
{{!}}-
{{!}}<math>=0,33((x-5,85)\cdot(x-5,85))+3,4</math>{{!}}{{!}}innere Klammer ausmultiplizieren{{!}}{{!}}<math>=0,22((x-9,4)\cdot(x-9,4))+3,6</math>{{!}}{{!}}innere Klammer ausmultiplizieren
{{!}}-
{{!}}<math>=0,33(x^2-11,7x+34,22)+3,4</math>{{!}}{{!}}Klammer ausmultiplizieren{{!}}{{!}}<math>=0,22(x^2-18,8x+88,36)+3,6</math>{{!}}{{!}}Klammer ausmultiplizieren
{{!}}-
{{!}}<math>=0,33x^2-3,86x+11,29+3,4</math>{{!}}{{!}}Zusammenfassen{{!}}{{!}}<math>=0,22x^2-4,14x+19,44+3,6</math>{{!}}{{!}}Zusammenfassen
{{!}}-
{{!}}<math>=0,33x^2+3,86x+14,69</math>{{!}}{{!}}&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;{{!}}{{!}}<math>=0,22x^2-4,14x+23,04</math>
{{!}}}


{|
{{{!}} class="wikitable"
|-
{{!}}-
|'''Funktionsterm Springbrunnen'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''&nbsp;&nbsp;||'''Funktionsterm Elbphilharmonie (links)'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''
!'''Funktionsterm Gebirge'''!!'''Schritt-für-Schritt-Anleitung'''!!'''Funktionsterm Motorrad'''!!'''Schritt-für-Schritt-Anleitung'''
|-
{{!}}-
|
{{!}}<math>f(x)=-0,2(x-5,4)^2+2,3</math>{{!}}{{!}}Klammer auflösen{{!}}{{!}}<math>f(x)=-0,07(x-7,7)^2+5,95</math>{{!}}{{!}}Klammer auflösen
|-
{{!}}-
|
{{!}}<math>=-0,2((x-5,4)\cdot(x-5,4))+2,3</math>{{!}}{{!}}innere Klammer ausmultiplizieren{{!}}{{!}}<math>=-0,07((x-7,7)\cdot(x-7,7))+5,95</math>{{!}}{{!}}innere Klammer ausmultiplizieren
|-
{{!}}-
|<math>f(x)=-0,33(x-4,85)^2+5,3</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen&nbsp;&nbsp;||<math>f(x)=0,4(x-2,5)^2+4,35</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
{{!}}<math>=-0,2(x^2-10,8x+29,16)+2,3</math>{{!}}{{!}}Klammer ausmultiplizieren{{!}}{{!}}<math>=-0,07(x^2-15,4x+59,29)+5,95</math>{{!}}{{!}}Klammer ausmultiplizieren
|-
{{!}}-
|
{{!}}<math>=-0,2x^2+2,16x-5,83+2,3</math>{{!}}{{!}}Zusammenfassen{{!}}{{!}}<math>=-0,07x^2+1,08x-4,15+5,95</math>{{!}}{{!}}Zusammenfassen
|-
{{!}}-
|
{{!}}<math>=-0,2x^2+2,16x-3,53</math>{{!}}{{!}}&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;{{!}}{{!}}<math>=-0,07x^2+1,08x+1,79</math>
|-
{{!}}}|2=Lösungsvorschlag anzeigen|3=Lösungsvorschlag verbergen}}
|<math>=-0,33((x-4,85)\cdot(x-4,85))+5,3</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=0,4((x-2,5)\cdot(x-2,5))+4,35</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|Arbeitsmethode
|-
}}
|
|-
|
|-
|<math>=-0,33(x^2-9,7x+23,52)+5,3</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=0,4(x^2-5x+6,25)+4,35</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=-0,33x^2+3,2x-6,37-7,76</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen&nbsp;&nbsp;||<math>=0,4x^2-2x+2,5+4,35</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen
|-
|
|-
|
|-
|<math>=-0,33x^2+3,2x-2,46</math>||&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;||<math>=0,4x^2-2x+6,85</math>
|}
 
 
{|
|-
|'''Funktionsterm Elbphilharmonie (mitte)'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''&nbsp;&nbsp;||'''Funktionsterm Elbphilharmonie (rechts)'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''
|-
|
|-
|
|-
|<math>f(x)=0,33(x-5,85)^2+3,4</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen&nbsp;&nbsp;||<math>f(x)=0,22(x-9,4)^2+3,6</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
|-
|
|-
|
|-
|<math>=0,33((x-5,85)\cdot(x-5,85))+3,4</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=0,22((x-9,4)\cdot(x-9,4))+3,6</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=0,33(x^2-11,7x+34,22)+3,4</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=0,22(x^2-18,8x+88,36)+3,6</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=0,33x^2-3,86x+11,29+3,4</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen&nbsp;&nbsp;||<math>=0,22x^2-4,14x+19,44+3,6</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen
|-
|
|-
|
|-
|<math>=0,33x^2+3,86x+14,69</math>||&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;||<math>=0,22x^2-4,14x+23,04</math>
|}
 
 
{|
|-
|'''Funktionsterm Gebirge'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''&nbsp;&nbsp;||'''Funktionsterm Motorrad'''||&nbsp;&nbsp;&nbsp;'''Schritt-für-Schritt-Anleitung'''
|-
|
|-
|
|-
|<math>f(x)=-0,2(x-5,4)^2+2,3</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen&nbsp;&nbsp;||<math>f(x)=-0,07(x-7,7)^2+5,95</math>||&nbsp;&nbsp;&nbsp;Klammer auflösen
|-
|
|-
|
|-
|<math>=-0,2((x-5,4)\cdot(x-5,4))+2,3</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=-0,07((x-7,7)\cdot(x-7,7))+5,95</math>||&nbsp;&nbsp;&nbsp;innere Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=-0,2(x^2-10,8x+29,16)+2,3</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren&nbsp;&nbsp;||<math>=-0,07(x^2-15,4x+59,29)+5,95</math>||&nbsp;&nbsp;&nbsp;Klammer ausmultiplizieren
|-
|
|-
|
|-
|<math>=-0,2x^2+2,16x-5,83+2,3</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen&nbsp;&nbsp;||<math>=-0,07x^2+1,08x-4,15+5,95</math>||&nbsp;&nbsp;&nbsp;Zusammenfassen
|-
|
|-
|
|-
|<math>=-0,2x^2+2,16x-3,53</math>||&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;||<math>=-0,07x^2+1,08x+1,79</math>
|}
</div></div>


Das folgende Applet kannst du nutzen, um deine Ergebnisse aus Aufgabe 1 zu kontrollieren. Außerdem kannst du mit den Parametern beider Darstellungsformen experimentieren und zum Beispiel untersuchen, wie du die Parameterwerte verändern musst, um beide Graphen an einer beliebigen Stelle im Koordinatensystem übereinander zu legen.
Das folgende Applet kannst du nutzen, um deine Ergebnisse aus Aufgabe 1 zu kontrollieren. Außerdem kannst du mit den Parametern beider Darstellungsformen experimentieren und zum Beispiel untersuchen, wie du die Parameterwerte verändern musst, um beide Graphen an einer beliebigen Stelle im Koordinatensystem übereinander zu legen.


<ggb_applet id="R9CvVq59" width="800" height="570" border="888888" />
<ggb_applet id="R9CvVq59" width="800" height="570" border="888888" />


==Erklärvideo==
==Erklärvideo==
Zeile 220: Zeile 134:




==Achtung: Parameter c <math>\neq</math> Parameter e==
==Achtung: Parameter <math>c</math> und Parameter <math>e</math> im Vergleich==
<div class="box arbeitsmethode">
{{Box|Aufgabe 2|
=== Aufgabe 2 ===
'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 15-16)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].
'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 15)''' [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].


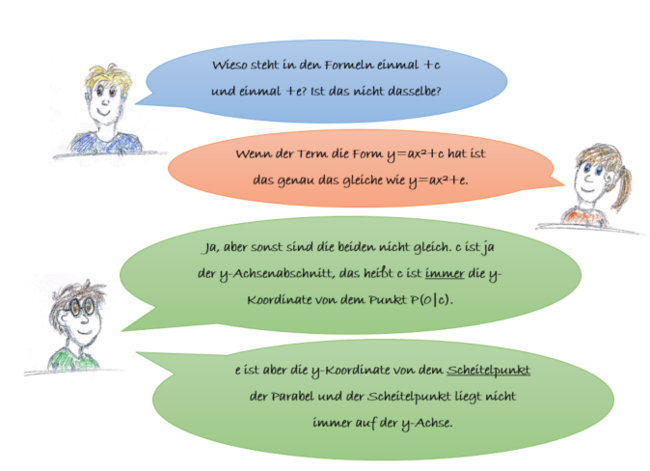
[[Datei:Unterhaltung c ungleich e.PNG|rahmenlos|650px|Parameter QF]]
[[Datei:Unterhaltung c ungleich e.PNG|rahmenlos|650px|Parameter QF]]


'''a)''' Lies dir die Unterhaltung von Fabian, Merle und Lucio durch. Zeichne zwei Parabeln in deinen Hefter bei denen (1) die Parameter <math>c</math> und <math>e</math> gleich sind bzw. (2) die Parameter  <math>c</math> und <math>e</math> nicht gleich sind.
'''a)''' Lies dir die Unterhaltung von Fabian, Merle und Lucio durch.  


'''b)''' Gib jeweils die Werte für <math>c</math> und <math>e</math> an.
'''b)''' Denke dir zwei Funktionsterme quadratischer Funktionen aus für die gilt: (1) <math>c=e</math> bzw. (2) <math>c \neq e</math>. Gib jeweils die Werte für <math>c</math> und <math>e</math> an.


 
'''c)''' Zeichne die Parabeln zu deinen Funktionstermen aus b) in ein Koordinatensystem.
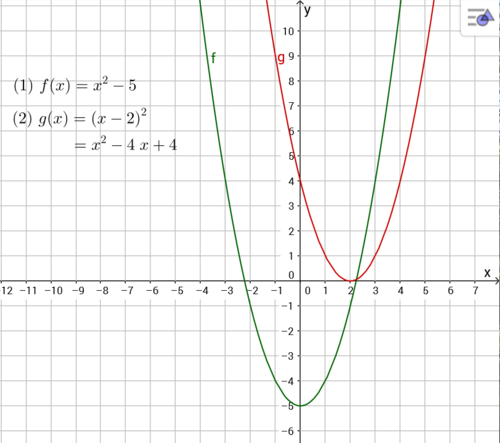
<div class="mw-collapsible mw-collapsed" data-expandtext="Beispiellösung" data-collapsetext="verbergen">
{{Lösung versteckt|Dein Ergebnis kann zum Beispiel so aussehen:
Dein Ergebnis kann zum Beispiel so aussehen:


[[Datei:Beispiellösung Parameter c und e.PNG|rahmenlos|500px|Beispiel]]
[[Datei:Beispiellösung Parameter c und e.PNG|rahmenlos|500px|Beispiel]]
Zeile 241: Zeile 153:
Bei <math>g(x)=(x-2)^2=x^2-4x+4</math> ist <math>c=4</math> und <math>e=0</math>.
Bei <math>g(x)=(x-2)^2=x^2-4x+4</math> ist <math>c=4</math> und <math>e=0</math>.


</div></div>


Nutze das GeoGebra-Applet um deine eigene Lösung zu kontrollieren:
Nutze das GeoGebra-Applet um deine eigene Lösung zu kontrollieren:


<ggb_applet id="DRDCQZvn" width="700" height="500" border="888888" />
<ggb_applet id="DRDCQZvn" width="700" height="500" border="888888" />|Lösung anzeigen|Lösung verbergen}}
|Arbeitsmethode
}}
 


==Merksätze==
==Merksätze==
{{Box|Aufgabe3|
{{Box|Aufgabe 3|Lies dir die folgenden Merksätze aufmerksam durch.
'''Für diese Aufgabe benötigst du deinen Hefter (Merkliste, S. 5-6)''' [[Datei:Notepad-117597.svg|40px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]].
 
Ergänze die Merksätze jeweils durch ein Beispiel.
|Arbeitsmethode}}
|Arbeitsmethode}}


Zeile 274: Zeile 185:


Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]])
Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]])
[[Kategorie:Mathematik]]
 
[[Kategorie:ZUM2Edutags]]
[[Kategorie:Quadratische Funktion]]
[[Kategorie:Quadratische Funktion]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:Interaktive Übung]]
[[Kategorie:GeoGebra]]
[[Kategorie:GeoGebra]]

Aktuelle Version vom 30. März 2022, 21:39 Uhr

gRIFIKBERSCHREIBUNG)

Quadratische Funktionen erkunden

< Mathematik-digital

In diesem Kapitel kannst du herausfinden, wie du quadratische Funktionen in Scheitelpunktform in quadratische Funktionen in Normalform umwandeln kannst.


Beispiel

Für den Basketballwurf konnten näherungsweise diese beiden Funktionsterme gefunden werden:

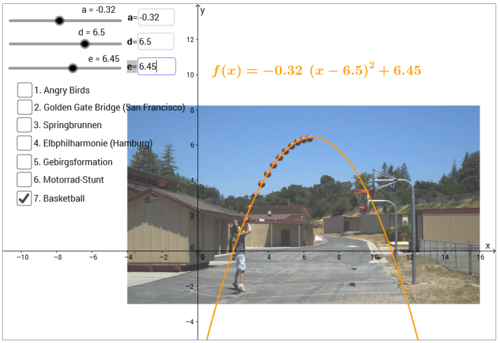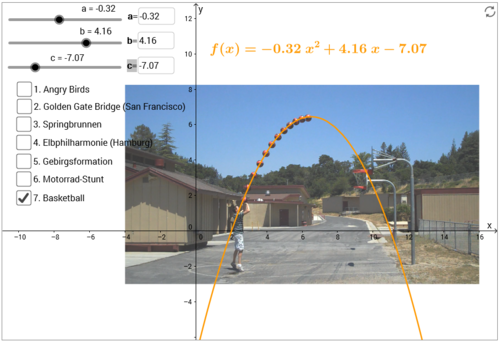
Basketballwurf Parabel Basketballwurf Parabel

Die Funktionsterme müssen irgendwie ineinander überführbar sein, da sie die gleiche Parabel beschreiben.

Durch Ausmultiplikation der Scheitelpunktform erhalten wir:


Funktionsterm    Schritt-für-Schritt-Anleitung
   Klammer auflösen
   innere Klammer ausmultiplizieren
   Klammer ausmultiplizieren
   Zusammenfassen


Ein Blick auf das zweite Bild oben zeigt, dass das Ergebnis der Ausmultiplikation genau der Term in Normalform ist. |}


Aufgabe 1

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 15) Notizblock mit Bleistift.

a) Lies dir das Beispiel oben durch und versuche es nachzuvollziehen.

b) Nimm deine Lösung zu der 1. Aufgabe bei der Scheitelpunktform in deinem Hefter (S. 9) und wähle zwei deiner Terme aus. Multipliziere diese Funktionsterme wie im Beispiel aus und notiere deine Rechnung.

c) Vergleiche die Ergebnisse deiner Ausmultiplikation mit deinen Termen für die 4. Aufgabe bei der Normalform (S.14).

Es kann sein, dass dein Ergebnis etwas von deinem eigenem Normalformterm abweicht. Das liegt dann daran, dass du die Parabel bei der Aufgabe auf der Normalformseite nicht genau gleich in das Bild gelegt hast wie auf der Scheitelpunktseite. Du solltest dich jedoch in dem angegebenen Spielraumbereich der Lösungsvorschläge befinden.
Funktionsterm Angry Birds Schritt-für-Schritt-Anleitung Funktionsterm Golden Gate Bridge Schritt-für-Schritt-Anleitung
Klammer auflösen Klammer auflösen
innere Klammer ausmultiplizieren innere Klammer ausmultiplizieren
Klammer ausmultiplizieren Klammer ausmultiplizieren
Zusammenfassen Zusammenfassen
     
Funktionsterm Springbrunnen Schritt-für-Schritt-Anleitung Funktionsterm Elbphilharmonie (links) Schritt-für-Schritt-Anleitung
Klammer auflösen Klammer auflösen
innere Klammer ausmultiplizieren innere Klammer ausmultiplizieren
Klammer ausmultiplizieren Klammer ausmultiplizieren
Zusammenfassen Zusammenfassen
     
Funktionsterm Elbphilharmonie (mitte) Schritt-für-Schritt-Anleitung Funktionsterm Elbphilharmonie (rechts) Schritt-für-Schritt-Anleitung
Klammer auflösen Klammer auflösen
innere Klammer ausmultiplizieren innere Klammer ausmultiplizieren
Klammer ausmultiplizieren Klammer ausmultiplizieren
Zusammenfassen Zusammenfassen
     
Funktionsterm Gebirge Schritt-für-Schritt-Anleitung Funktionsterm Motorrad Schritt-für-Schritt-Anleitung
Klammer auflösen Klammer auflösen
innere Klammer ausmultiplizieren innere Klammer ausmultiplizieren
Klammer ausmultiplizieren Klammer ausmultiplizieren
Zusammenfassen Zusammenfassen
     

Das folgende Applet kannst du nutzen, um deine Ergebnisse aus Aufgabe 1 zu kontrollieren. Außerdem kannst du mit den Parametern beider Darstellungsformen experimentieren und zum Beispiel untersuchen, wie du die Parameterwerte verändern musst, um beide Graphen an einer beliebigen Stelle im Koordinatensystem übereinander zu legen.

GeoGebra


Erklärvideo

Daniel Jung hat auf Youtube in seinem Channel Mathe by Daniel Jung zu den verschiedensten Themen Erklärvideos erstellt.

Falls dir die Umformung von der Scheitelpunkt- auf die Normalform schwer fiel, kannst du dir hier ein Video dazu anschauen und es dann noch einmal probieren. Denke daran dir Kopfhörer anzuziehen, sofern du nicht alleine in einem Raum bist.


Video laden
YouTube


Achtung: Parameter und Parameter im Vergleich

Aufgabe 2

Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 15-16) Notizblock mit Bleistift.

Parameter QF

a) Lies dir die Unterhaltung von Fabian, Merle und Lucio durch.

b) Denke dir zwei Funktionsterme quadratischer Funktionen aus für die gilt: (1) bzw. (2) . Gib jeweils die Werte für und an.

c) Zeichne die Parabeln zu deinen Funktionstermen aus b) in ein Koordinatensystem.

Dein Ergebnis kann zum Beispiel so aussehen:

Beispiel

Bei der Funktion sind .

Bei ist und .


Nutze das GeoGebra-Applet um deine eigene Lösung zu kontrollieren:

GeoGebra


Merksätze

Aufgabe 3

Lies dir die folgenden Merksätze aufmerksam durch.

Merke

Quadratische Funktionen können auf verschiedene Weisen in Termen dargestellt werden. Die beiden Formen, die du bisher kennengelernt hast, heißen

Eine Parabel kann immer in beiden Darstellungsformen beschrieben werden.

Merke
Durch Ausmultiplikation des Terms einer quadratischen Funktion in Scheitelpunktform erhält man den zugehörigen Term in Normalform.

Merke

Für den Parameter c gilt: Parameter QF


Übungen


Erstellt von: Elena Jedtke (Diskussion)

Abgerufen von „https://unterrichten.zum.de/index.php?title=Quadratische_Funktionen_erkunden/Von_der_Scheitelpunkt-_zur_Normalform&oldid=123396“