Quadratische Funktionen erkunden/Die Normalform: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
{{Box | {{Box | ||
|Aufgabe 1 | |Aufgabe 1 | ||
|'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 13) [[Datei:Notepad-117597.svg| | |'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 12-13) [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | ||
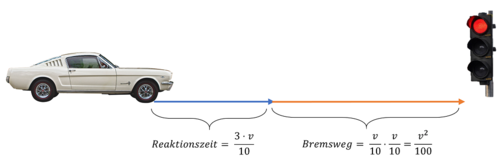
[[Datei:Anhalteweg.png|rahmenlos|zentriert|500px|Skizze Anhalteweg]] | [[Datei:Anhalteweg.png|rahmenlos|zentriert|500px|Skizze Anhalteweg]] | ||
In der [https://www.jungesportal.de/fuehrerschein/faustformeln-fuer-die-theorie.php Fahrschule] lernt man eine [https://de.wikipedia.org/wiki/Faustregel Faustformel] zur Berechnung des '''Bremsweges''' eines Autos kennen. Sie lautet „Geschwindigkeit durch 10 Mal Geschwindigkeit durch 10“ – in Termen ausgedrückt (mit v für Geschwindigkeit): | In der [https://www.jungesportal.de/fuehrerschein/faustformeln-fuer-die-theorie.php Fahrschule] lernt man eine [https://de.wikipedia.org/wiki/Faustregel Faustformel] zur Berechnung des '''Bremsweges''' eines Autos kennen. Sie lautet „Geschwindigkeit durch 10 Mal Geschwindigkeit durch 10“ – in Termen ausgedrückt (mit v für Geschwindigkeit): | ||
<math> f(v) \approx \frac{v}{10}\cdot\frac{v}{10} </math>. | |||
<math>f(v)\approx\frac{v}{10}\cdot\frac{v}{10}+\frac{3 \cdot v}{10}=\frac{v^2}{100}+\frac{3 \cdot v}{10}</math> | |||
Für den tatsächlichen Anhalteweg muss jedoch auch noch der '''Reaktionsweg''' des Fahrers beachtet werden. Durch ihn wird ein Weg von annähernd „drei Mal die Geschwindigkeit durch 10“ zurückgelegt und der zugehörige Term lautet: | |||
<math> f(v) \approx \frac{3 \cdot v}{10} </math>. | |||
Kombiniert man Bremsweg und Reaktionsweg, so lässt sich näherungsweies der '''Anhalteweg''' eines PKW bestimmen. Die zusammengesetzte Formel lautet: | |||
<math>f(v)\approx\frac{v}{10}\cdot\frac{v}{10}+\frac{3 \cdot v}{10}=\frac{v^2}{100}+\frac{3 \cdot v}{10}</math>. | |||
| Zeile 28: | Zeile 35: | ||
Zur Kontrolle kannst du das folgende Applet benutzen: | Zur Kontrolle kannst du das folgende Applet benutzen: | ||
{{LearningApp|app=ppixrfhoj17|width= | {{LearningApp|app=ppixrfhoj17|width=100%|height=250px}} | ||
{{Lösung versteckt|1=Der Anhalteweg wird durch einsetzen der Geschwindigkeiten v in die obige Formel berechnet. Es ergeben sich: | {{Lösung versteckt|1=Der Anhalteweg wird durch einsetzen der Geschwindigkeiten v in die obige Formel berechnet. Es ergeben sich: | ||
<math>f(30)\approx\frac{30}{10}\cdot\frac{30}{10}+\frac{3 \cdot 30}{10}=\frac{30^2}{100}+\frac{3 \cdot 30}{10}=18</math> | <math>f(30)\approx\frac{30}{10}\cdot\frac{30}{10}+\frac{3 \cdot 30}{10}=\frac{30^2}{100}+\frac{3 \cdot 30}{10}=18</math>, | ||
<math>f( | <math>f(50)\approx\frac{50^2}{100}+\frac{3 \cdot 50}{10}=40</math>, | ||
<math>f( | <math>f(70)\approx\frac{70^2}{100}+\frac{3 \cdot 70}{10}=70</math> und | ||
<math>f(100)\approx\frac{100^2}{100}+\frac{3 \cdot 100}{10}=130</math>. | |||
|2=Lösung anzeigen | |||
|3=Lösung verbergen}} | |||
'''b)''' Zeichne den zugehörigen Graphen in deinen Hefter und beschreibe seinen Verlauf in wenigen Sätzen. | '''b)''' Zeichne den zugehörigen Graphen in deinen Hefter und beschreibe seinen Verlauf in wenigen Sätzen. | ||
{{Lösung versteckt|1=Der Anhalteweg ist ''abhängig'' von der Geschwindigkeit. Trage deshalb die Geschwindigkeiten auf der x-Achse und die Anhaltewege auf der y-Achse deines Koordinatensystems ein.|2=Hilfe|3=Hilfe verstecken}} | {{Lösung versteckt|1=Der Anhalteweg ist ''abhängig'' von der Geschwindigkeit. Trage deshalb die Geschwindigkeiten auf der x-Achse und die Anhaltewege auf der y-Achse deines Koordinatensystems ein.|2=Hilfe anzeigen|3=Hilfe verstecken}} | ||
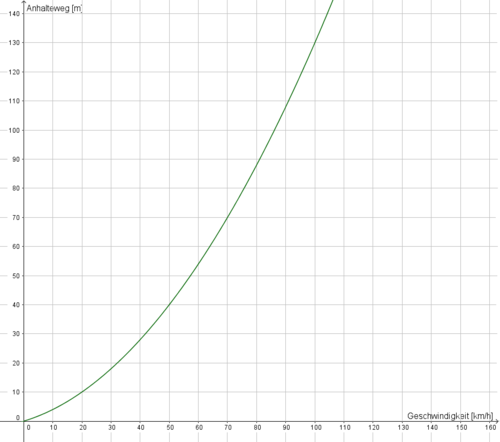
{{Lösung versteckt|1=[[Datei:Anhalteweg Graph.PNG|rahmenlos|500px|Anhalteweg eines PKW]] | {{Lösung versteckt|1=[[Datei:Anhalteweg Graph.PNG|rahmenlos|500px|Anhalteweg eines PKW]] | ||
Der Graph zeigt nur die positiven Werte der (quadratischen) Funktion für den Anhalteweg, da der Kontext keine sinnvolle Beschreibung negativer Werte erlaubt. Der Anhalteweg verlängert sich deutlich mit zunehmender Geschwindigkeit, das heißt der Graph steigt rasch an, was charakteristisch für quadratische Funktionen mit positivem Paramter a (hier a=1) ist.|2=Lösung|3=Lösung verstecken}} | Eine mögliche Beschreibung ist: | ||
Der Graph zeigt nur die positiven Werte der (quadratischen) Funktion für den Anhalteweg, da der Kontext keine sinnvolle Beschreibung negativer Werte erlaubt. Der Anhalteweg verlängert sich deutlich mit zunehmender Geschwindigkeit, das heißt der Graph steigt rasch an, was charakteristisch für quadratische Funktionen mit positivem Paramter <math>a</math> (hier <math>a=1</math>) ist.|2=Lösung anzeigen|3=Lösung verstecken}} | |||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
| Zeile 56: | Zeile 65: | ||
{{Box | {{Box | ||
|Aufgabe 2 | |Aufgabe 2 | ||
|'''Für diese Aufgabe benötigst du deinen Hefter ( | |'''Für diese Aufgabe benötigst du deinen Hefter (Merksätze, S. 5)''' [[Datei:Notepad-117597.svg|35px|Notizblock mit Bleistift|verweis=Datei:Notepad-117597.svg]]. | ||
'''a)''' Lies dir den folgenden Merksatz aufmerksam durch. | |||
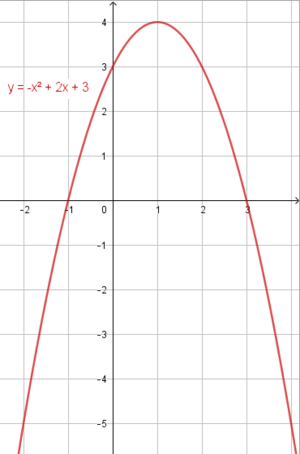
'''b)''' Als Beispiel ist bei dem Merksatz im Hefter der Funktionsterm <math>y=-x^2+2x+3</math> einer quadratischen Funktion in Normalform gegeben. Skizziere den zugehörigen Graphen in das Koordinatensystem. | |||
{{Lösung versteckt|1=Denke noch mal daran, was die Parameter <math>a, b</math> und <math>c</math> einzeln für eine Auswirkung auf die Lage des Graphen einer Funktion haben. Notiere deine Überlegungen. Kombiniert ergeben sie die Lage des Graphen der Funktion in Normalform.|2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
{{Lösung versteckt|1=[[Datei:NF Aufg2-Lösung.png|rahmenlos|300px|Lernpfade QF erkunden/erforschen, Kapitel NF]] | |||
< | Der Parameter <math>a=-1</math> ist kleiner als Null, weshalb die Parabel nach unten geöffnet ist. Da der Parameter genau den Wert <math>-1</math> annimmt, hat die Parabel die Form einer umgedrehten Normalparabel. | ||
Der Parameter <math>b=2</math> ist positiv und der Parameter <math>a</math> negativ, weshalb die Parabel nach rechts und oben verschoben wird. | |||
Der Parameter <math>c=3</math> gibt den y-Achsenabschnitt an.|2=Lösung anzeigen|3=Lösung verbergen}} | |||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
{{Box | {{Box | ||
|Merke | |Merke | ||
|Terme quadratischer Funktionen können in der Form '''<math>f(x)=ax^2+bx+c</math>''' (mit a | |Terme quadratischer Funktionen können in der Form '''<math>f(x)=ax^2+bx+c</math>''' (mit <math>a\neq0</math>) beschrieben werden. Diese Darstellungsform nennt man '''Normalform'''. In der Normalform quadratischer Funktionen kann der '''y-Achsenabschnitt <math>c</math>''' direkt abgelesen werden. | ||
|Merksatz | |Merksatz | ||
}} | }} | ||
| Zeile 77: | Zeile 94: | ||
'''a)''' Löse das folgende Quiz, indem du immer zwei Karten zu einem Paar zusammenfügst. | '''a)''' Löse das folgende Quiz, indem du immer zwei Karten zu einem Paar zusammenfügst. | ||
{{LearningApp|app=ps554x1ba17|width= | {{LearningApp|app=ps554x1ba17|width=100%|height=500px}} | ||
'''b)''' Du hattest noch ein paar Schwierigkeiten bei der Zuordnung? Schau dir die folgenden Tipps an und versuche es erneut! | '''b)''' Du hattest noch ein paar Schwierigkeiten bei der Zuordnung? Schau dir die folgenden Tipps an und versuche es erneut! | ||
{{Lösung versteckt|1=Du kannst... | |||
...den '''y-Achsenabschnitt''' an den Funktionsgraphen ablesen. Passt er zu einem der Funktionsterme? Oder findest du ihn in einer der Tabellen wieder? | |||
...'''einen beliebigen Punkt''' an den Graphen ablesen. Setze die Koordinaten in einen der Funktionsterme ein oder vergleiche sie mit den Werten in einer der Tabellen. | |||
...auf der [[{{BASEPAGENAME}}/Die Parameter der Scheitelpunktform|Parameterseite]] nachschauen wofür die Paramter in der Normalform stehen. Was ist nochmal der''' y-Achsenabschnitt''', was der '''Streckungsfaktor'''? | |||
{{Lösung versteckt|1=Der y-Achsenabschnitt hat die Koordinaten <math>P(0|c)</math>. In Tabellen findest du ihn deshalb als y-Wert zu <math>x=0</math>. In Termen steht er als Paramter <math>c</math>, z. B. mit <math>c=3</math> in <math>y=x^2+2x+3</math>.|2=Weitere Hilfe anzeigen|3=Weitere Hilfe verbergen}}|2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
{{Box | |||
|Aufgabe 4 | |||
'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 14) und einen Partner''' [[Datei:Notepad-117597.svg| | |'''Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 14) und einen Partner''' [[Datei:Notepad-117597.svg|32x32px]][[Datei:Puzzle-1020221_640.jpg|rahmenlos|80x80px]]. | ||
'''a)''' Finde Werte für a, b und c, so dass <math>f(x)</math> die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter | '''a)''' Finde Werte für a, b und c, so dass <math>f(x)</math> die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter. | ||
<ggb_applet id="YE3FKZgC" width="895" height="610" border="888888" /> | <ggb_applet id="YE3FKZgC" width="895" height="610" border="888888" /> | ||
{{Lösung versteckt|1=Überlege dir, welche Auswirkungen die einzelnen [[{{BASEPAGENAME}}/Die Parameter der Scheitelpunktform|Parameter]] auf die Lage der Parabel haben. | |||
* Ist die Parabel auf dem Bild nach oben oder nach unten geöffnet? Ist sie gestreckt oder gestaucht? Stell den Parameter a dementsprechend ein. | * Ist die Parabel auf dem Bild nach oben oder nach unten geöffnet? Ist sie gestreckt oder gestaucht? Stell den Parameter a dementsprechend ein. | ||
* In welchem [https://de.wikipedia.org/wiki/Quadrant Quadranten] liegt die Parabel? Muss b positiv oder negativ sein? | * In welchem [https://de.wikipedia.org/wiki/Quadrant Quadranten] liegt die Parabel? Muss b positiv oder negativ sein? | ||
* Kannst du einen y-Achsenabschnitt sehen? Stell den Parameter c dementsprechend ein. | * Kannst du einen y-Achsenabschnitt sehen? Stell den Parameter c dementsprechend ein. | ||
* Kannst du den y-Achsenabschnitt nicht erkennen? Stell die Paramter a und b so ein, dass die Parabel genau über oder unter der Parabel auf dem Foto ist. Danach kannst du sie mit dem Parameter c in die richtige Höhe verschieben.|2=Hilfe|3=Hilfe | |||
* Kannst du den y-Achsenabschnitt nicht erkennen? Stell die Paramter a und b so ein, dass die Parabel genau über oder unter der Parabel auf dem Foto ist. Danach kannst du sie mit dem Parameter c in die richtige Höhe verschieben.|2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben. | {{Lösung versteckt|1=Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben. | ||
{ | {{{!}} class="wikitable" | ||
{{!}}- | |||
! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter b !! Parameter c | ! Hintergrundbild!! Lösungsvorschlag !! Parameter a !! Parameter b !! Parameter c | ||
{{!}}- | |||
{{!}} Angry Birds {{!}}{{!}} <math>f(x)=-0.13x^2+1.82x-1.52</math> {{!}}{{!}} -0.14 ≤ a ≤ -0.13 {{!}}{{!}} 1.82 ≤ b ≤ 1.95 {{!}}{{!}} -1.85 ≤ c ≤ -1.52 | |||
{{!}}- | |||
{{!}} Golden Gate Bridge {{!}}{{!}} <math>f(x)=0.04x^2-0.46x+2.30</math> {{!}}{{!}} 0.03 ≤ a ≤ 0.05 {{!}}{{!}} -0.40 ≤ b ≤ -0.50 {{!}}{{!}} 2.05 ≤ c ≤ 2.30 | |||
{{!}}- | |||
{{!}} Springbrunnen {{!}}{{!}} <math>f(x)=-0.33x^2+3.20x-2.46</math> {{!}}{{!}} -0.40 ≤ a ≤ -0.30 {{!}}{{!}} 3.15 ≤ b ≤ 3.35 {{!}}{{!}} -2.95 ≤ c ≤ -2.45 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen links){{!}}{{!}} <math>f(x)=0.40x^2-2.00x+6.85</math> {{!}}{{!}} 0.33 ≤ a ≤ 0.47 {{!}}{{!}} 1.80 ≤ b ≤ 2.00 {{!}}{{!}} 6.35 ≤ c ≤ 6.85 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen mitte){{!}}{{!}} <math>f(x)=0.33x^2-3.86x+14.69</math> {{!}}{{!}} 0.30 ≤ a ≤ 0.36 {{!}}{{!}} -4.10 ≤ b ≤ -3.60 {{!}}{{!}} 13.65 ≤ c ≤ 14.95 | |||
{{!}}- | |||
{{!}} Elbphilharmonie (Bogen rechts){{!}}{{!}} <math>f(x)=0.22x^2-4.14x+23.04</math> {{!}}{{!}} 0.18 ≤ a ≤ 0.27 {{!}}{{!}} -3.40 ≤ b ≤ -5.05 {{!}}{{!}} 19.70 ≤ c ≤ 27.20 | |||
{{!}}- | |||
{{!}} Gebirgsformation {{!}}{{!}} <math>f(x)=-0.2x^2+2.16x-3.53</math> {{!}}{{!}} -0.30 ≤ a ≤ -0.15 {{!}}{{!}} 1.55 ≤ b ≤ 3.30 {{!}}{{!}} -6.35 ≤ c ≤ -1.70 | |||
{{!}}- | |||
{{!}} Motorrad-Stunt {{!}}{{!}} <math>f(x)=-0.07x^2+1.08x+1.79</math> {{!}}{{!}} -0.10 ≤ a ≤ -0.04 {{!}}{{!}} 0.85 ≤ b ≤ 1.30 {{!}}{{!}} 0.95 ≤ c ≤ 1.79 | |||
{{!}}- | |||
{{!}} Basketball {{!}}{{!}} <math>f(x)=-0.32x^2+4.16x-7.07</math> {{!}}{{!}} -0.35 ≤ a ≤ -0.29 {{!}}{{!}} 3.80 ≤ b ≤ 4.40 {{!}}{{!}} -7.40 ≤ c ≤ -6.10 | |||
|} | {{!}}} | ||
|2=Lösungsvorschläge anzeigen|3=Lösungsvorschläge verbergen}} | |||
'''b)''' Vielleicht ist dir aufgefallen, dass diese Aufgabe so ähnlich in dem Kapitel [[{{BASEPAGENAME}}/Die Scheitelpunktform|Scheitelpunktform]] auftaucht (S. 9). Vergleiche deine Ergebnisse aus beiden Aufgaben. Wo siehst du Parallelen und was ist anders? Notiere deine Überlegungen. | '''b)''' Vielleicht ist dir aufgefallen, dass diese Aufgabe so ähnlich in dem Kapitel [[{{BASEPAGENAME}}/Die Scheitelpunktform|Scheitelpunktform]] auftaucht (S. 9). Vergleiche deine Ergebnisse aus beiden Aufgaben. Wo siehst du Parallelen und was ist anders? Notiere deine Überlegungen. | ||
'''c)''' Vergleiche deine Erkenntnisse aus Aufgabe b) mit den Ergebnissen deines Partners. Fasst eure Erkenntnisse gemeinsam in wenigen Sätzen zusammen. | '''c)''' Vergleiche deine Erkenntnisse aus Aufgabe b) mit den Ergebnissen deines Partners. Fasst eure Erkenntnisse gemeinsam in wenigen Sätzen zusammen. | ||
{{Lösung versteckt|Es ist möglich, die gleiche Parabel mit einem Term in der Normalform und einem Term in der Scheitelpunktform quadratischer Funktionen zu beschreiben. Der Parameter a bleibt dabei in beiden Darstellungsformen gleich. Die Parameter b, c, d und e sind unterschiedlich.|Mögliche Beobachtungen anzeigen|Mögliche Beobachtungen verbergen}} | |||
{{Lösung versteckt|Es ist möglich, die gleiche Parabel mit einem Term in der Normalform und einem Term in der Scheitelpunktform quadratischer Funktionen zu beschreiben. Der Parameter a bleibt dabei in beiden Darstellungsformen gleich. Die Parameter b, c, d und e sind unterschiedlich.| | |Arbeitsmethode | ||
}} | |||
| Zeile 146: | Zeile 162: | ||
Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]]) | Erstellt von: [[Benutzer:Elena Jedtke|Elena Jedtke]] ([[Benutzer Diskussion:Elena Jedtke|Diskussion]]) | ||
[[Kategorie:Quadratische Funktion]] | [[Kategorie:Quadratische Funktion]] | ||
[[Kategorie:Interaktive Übung]] | [[Kategorie:Interaktive Übung]] | ||
[[Kategorie: | [[Kategorie:LearningApps]] | ||
[[Kategorie: | [[Kategorie:GeoGebra]] | ||
Aktuelle Version vom 30. März 2022, 21:38 Uhr
In diesem Kapitel wirst du Experte für die Normalform quadratischer Funktionen. Bisher hast du quadratische Funktionen in der Scheitelpunktform kennengelernt. In Anwendungen wird jedoch häufig diese andere Variante quadratischer Funktionen genutzt. In diesem Kapitel
- lernst du eine Anwendungsbeispiel aus der Fahrschule kennen,
- erfährst, wie Terme quadratischer Funktionen in Normalform aussehen und
- du lernst in einem Quiz und einer Partnerarbeit Eigenschaften und Besonderheiten der Normalform näher kennen.
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 12-13) ![]() .
.
In der Fahrschule lernt man eine Faustformel zur Berechnung des Bremsweges eines Autos kennen. Sie lautet „Geschwindigkeit durch 10 Mal Geschwindigkeit durch 10“ – in Termen ausgedrückt (mit v für Geschwindigkeit):
.
Für den tatsächlichen Anhalteweg muss jedoch auch noch der Reaktionsweg des Fahrers beachtet werden. Durch ihn wird ein Weg von annähernd „drei Mal die Geschwindigkeit durch 10“ zurückgelegt und der zugehörige Term lautet:
.
Kombiniert man Bremsweg und Reaktionsweg, so lässt sich näherungsweies der Anhalteweg eines PKW bestimmen. Die zusammengesetzte Formel lautet:
.
a) Berechne den Anhalteweg für die Geschwindigkeiten: 30 km/h, 50 km/h und 70 km/h und 100 km/h. Trage deine Ergebnisse in die Tabelle in deinem Hefter ein.
Zur Kontrolle kannst du das folgende Applet benutzen:
Der Anhalteweg wird durch einsetzen der Geschwindigkeiten v in die obige Formel berechnet. Es ergeben sich: ,
,
und
.b) Zeichne den zugehörigen Graphen in deinen Hefter und beschreibe seinen Verlauf in wenigen Sätzen.
Eine mögliche Beschreibung ist:
Für diese Aufgabe benötigst du deinen Hefter (Merksätze, S. 5) ![]() .
.
a) Lies dir den folgenden Merksatz aufmerksam durch.
b) Als Beispiel ist bei dem Merksatz im Hefter der Funktionsterm einer quadratischen Funktion in Normalform gegeben. Skizziere den zugehörigen Graphen in das Koordinatensystem.
Der Parameter ist kleiner als Null, weshalb die Parabel nach unten geöffnet ist. Da der Parameter genau den Wert annimmt, hat die Parabel die Form einer umgedrehten Normalparabel.
Der Parameter ist positiv und der Parameter negativ, weshalb die Parabel nach rechts und oben verschoben wird.
Der Parameter gibt den y-Achsenabschnitt an.Terme quadratischer Funktionen können in der Form (mit ) beschrieben werden. Diese Darstellungsform nennt man Normalform. In der Normalform quadratischer Funktionen kann der y-Achsenabschnitt direkt abgelesen werden.
Das folgende Quiz beschäftigt sich mit dem Wechsel zwischen verschiedenen Darstellungsarten (Funktionsterm, Graph und Tabelle) quadratischer Funktionen.
a) Löse das folgende Quiz, indem du immer zwei Karten zu einem Paar zusammenfügst.
b) Du hattest noch ein paar Schwierigkeiten bei der Zuordnung? Schau dir die folgenden Tipps an und versuche es erneut!
Du kannst...
...den y-Achsenabschnitt an den Funktionsgraphen ablesen. Passt er zu einem der Funktionsterme? Oder findest du ihn in einer der Tabellen wieder?
...einen beliebigen Punkt an den Graphen ablesen. Setze die Koordinaten in einen der Funktionsterme ein oder vergleiche sie mit den Werten in einer der Tabellen.
...auf der Parameterseite nachschauen wofür die Paramter in der Normalform stehen. Was ist nochmal der y-Achsenabschnitt, was der Streckungsfaktor?
Für diese Aufgabe benötigst du deinen Hefter (Lernpfadaufgaben, S. 14) und einen Partner ![]()
 .
.
a) Finde Werte für a, b und c, so dass die Kurve auf dem Bild möglichst gut beschreibt. Entscheide dich für drei Hintergrundbilder deiner Wahl und notiere den Funktionsterm in deinem Hefter.

Überlege dir, welche Auswirkungen die einzelnen Parameter auf die Lage der Parabel haben.
- Ist die Parabel auf dem Bild nach oben oder nach unten geöffnet? Ist sie gestreckt oder gestaucht? Stell den Parameter a dementsprechend ein.
- In welchem Quadranten liegt die Parabel? Muss b positiv oder negativ sein?
- Kannst du einen y-Achsenabschnitt sehen? Stell den Parameter c dementsprechend ein.
- Kannst du den y-Achsenabschnitt nicht erkennen? Stell die Paramter a und b so ein, dass die Parabel genau über oder unter der Parabel auf dem Foto ist. Danach kannst du sie mit dem Parameter c in die richtige Höhe verschieben.
Da es nicht die eine richtige Lösung gibt, findest du in der Tabelle Lösungsvorschläge sowie Spielräume, in denen die Parameter liegen können, um den Verlauf angemessen zu beschreiben.
| Hintergrundbild | Lösungsvorschlag | Parameter a | Parameter b | Parameter c |
|---|---|---|---|---|
| Angry Birds | -0.14 ≤ a ≤ -0.13 | 1.82 ≤ b ≤ 1.95 | -1.85 ≤ c ≤ -1.52 | |
| Golden Gate Bridge | 0.03 ≤ a ≤ 0.05 | -0.40 ≤ b ≤ -0.50 | 2.05 ≤ c ≤ 2.30 | |
| Springbrunnen | -0.40 ≤ a ≤ -0.30 | 3.15 ≤ b ≤ 3.35 | -2.95 ≤ c ≤ -2.45 | |
| Elbphilharmonie (Bogen links) | 0.33 ≤ a ≤ 0.47 | 1.80 ≤ b ≤ 2.00 | 6.35 ≤ c ≤ 6.85 | |
| Elbphilharmonie (Bogen mitte) | 0.30 ≤ a ≤ 0.36 | -4.10 ≤ b ≤ -3.60 | 13.65 ≤ c ≤ 14.95 | |
| Elbphilharmonie (Bogen rechts) | 0.18 ≤ a ≤ 0.27 | -3.40 ≤ b ≤ -5.05 | 19.70 ≤ c ≤ 27.20 | |
| Gebirgsformation | -0.30 ≤ a ≤ -0.15 | 1.55 ≤ b ≤ 3.30 | -6.35 ≤ c ≤ -1.70 | |
| Motorrad-Stunt | -0.10 ≤ a ≤ -0.04 | 0.85 ≤ b ≤ 1.30 | 0.95 ≤ c ≤ 1.79 | |
| Basketball | -0.35 ≤ a ≤ -0.29 | 3.80 ≤ b ≤ 4.40 | -7.40 ≤ c ≤ -6.10 |
b) Vielleicht ist dir aufgefallen, dass diese Aufgabe so ähnlich in dem Kapitel Scheitelpunktform auftaucht (S. 9). Vergleiche deine Ergebnisse aus beiden Aufgaben. Wo siehst du Parallelen und was ist anders? Notiere deine Überlegungen.
c) Vergleiche deine Erkenntnisse aus Aufgabe b) mit den Ergebnissen deines Partners. Fasst eure Erkenntnisse gemeinsam in wenigen Sätzen zusammen.
Erstellt von: Elena Jedtke (Diskussion)