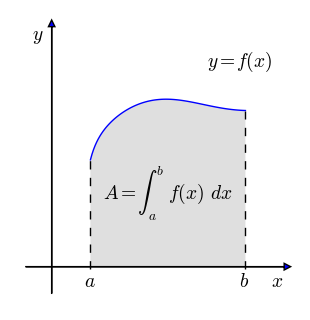
Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Integralrechnung/Aufgaben II: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Dickesen Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (33 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Aufgaben II== | {{Navigation verstecken|{{Lernpfad Integral}}}} | ||
{{ | <!--==Aufgaben II==--> | ||
===Beispiel=== | |||
Das Integral <math>\int\limits_1^4 x^2 \ \mathrm{d}x</math> berechnet sich mit Hilfe des Hauptsatzes der Differential- und Integralrechnung wie folgt: | |||
<br><br> | |||
<math>\int\limits_1^4 x^2 \ \mathrm{d}x = \left[ \frac{1}{3} x^3 \right]_1^4 = \frac{1}{3} \cdot 4^3 - \frac{1}{3} \cdot 1^3 = \frac{64}{3} - \frac{1}{3} = 21</math>. | |||
<br><br> | |||
{{Box|1=Aufgabe 17|2= | |||
Berechne das bestimmte Integral! | Berechne das bestimmte Integral! | ||
# <math>\int\limits_2^5 \frac{2}{3}x \ \mathrm{d}x; \qquad \int\limits_1^3 \sqrt{5} \ \mathrm{d}x; | # <math>\int\limits_2^5 \frac{2}{3}x \ \mathrm{d}x; \qquad \int\limits_1^3 \sqrt{5} \ \mathrm{d}x; | ||
| Zeile 6: | Zeile 12: | ||
# <math>\int\limits_3^7 2 \ \mathrm{d}x; \qquad \int\limits_2^5 1 \ \mathrm{d}x; | # <math>\int\limits_3^7 2 \ \mathrm{d}x; \qquad \int\limits_2^5 1 \ \mathrm{d}x; | ||
\qquad \int\limits_2^4 0 \ \mathrm{d}x</math> | \qquad \int\limits_2^4 0 \ \mathrm{d}x</math> | ||
# <math>\int\limits_3^8 \frac{1}{\sqrt{x}}x \ \mathrm{d}x; \qquad \int\limits_1^2 \frac{5}{\sqrt{x}} \ \mathrm{d}x; \qquad \int\ | # <math>\int\limits_3^8 \frac{1}{\sqrt{x}}x \ \mathrm{d}x; \qquad \int\limits_1^2 \frac{5}{\sqrt{x}} \ \mathrm{d}x; \qquad \int\limits_4^9 \frac{1}{2 \cdot \sqrt{x}} \ \mathrm{d}x</math> | ||
|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= | |||
# <math>7; \quad 2 \sqrt{5}; \quad \frac{122}{3}</math> | |||
# <math>8; \quad 3; \quad 0</math> | |||
# <math>11,62; \quad 10 \sqrt{2} - 10; \quad 1</math> | |||
}} | }} | ||
<br> | <br> | ||
{{Lösung versteckt|{{Lösung| | {{Box|1=Aufgabe 18|2= | ||
# <math> | Berechne das Integral. | ||
}} | # <math>\int\limits_0^3 (2x^3 + 3x - 2) \ \mathrm{d}x</math> | ||
# <math>\int\limits_1^2 \frac{1 + 3x^2}{5} \ \mathrm{d}x</math> | |||
# <math>\int\limits_1^3 \frac{3x^2 - 7\sqrt{x}}{x} \ \mathrm{d}x</math> | |||
|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= | |||
# <math>48</math> | |||
# <math>\frac{8}{5}</math> | |||
# <math>26 - 14 \sqrt{3}</math> | |||
}} | |||
<br> | |||
{{Box|1=Aufgabe 19|2= | |||
Berechne die Fläche zwischen dem Graphen von <math>f</math> und der x-Achse. | |||
# <math>f(x) = -x^3 + x</math> | |||
# <math>f(x) = 4 x^2 - 3</math> | |||
# <math>f(x) = (x^2 - 16)(x^2 + 3)</math> | |||
|3=Arbeitsmethode}} | |||
{{Lösung versteckt|1= | |||
# Es ergeben sich die Nullstellen -1, 0 und 1. Damit müssen zwei Integrale ausgewertet werden. Diese erstrecken sich von der ersten bis zur zweiten Nullstelle sowie von der zweiten bis zur dritten. Insgesamt ergibt sich der Wert für die Fläche aus den Beträgen der einzelnen Integrale zu <math>\frac{1}{2}</math>. Nach der Regel zur Intervalladditivität könnte auch ein einzelnes Integral von der niedrigsten bis zur höchsten Nullstelle betrachtet werden, wenn nach dem Wert des Integrals gefragt wäre. Jedoch ist nach der Fläche gefragt. Deshalb müssen die Beträge der Integrale einzeln betrachtet werden!!! Vergleiche dazu den Wert des Integrals in denselben Grenzen, er ist 0. | |||
# Nullstellen: <math>\frac{1}{2}\sqrt{3}</math> und <math>- \frac{1}{2}\sqrt{3}</math>. Der Flächeninhalt hat den Wert <math>2 \sqrt{3}</math>. | |||
# Nullstellen: 4 und -4. Der Flächeninhalt hat den Wert <math>\frac{7936}{15}</math>. | |||
<br> | <br> | ||
Bemerkung: Hier gibt es nur positive Ergebnisse, da die Beträge der Integrale auszuwerten sind, denn es waren ja die Flächen gefragt und nicht die Integrale! | |||
}} | }} | ||
[[Kategorie:Integralrechnung]] | |||
Aktuelle Version vom 23. April 2022, 16:46 Uhr
Beispiel
Das Integral berechnet sich mit Hilfe des Hauptsatzes der Differential- und Integralrechnung wie folgt:
.
Aufgabe 17
Berechne das bestimmte Integral!
Aufgabe 18
Berechne das Integral.
Aufgabe 19
Berechne die Fläche zwischen dem Graphen von und der x-Achse.
- Es ergeben sich die Nullstellen -1, 0 und 1. Damit müssen zwei Integrale ausgewertet werden. Diese erstrecken sich von der ersten bis zur zweiten Nullstelle sowie von der zweiten bis zur dritten. Insgesamt ergibt sich der Wert für die Fläche aus den Beträgen der einzelnen Integrale zu . Nach der Regel zur Intervalladditivität könnte auch ein einzelnes Integral von der niedrigsten bis zur höchsten Nullstelle betrachtet werden, wenn nach dem Wert des Integrals gefragt wäre. Jedoch ist nach der Fläche gefragt. Deshalb müssen die Beträge der Integrale einzeln betrachtet werden!!! Vergleiche dazu den Wert des Integrals in denselben Grenzen, er ist 0.
- Nullstellen: und . Der Flächeninhalt hat den Wert .
- Nullstellen: 4 und -4. Der Flächeninhalt hat den Wert .