Integralrechnung/Hauptsatz: Unterschied zwischen den Versionen
Main>BirgitLachner Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (10 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=Hauptsatz der Differential- und Integralrechnung= | {{Navigation verstecken|{{Lernpfad Integral}}}} | ||
==Hauptsatz der Differential- und Integralrechnung== | |||
Bevor wir den Hauptsatz der Differential- und Integralrechnung aufschreiben, fassen wir noch einmal kurz die dafür wichtigsten Erkenntnisse zusammen. | Bevor wir den Hauptsatz der Differential- und Integralrechnung aufschreiben, fassen wir noch einmal kurz die dafür wichtigsten Erkenntnisse zusammen. | ||
{{ | {{Box|1=Zusammenfassung|2= | ||
* Das '''bestimmte Integral''' der Funktion <math>f(x)</math> ist gleich der Summe der orientierten (mit Vorzeichen versehenen) Flächeninhalte zwischen dem Graphen von <math>f(x)</math> und der x-Achse in den angegebenen Grenzen <math>a</math> und <math>b</math>. | * Das '''bestimmte Integral''' der Funktion <math>f(x)</math> ist gleich der Summe der orientierten (mit Vorzeichen versehenen) Flächeninhalte zwischen dem Graphen von <math>f(x)</math> und der x-Achse in den angegebenen Grenzen <math>a</math> und <math>b</math>. | ||
* Die "Flächeninhaltsfunktion" <math>F(x)</math> beschreibt den (orientierten) Flächeninhalt zwischen dem Graphen von <math>f(x)</math> und der x-Achse. | * Die "Flächeninhaltsfunktion" <math>F(x)</math> beschreibt den (orientierten) Flächeninhalt zwischen dem Graphen von <math>f(x)</math> und der x-Achse. | ||
| Zeile 21: | Zeile 19: | ||
</div> | </div> | ||
* Wenn <math>F(x)</math> eine Stammfunktion von <math>f(x)</math> ist, dann ist <math>F(x) + c</math> mit <math>c \in \mathbb{R}</math> ebenfalls eine Stammfunktion von <math>f(x)</math>. | * Wenn <math>F(x)</math> eine Stammfunktion von <math>f(x)</math> ist, dann ist <math>F(x) + c</math> mit <math>c \in \mathbb{R}</math> ebenfalls eine Stammfunktion von <math>f(x)</math>. | ||
| | |3=Unterrichtsidee }} | ||
}} | |||
<br><br> | <br><br> | ||
Wenn man die Punkte in der Zusammenfassung oben richtig kombiniert, dann erhält man den Hauptsatz der Differential- und Integralrechnung: | Wenn man die Punkte in der Zusammenfassung oben richtig kombiniert, dann erhält man den Hauptsatz der Differential- und Integralrechnung: | ||
<br> | <br> | ||
{{ | {{Box|1=Hauptsatz der Differential- und Integralrechnung|2= | ||
a) Sei <math>f</math> eine stetige (mit durchgehendem Graphen) Funktion mit reellen Funktionswerten. Dann gilt mit jeder konstanten Zahl <math>x_0 \in [a;b]</math>: | a) Sei <math>f</math> eine stetige (mit durchgehendem Graphen) Funktion mit reellen Funktionswerten. Dann gilt mit jeder konstanten Zahl <math>x_0 \in [a;b]</math>: | ||
<div align="center"> | <div align="center"> | ||
| Zeile 43: | Zeile 34: | ||
<math>\int \limits_a^b f(x) \ \mathrm{d}x = \left[ F(x) \right]^b_a = F(b) - F(a)</math> | <math>\int \limits_a^b f(x) \ \mathrm{d}x = \left[ F(x) \right]^b_a = F(b) - F(a)</math> | ||
</div> | </div> | ||
| | |3=Merksatz}} | ||
}} | |||
<br> | <br> | ||
Im ersten Teil des Hauptsatzes (oder auch ''Fundamentalsatz der Analysis'' genannt) steht unter dem Integral das Differential d<math>t</math> und der Integrand <math>f(t)</math>. Dies hat folgenden Grund: <br> | Im ersten Teil des Hauptsatzes (oder auch ''Fundamentalsatz der Analysis'' genannt) steht unter dem Integral das Differential d<math>t</math> und der Integrand <math>f(t)</math>. Dies hat folgenden Grund: <br> | ||
Die obere Grenze des Integrals ist die Variable <math>x</math>. Wenn nun das Differential und die Funktion ebenfalls in x variabel wären, dann könnte man die beiden Variablen nicht mehr voneinander unterscheiden! Jedoch müssen sie unterschieden werden, da sie ja i.A. verschiedene Werte annehmen, vgl. dazu auch die Definition des bestimmten Integrals. Dort ist die obere Grenze durch die feste Zahl <math>b</math> gegeben während die Integrationsvariable <math>x</math> ist. Zwar durchläuft <math>x</math> das ganze Intervall <math>[a;b]</math>, jedoch sind seine Werte doch i.A. von <math>b</math> verschieden. Erst am Ende des Intervalls sind beide gleich! <br> | Die obere Grenze des Integrals ist die Variable <math>x</math>. Wenn nun das Differential und die Funktion ebenfalls in x variabel wären, dann könnte man die beiden Variablen nicht mehr voneinander unterscheiden! Jedoch müssen sie unterschieden werden, da sie ja i.A. verschiedene Werte annehmen, vgl. dazu auch die Definition des bestimmten Integrals. Dort ist die obere Grenze durch die feste Zahl <math>b</math> gegeben während die Integrationsvariable <math>x</math> ist. Zwar durchläuft <math>x</math> das ganze Intervall <math>[a;b]</math>, jedoch sind seine Werte doch i.A. von <math>b</math> verschieden. Erst am Ende des Intervalls sind beide gleich! <br> | ||
Das Umbenennen der Integrationsvariable stellt lediglich eine formale Änderung dar und ist jederzeit erlaubt, wenn auch die Variable des Integranden geändert wird. So z.B. gilt für jedes bestimmte Integral einer Funktion <math>f</math>: | Das Umbenennen der Integrationsvariable stellt lediglich eine formale Änderung dar und ist jederzeit erlaubt, wenn auch die Variable des Integranden geändert wird. So z.B. gilt für jedes bestimmte Integral einer Funktion <math>f</math>: | ||
<div align="center> | <div align="center"> | ||
<math>\int \limits_a^b f(x) \ \mathrm{d}x = \int \limits_a^b f(t) \ \mathrm{d}t = \int \limits_a^b f(s) \ \mathrm{d}s = \int \limits_a^b f(\varphi) \ \mathrm{d}\varphi = \dots</math> | <math>\int \limits_a^b f(x) \ \mathrm{d}x = \int \limits_a^b f(t) \ \mathrm{d}t = \int \limits_a^b f(s) \ \mathrm{d}s = \int \limits_a^b f(\varphi) \ \mathrm{d}\varphi = \dots</math> | ||
</div> | </div> | ||
<br> | <br> | ||
==Beweis des Hauptsatzes== | ==Beweis des Hauptsatzes== | ||
Der Beweis des Hauptsatzes der Differential- und Integralrechnung ist keine Pflicht für den Grundkurs, jedoch gebe ich hier einen Link zu einem sehr anschaulichen [http://teacher.eduhi.at/alindner/Dyn_Geometrie/DiffInt/HS_DiffInt.htm Beweis | Der Beweis des Hauptsatzes der Differential- und Integralrechnung ist keine Pflicht für den Grundkurs, jedoch gebe ich hier einen Link zu einem sehr anschaulichen [http://teacher.eduhi.at/alindner/Dyn_Geometrie/DiffInt/HS_DiffInt.htm '''Beweis mit Geogebra'''] . | ||
{{Fortsetzung|weiter=Integrationsregeln|weiterlink=Integral/Integrationsregeln}} | |||
[[Kategorie:Integralrechnung]] | [[Kategorie:Integralrechnung]] | ||
Aktuelle Version vom 23. April 2022, 16:45 Uhr
Hauptsatz der Differential- und Integralrechnung
Bevor wir den Hauptsatz der Differential- und Integralrechnung aufschreiben, fassen wir noch einmal kurz die dafür wichtigsten Erkenntnisse zusammen.
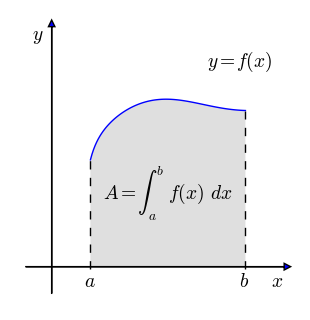
- Das bestimmte Integral der Funktion ist gleich der Summe der orientierten (mit Vorzeichen versehenen) Flächeninhalte zwischen dem Graphen von und der x-Achse in den angegebenen Grenzen und .
- Die "Flächeninhaltsfunktion" beschreibt den (orientierten) Flächeninhalt zwischen dem Graphen von und der x-Achse.
- Der Zusammenhang zwischen dem bestimmten Integral von und der Flächeninhaltsfunktion ist folgender:
.
- Die "Flächeninhaltsfunktion" wird Stammfunktion genannt (da sie mehr als nur den Flächeninhalt angibt, vgl. spätere Anwendungen!) und sie besitzt folgenden Zusammenhang mit :
- Integrieren oder das Auffinden einer Stammfunktion oder Bildung des unbestimmten Integrals bedeutet die Umkehrung zum Differenzieren. Das unbestimmte Integral ist gleich der Stammfunktion:
- Wenn eine Stammfunktion von ist, dann ist mit ebenfalls eine Stammfunktion von .
Wenn man die Punkte in der Zusammenfassung oben richtig kombiniert, dann erhält man den Hauptsatz der Differential- und Integralrechnung:
a) Sei eine stetige (mit durchgehendem Graphen) Funktion mit reellen Funktionswerten. Dann gilt mit jeder konstanten Zahl :
- Dabei ist eine Stammfunktion zu und es gilt: .
b) Sei eine stetige reellwertige Funktion mit Stammfunktion . Dann gilt:
Im ersten Teil des Hauptsatzes (oder auch Fundamentalsatz der Analysis genannt) steht unter dem Integral das Differential d und der Integrand . Dies hat folgenden Grund:
Die obere Grenze des Integrals ist die Variable . Wenn nun das Differential und die Funktion ebenfalls in x variabel wären, dann könnte man die beiden Variablen nicht mehr voneinander unterscheiden! Jedoch müssen sie unterschieden werden, da sie ja i.A. verschiedene Werte annehmen, vgl. dazu auch die Definition des bestimmten Integrals. Dort ist die obere Grenze durch die feste Zahl gegeben während die Integrationsvariable ist. Zwar durchläuft das ganze Intervall , jedoch sind seine Werte doch i.A. von verschieden. Erst am Ende des Intervalls sind beide gleich!
Das Umbenennen der Integrationsvariable stellt lediglich eine formale Änderung dar und ist jederzeit erlaubt, wenn auch die Variable des Integranden geändert wird. So z.B. gilt für jedes bestimmte Integral einer Funktion :
Beweis des Hauptsatzes
Der Beweis des Hauptsatzes der Differential- und Integralrechnung ist keine Pflicht für den Grundkurs, jedoch gebe ich hier einen Link zu einem sehr anschaulichen Beweis mit Geogebra .