Lernpfad Energie/Energieumwandlung und Wirkungsgrad: Unterschied zwischen den Versionen
Main>Karl Kirst K (Navigation nach unten) |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (19 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== | ==Reibung - ein "Energie-Leck"== | ||
Würde man unser Beispiel ernst nehmen, müsste unser Skater nur rechts oben starten und könnte dann im Grunde stundenlang hin- und herfahren, ohne sich anzustrengen. Ständig würde potentielle Energie in kinetische Energie umgewandelt und umgekehrt. Es ist klar: in der Wirklichkeit funktioniert das so nicht. | Würde man unser Beispiel ernst nehmen, müsste unser Skater nur rechts oben starten und könnte dann im Grunde stundenlang hin- und herfahren, ohne sich anzustrengen. Ständig würde potentielle Energie in kinetische Energie umgewandelt und umgekehrt. Es ist klar: in der Wirklichkeit funktioniert das so nicht. Ein Skater, der einfach nur auf dem Skateboard hin- und her rollt, wird mit der Zeit immer geringere Höhen an den höchsten Punkten erreichen. Auch wird er im tiefsten Punkt immer langsamer rollen. | ||
Was ist dann aber mit unserem "Glaubenssatz" von der Energieerhaltung, der sich unserem Beispiel mit den Wassergläsern so ausgedrückt hatte, dass beim "Umschütten" von einem Glas ins andere keine Flüssigkeit verloren geht. Ist dieser "Glaubenssatz" jetzt einfach falsch - oder können wir ihn noch "retten". | |||
Was auf jeden Fall nicht mehr funktioniert ist das Bild mit nur zwei Wassergläsern und der immer gleichen Menge Flüssigkeit, die sich irgendwie auf die beiden Gläser verteilt. | |||
[[Bild:LE_3 Pot_Kin.png|350px]] | |||
Spätestens dann, wenn der Skater wegen der Reibung praktisch zur Ruhe gekommen ist, wären die beiden Gläser in unserem Bild leer; die Flüssigkeit hätte im Laufe der Zeit irgendwie verloren gehen müssen (sozusagen verschüttet worden sein). | |||
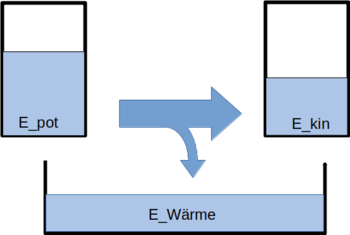
Wir können das Bild aber retten, indem wir einen weiteren Behälter für unsere erfinden, in dem wir die (verloren geglaubte oder verschüttete) "Energieflüssigkeit" auffangen. | |||
[[Bild:LE_3 Pot_Kin_Waerme.png|350px]] | |||
{{ | {{Box | ||
|Aufgabe 4.1 Der Energieerhaltungssatz mit Reibung | |||
| | |||
Der Energieerhaltungssatz gilt also noch immer. Allerdings kommt nun die Energieform der Wärme hinzu. Formuliere den Energieerhaltungssatz nun unter Berücksichtigung von Reibung in Deinem Lerntagebuch als Formel für die Punkte A, B und C. Wir nehmen an, dass alle Energie, die durch Reibung umgewandelt wird, an Ende zu einer Energieform beiträgt, die man Wärmeenergie E<sub>Wärme</sub> nennt. | Der Energieerhaltungssatz gilt also noch immer. Allerdings kommt nun die Energieform der Wärme hinzu. Formuliere den Energieerhaltungssatz nun unter Berücksichtigung von Reibung in Deinem Lerntagebuch als Formel für die Punkte A, B und C. Wir nehmen an, dass alle Energie, die durch Reibung umgewandelt wird, an Ende zu einer Energieform beiträgt, die man Wärmeenergie E<sub>Wärme</sub> nennt. | ||
|Arbeitsmethode | |||
}} | }} | ||
| Zeile 44: | Zeile 33: | ||
Wenn sich unser Skater an den oberen Rand der Halfpipe stellt und sich losrollen lässt, so verfolgt er damit ein bestimmtes Ziel: Er will schneller werden. Durch die Reibung wird er allerdings nicht ganz so viel schneller, wie er es sich vielleicht wünscht. Wie stark die Reibung ist, hängt dabei von vielen Einflüssen ab; vor allem aber auch von den Lagern seines Skateboards und von der Oberfläche Halfpipe. Wir können davon ausgehen, dass durch Reibung letztlich Energie in Wärmeenergie umgewandelt wird. Das kann auch über Umwege passieren: ein Skateboard rollt nicht lautlos und auch der Schall trägt Energie weg. Diese wird dann irgendwo in der Umgebung wieder durch Reibung ebenfalls in Wärme umgewandelt. Die Wärmeenergie ist im Falle unseres Skaters ein unerwünschtes "Abfallprodukt". | Wenn sich unser Skater an den oberen Rand der Halfpipe stellt und sich losrollen lässt, so verfolgt er damit ein bestimmtes Ziel: Er will schneller werden. Durch die Reibung wird er allerdings nicht ganz so viel schneller, wie er es sich vielleicht wünscht. Wie stark die Reibung ist, hängt dabei von vielen Einflüssen ab; vor allem aber auch von den Lagern seines Skateboards und von der Oberfläche Halfpipe. Wir können davon ausgehen, dass durch Reibung letztlich Energie in Wärmeenergie umgewandelt wird. Das kann auch über Umwege passieren: ein Skateboard rollt nicht lautlos und auch der Schall trägt Energie weg. Diese wird dann irgendwo in der Umgebung wieder durch Reibung ebenfalls in Wärme umgewandelt. Die Wärmeenergie ist im Falle unseres Skaters ein unerwünschtes "Abfallprodukt". | ||
{{ | {{Box | ||
|Aufgabe 4.2 Aufteilung in "nützlich" und "nutzlos" beschreiben | |||
| | |||
Wir betrachten nochmal den Fall, dass unser Skater aus einer Höhe von 2,5 Meter in der Halfpipe nach unten fährt. | Wir betrachten nochmal den Fall, dass unser Skater aus einer Höhe von 2,5 Meter in der Halfpipe nach unten fährt. | ||
[[Bild:LE3 halfpipe mit Buchstaben und Höhen2.jpg|350px]]<br> | [[Bild:LE3 halfpipe mit Buchstaben und Höhen2.jpg|350px]]<br> | ||
| Zeile 51: | Zeile 41: | ||
a) Nenne die Energieformen, in die die Lageenergie umgewandelt wird.<br> | a) Nenne die Energieformen, in die die Lageenergie umgewandelt wird.<br> | ||
b) Berechne, wie viel der ursprünglich als Lageenergie gespeicherten Energie bei Erreichen von Punkt B als zusätzliche Wärmeenergie vorliegt.<br> | b) Berechne, wie viel der ursprünglich als Lageenergie gespeicherten Energie bei Erreichen von Punkt B als zusätzliche Wärmeenergie vorliegt.<br> | ||
{{Lösung versteckt| | |||
Trotz Reibung bleibt die Gesamtenergie, also die Summe von Lageenergie, Bewegungsenergie und in diesem Fall Wärmeenergie, erhalten. Die Lageenergie und die Bewegungsenergie kann man sowohl am Startpunkt als auch in Punkt B leicht errechnen. Die Differenz an Wärmeenergie <br><math>E_\text{Wärme,B}-E_\text{Wärme,Start}</math><br> kann man so leicht ausrechnen. | Trotz Reibung bleibt die Gesamtenergie, also die Summe von Lageenergie, Bewegungsenergie und in diesem Fall Wärmeenergie, erhalten. Die Lageenergie und die Bewegungsenergie kann man sowohl am Startpunkt als auch in Punkt B leicht errechnen. Die Differenz an Wärmeenergie <br><math>E_\text{Wärme,B}-E_\text{Wärme,Start}</math><br> kann man so leicht ausrechnen. | ||
|Tipp anzeigen|Tipp verbergen | |||
}}<br> | }}<br> | ||
c) Berechne das Verhältnis von Bewegungsenergie am Punkt B zur Lageenergie beim Start. <br> | c) Berechne das Verhältnis von Bewegungsenergie am Punkt B zur Lageenergie beim Start. <br> | ||
d) Beschreibe, was kannst Du über die physikalische Einheit dieses Verhältnisses sagen kannst? | d) Beschreibe, was kannst Du über die physikalische Einheit dieses Verhältnisses sagen kannst? | ||
|Arbeitsmethode | |||
}} | }} | ||
| Zeile 64: | Zeile 55: | ||
[[Bild:Wirkungsgrad-Bild2.jpg|400px]] | [[Bild:Wirkungsgrad-Bild2.jpg|400px]] | ||
<math> | <math> | ||
| Zeile 74: | Zeile 64: | ||
== Wirkungsgrad im Alltag == | == Wirkungsgrad im Alltag == | ||
{{ | {{Box | ||
|Aufgabe 4.3 Wirkungsgrad von Leuchtmitteln | |||
| | |||
[[Datei:New torch bulb.jpg|miniatur|LED- und Glühlampe]] | [[Datei:New torch bulb.jpg|miniatur|LED- und Glühlampe]] | ||
Eine 12W-Glühlampe wandelt innerhalb einer Sekunde 12 Joule elektrischer Energie in Lichtenergie um. Naja, jedenfalls teilweise. Denn der typische Wert einer Glühlampe liegt bei etwa 5 Prozent. <br> | Eine 12W-Glühlampe wandelt innerhalb einer Sekunde 12 Joule elektrischer Energie in Lichtenergie um. Naja, jedenfalls teilweise. Denn der typische Wert einer Glühlampe liegt bei etwa 5 Prozent. <br> | ||
| Zeile 81: | Zeile 72: | ||
b) Berechne, wie viel Energie in einer Sekunde wirklich in Form von Licht abgegeben wird.<br> | b) Berechne, wie viel Energie in einer Sekunde wirklich in Form von Licht abgegeben wird.<br> | ||
c) Berechne, wie viel Energie man bei einer LED-Lampe in Form von elektrischer Energie pro Sekunde zuführen müsste, um die gleiche Menge an Licht zu erreichen. Eine kleine LED-Lampe hat einen Wirkungsgrad von etwa 15%. | c) Berechne, wie viel Energie man bei einer LED-Lampe in Form von elektrischer Energie pro Sekunde zuführen müsste, um die gleiche Menge an Licht zu erreichen. Eine kleine LED-Lampe hat einen Wirkungsgrad von etwa 15%. | ||
|Arbeitsmethode | |||
}} | }} | ||
{{ | {{Box | ||
|Aufgabe 4.4 Elektroauto und Diesel-Auto | |||
| | |||
Elektroautos fahren ohne Abgase. Naja, wenigstens kommen keine aus ihrem Auspuff. Natürlich muss aber die Energie für ein Elektroauto irgendwo herkommen. Im Idealfall aus erneuerbaren Energien wie Wind- oder Sonnenenergie. | Elektroautos fahren ohne Abgase. Naja, wenigstens kommen keine aus ihrem Auspuff. Natürlich muss aber die Energie für ein Elektroauto irgendwo herkommen. Im Idealfall aus erneuerbaren Energien wie Wind- oder Sonnenenergie. | ||
Nehmen wir aber einmal an, die Energie zum Laden käme aus einem Ölkraftwerk (Wirkungsgrad: ca. 45%). Mit dem Strom würde ein Lithium-Ionen-Akku aufgeladen werden, der dann die Energie später an den Elektromotor des Fahrzeugs abgibt. Der Akku wärmt sich beim Laden und Entladen auf und hat dabei einen Wirkungsgrad von nur 90%. Gute Elektromotoren haben einen Wirkungsgrad von ca. 95%. | Nehmen wir aber einmal an, die Energie zum Laden käme aus einem Ölkraftwerk (Wirkungsgrad: ca. 45%). Mit dem Strom würde ein Lithium-Ionen-Akku aufgeladen werden, der dann die Energie später an den Elektromotor des Fahrzeugs abgibt. Der Akku wärmt sich beim Laden und Entladen auf und hat dabei einen Wirkungsgrad von nur 90%. Gute Elektromotoren haben einen Wirkungsgrad von ca. 95%. | ||
Ein Dieselmotor in einem modernen Auto hat einen Wirkungsgrad von ca. 40%. | Ein Dieselmotor in einem modernen Auto hat einen Wirkungsgrad von ca. 40%. | ||
Vergleiche die beiden Fahrzeugtypen hinsichtlich ihres Wirkungsgrades vom Brennstoff zur Fortbewegung. | Vergleiche die beiden Fahrzeugtypen hinsichtlich ihres Wirkungsgrades vom Brennstoff zur Fortbewegung. | ||
|Arbeitsmethode | |||
}} | }} | ||
{{Lernpfad Energie}} | {{Lernpfad Energie}} | ||
[[Kategorie:Physik]] | |||
[[Kategorie:Energie]] | |||
[[Kategorie:Sekundarstufe 1]] | |||
Aktuelle Version vom 23. April 2022, 16:15 Uhr
Reibung - ein "Energie-Leck"
Würde man unser Beispiel ernst nehmen, müsste unser Skater nur rechts oben starten und könnte dann im Grunde stundenlang hin- und herfahren, ohne sich anzustrengen. Ständig würde potentielle Energie in kinetische Energie umgewandelt und umgekehrt. Es ist klar: in der Wirklichkeit funktioniert das so nicht. Ein Skater, der einfach nur auf dem Skateboard hin- und her rollt, wird mit der Zeit immer geringere Höhen an den höchsten Punkten erreichen. Auch wird er im tiefsten Punkt immer langsamer rollen.
Was ist dann aber mit unserem "Glaubenssatz" von der Energieerhaltung, der sich unserem Beispiel mit den Wassergläsern so ausgedrückt hatte, dass beim "Umschütten" von einem Glas ins andere keine Flüssigkeit verloren geht. Ist dieser "Glaubenssatz" jetzt einfach falsch - oder können wir ihn noch "retten".
Was auf jeden Fall nicht mehr funktioniert ist das Bild mit nur zwei Wassergläsern und der immer gleichen Menge Flüssigkeit, die sich irgendwie auf die beiden Gläser verteilt.
Spätestens dann, wenn der Skater wegen der Reibung praktisch zur Ruhe gekommen ist, wären die beiden Gläser in unserem Bild leer; die Flüssigkeit hätte im Laufe der Zeit irgendwie verloren gehen müssen (sozusagen verschüttet worden sein).
Wir können das Bild aber retten, indem wir einen weiteren Behälter für unsere erfinden, in dem wir die (verloren geglaubte oder verschüttete) "Energieflüssigkeit" auffangen.
Der Energieerhaltungssatz gilt also noch immer. Allerdings kommt nun die Energieform der Wärme hinzu. Formuliere den Energieerhaltungssatz nun unter Berücksichtigung von Reibung in Deinem Lerntagebuch als Formel für die Punkte A, B und C. Wir nehmen an, dass alle Energie, die durch Reibung umgewandelt wird, an Ende zu einer Energieform beiträgt, die man Wärmeenergie EWärme nennt.
Der Wirkungsgrad -- ein Maß für effiziente Energieumwandlung
Ein Rechenbeispiel
Wenn sich unser Skater an den oberen Rand der Halfpipe stellt und sich losrollen lässt, so verfolgt er damit ein bestimmtes Ziel: Er will schneller werden. Durch die Reibung wird er allerdings nicht ganz so viel schneller, wie er es sich vielleicht wünscht. Wie stark die Reibung ist, hängt dabei von vielen Einflüssen ab; vor allem aber auch von den Lagern seines Skateboards und von der Oberfläche Halfpipe. Wir können davon ausgehen, dass durch Reibung letztlich Energie in Wärmeenergie umgewandelt wird. Das kann auch über Umwege passieren: ein Skateboard rollt nicht lautlos und auch der Schall trägt Energie weg. Diese wird dann irgendwo in der Umgebung wieder durch Reibung ebenfalls in Wärme umgewandelt. Die Wärmeenergie ist im Falle unseres Skaters ein unerwünschtes "Abfallprodukt".
Wir betrachten nochmal den Fall, dass unser Skater aus einer Höhe von 2,5 Meter in der Halfpipe nach unten fährt.
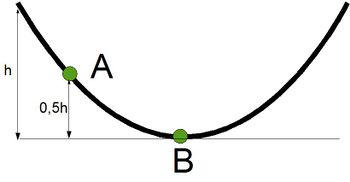
Im Punkt B wird seine Geschwindigkeit gemessen; sie beträgt 5 Meter pro Sekunde.
a) Nenne die Energieformen, in die die Lageenergie umgewandelt wird.
b) Berechne, wie viel der ursprünglich als Lageenergie gespeicherten Energie bei Erreichen von Punkt B als zusätzliche Wärmeenergie vorliegt.
Trotz Reibung bleibt die Gesamtenergie, also die Summe von Lageenergie, Bewegungsenergie und in diesem Fall Wärmeenergie, erhalten. Die Lageenergie und die Bewegungsenergie kann man sowohl am Startpunkt als auch in Punkt B leicht errechnen. Die Differenz an Wärmeenergie
kann man so leicht ausrechnen.
c) Berechne das Verhältnis von Bewegungsenergie am Punkt B zur Lageenergie beim Start.
d) Beschreibe, was kannst Du über die physikalische Einheit dieses Verhältnisses sagen kannst?
Allgemeine Definition: Wirkungsgrad
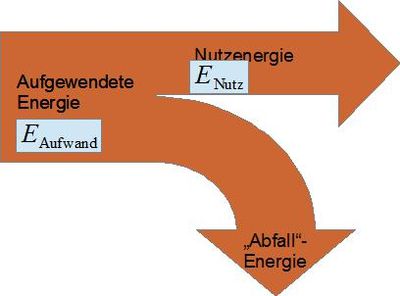
Wenn bei einer Energieumwandlung eine Energieform in mehrere andere umgewandelt wird, von denen manche nützlich sind und andere eher als "Abfallprodukt" gelten, definiert man den so genannten Wirkungsgrad (griech. "eta"). Dieser wird manchmal auch als "Effizienz" bezeichnet (das erklärt auch die Wahl des griechischen Buchstabens.
Im Falle unseres Skaters entspricht die aufgewendete Energie gerade der Lageenergie am Anfang, die "Nutz-Energie" der Bewegungsenergie im Punkt B. Bei Aufgabe c) hast Du also bereits den Wirkungsgrad ausgerechnet. Und wahrscheinlich erkannt, dass sich die Einheiten wegkürzen, dass der Wirkungsgrad also eine der wenigen Größen in der Physik ist, die tatsächlich keine Maßeinheit haben.
Wirkungsgrad im Alltag
Eine 12W-Glühlampe wandelt innerhalb einer Sekunde 12 Joule elektrischer Energie in Lichtenergie um. Naja, jedenfalls teilweise. Denn der typische Wert einer Glühlampe liegt bei etwa 5 Prozent.
a) Stelle eine Vermutung an, welche Energieform außer elektrischer Energie und Licht bei Lampen eine Rolle spielt?
b) Berechne, wie viel Energie in einer Sekunde wirklich in Form von Licht abgegeben wird.
c) Berechne, wie viel Energie man bei einer LED-Lampe in Form von elektrischer Energie pro Sekunde zuführen müsste, um die gleiche Menge an Licht zu erreichen. Eine kleine LED-Lampe hat einen Wirkungsgrad von etwa 15%.
Elektroautos fahren ohne Abgase. Naja, wenigstens kommen keine aus ihrem Auspuff. Natürlich muss aber die Energie für ein Elektroauto irgendwo herkommen. Im Idealfall aus erneuerbaren Energien wie Wind- oder Sonnenenergie. Nehmen wir aber einmal an, die Energie zum Laden käme aus einem Ölkraftwerk (Wirkungsgrad: ca. 45%). Mit dem Strom würde ein Lithium-Ionen-Akku aufgeladen werden, der dann die Energie später an den Elektromotor des Fahrzeugs abgibt. Der Akku wärmt sich beim Laden und Entladen auf und hat dabei einen Wirkungsgrad von nur 90%. Gute Elektromotoren haben einen Wirkungsgrad von ca. 95%. Ein Dieselmotor in einem modernen Auto hat einen Wirkungsgrad von ca. 40%. Vergleiche die beiden Fahrzeugtypen hinsichtlich ihres Wirkungsgrades vom Brennstoff zur Fortbewegung.