Lernpfad Energie/Ein sportliches Beispiel auf der Erde: Unterschied zwischen den Versionen
Main>Peterdauscher |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (48 dazwischenliegende Versionen von 10 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Ein Skateboard auf der Halfpipe== | |||
== Ein Skateboard auf der Halfpipe == | |||
[[Datei:Mini-Vendargues.jpg|miniatur|Halfpipe]] | [[Datei:Mini-Vendargues.jpg|miniatur|Halfpipe]] | ||
| Zeile 7: | Zeile 6: | ||
Im Physiksaal kann man die Situation in etwa nachstellen, wenn man ein Massestück an einem Faden als Pendel aufhängt und hin- und herschwingen lässt. Das Massestück entspricht dem Skateboard-Fahrer, der Faden sorgt, ähnlich wie die Fahrbahn der Halfpipe, dafür, dass sich beim Schwingen die Höhe ändert. | Im Physiksaal kann man die Situation in etwa nachstellen, wenn man ein Massestück an einem Faden als Pendel aufhängt und hin- und herschwingen lässt. Das Massestück entspricht dem Skateboard-Fahrer, der Faden sorgt, ähnlich wie die Fahrbahn der Halfpipe, dafür, dass sich beim Schwingen die Höhe ändert. | ||
{{Box | |||
{{ | |Aufgabe 3.1: Energie in der Halfpipe | ||
| | |||
Was geschieht eigentlich mit der Energie des Skaters beim Einstieg in die Halfpipe? | Was geschieht eigentlich mit der Energie des Skaters beim Einstieg in die Halfpipe? | ||
Schau Dir das folgende Youtube-Video an! Bearbeite danach den auf das Video folgenden Lückentext und die Zuordnungsaufgaben. | Schau Dir das folgende Youtube-Video an! Bearbeite danach den auf das Video folgenden Lückentext und die Zuordnungsaufgaben. | ||
|Arbeitsmethode | |||
}} | |||
{{# | |||
{{#ev:youtube|VwMSsicKRYI|800|center}} | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 21: | Zeile 22: | ||
</div> | </div> | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
<big>'''Weitere Aufgaben'''</big><br> | <big>'''Weitere Aufgaben'''</big><br> | ||
| Zeile 27: | Zeile 28: | ||
{| | {| | ||
|- | |- | ||
| [[Datei:LE2-Halfpipe-energy1.jpg|LE2-Halfpipe-energy1|100px]] || [[Datei:LE2-Halfpipe-glass1.jpg|LE2-Halfpipe-glass1|100px]] | |[[Datei:LE2-Halfpipe-energy1.jpg|LE2-Halfpipe-energy1|100px]]||[[Datei:LE2-Halfpipe-glass1.jpg|LE2-Halfpipe-glass1|100px]] | ||
|- | |- | ||
| [[Datei:LE2-Halfpipe-energy2.jpg|LE2-Halfpipe-energy2|100px]] || [[Datei:LE2-Halfpipe-glass4.jpg|LE2-Halfpipe-glass4|100px]] | |[[Datei:LE2-Halfpipe-energy2.jpg|LE2-Halfpipe-energy2|100px]]||[[Datei:LE2-Halfpipe-glass4.jpg|LE2-Halfpipe-glass4|100px]] | ||
|- | |- | ||
| [[Datei:LE2-Halpipe-energy3.jpg|LE2-Halpipe-energy3|100px]] || [[Datei:LE2-Halfpipe-glass2.jpg|LE2-Halfpipe-glass2|100px]] | |[[Datei:LE2-Halpipe-energy3.jpg|LE2-Halpipe-energy3|100px]]||[[Datei:LE2-Halfpipe-glass2.jpg|LE2-Halfpipe-glass2|100px]] | ||
|- | |- | ||
| [[Datei:LE2-Halpipe-energy4.jpg|LE2-Halpipe-energy4|100px]] || [[Datei:LE2-Halfpipe-glass3.jpg|LE2-Halfpipe-glass3|100px]] | |[[Datei:LE2-Halpipe-energy4.jpg|LE2-Halpipe-energy4|100px]]||[[Datei:LE2-Halfpipe-glass3.jpg|LE2-Halfpipe-glass3|100px]] | ||
|} | |} | ||
</div> | </div> | ||
== | ==Energieerhaltung: Eine Glaubensfrage== | ||
{{Box | |||
{{ | |Aufgabe 3.2 Der Energieerhaltungssatz | ||
| | |||
Zitat aus Wkipedia (http://de.wikipedia.org/wiki/Energieerhaltungssatz; 30.01.2015) | Zitat aus Wkipedia (http://de.wikipedia.org/wiki/Energieerhaltungssatz; 30.01.2015) | ||
| Zeile 49: | Zeile 49: | ||
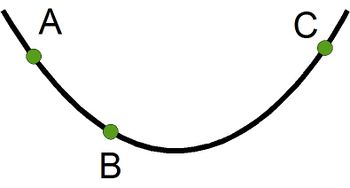
[[Bild:LE3 Halfpipe mit Buchstaben2.jpg|350px]] | [[Bild:LE3 Halfpipe mit Buchstaben2.jpg|350px]] | ||
}} | |||
Formuliere den Energieerhaltungssatz nun in Deinem Lerntagebuch als Formel für die Punkte A, B und C für die Energien E<sub>kin</sub> und E<sub>pot</sub>. Z.B. E<sub>kin,A</sub> soll die kinetische Energie im Punkt A sein. | |||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Die kinetische Energie hier bitte jeweils an erster Stelle aufführen. | Die kinetische Energie hier bitte jeweils an erster Stelle aufführen. | ||
'''E<sub>kin,A</sub>'''+'''E<sub>pot,A</sub>'''='''E<sub>kin,B</sub>'''+ '''E<sub>pot,B</sub>'''='''E<sub>kin,C</sub>'''+ '''E<sub>pot,C</sub>''' | '''E<sub>kin,A</sub>'''+'''E<sub>pot,A</sub>'''='''E<sub>kin,B</sub>'''+ '''E<sub>pot,B</sub>'''='''E<sub>kin,C</sub>'''+ '''E<sub>pot,C</sub>''' | ||
</div> | </div> | ||
==Energieumwandlung: Wie schnell wird der Skater eigentlich?== | |||
Ein Skater startet in einer Halfpipe ganz rechts oben (Höhe h). | Ein Skater startet in einer Halfpipe ganz rechts oben (Höhe h=2,5m über dem tiefsten Punkt der Halfpipe). | ||
{{Box | |||
|Aufgabe 3.3: Berechnen von Geschwindigkeiten mit Hilfe der Energie | |||
| | |||
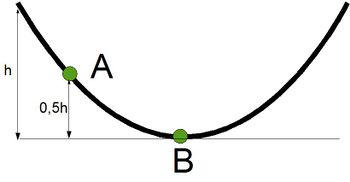
[[Bild:LE3 halfpipe mit Buchstaben und Höhen2.jpg|350px]] | [[Bild:LE3 halfpipe mit Buchstaben und Höhen2.jpg|350px]] | ||
Berechne unter Zuhilfenahme des Energieerhaltungssatzes | Berechne unter Zuhilfenahme des Energieerhaltungssatzes | ||
a) die Geschwindigkeit des Skaters, wenn er sich am Punkt B in der Halfpipe befindet. | a) die Geschwindigkeit des Skaters, wenn er sich am Punkt B in der Halfpipe befindet. | ||
b) die Geschwindigkeit des Skaters, wenn er sich am Punkt A, also auf halber Höhe (1,25m) befindet? | b) die Geschwindigkeit des Skaters, wenn er sich am Punkt A, also auf halber Höhe (1,25m) befindet? | ||
Mit der Simulation https://phet.colorado.edu/sims/html/energy-skate-park/latest/energy-skate-park_de.html kannst Du nachprüfen, ob Deine Ergebnisse tatsächlich richtig sind. Lasse alle Einstellungen (Schieberegler) gleich und kreuze nur "Gitternetz" und "Geschwindigkeit" an. | |||
|Arbeitsmethode | |||
}} | }} | ||
{{Lösung versteckt|1= | |||
:Lösung a) 7m/s | |||
:Lösung b) 5m/s | |||
{{ | |||
}} | }} | ||
Wenn Ihr ein falsches Ergebnis herausbekommen habt und die Fehlerursache nicht finden könnt, wendet Euch an Euren Lehrer! | |||
==Der neueste Trend: Die Crazy-Pipe== | |||
== | |||
Die normale Halfpipe kennt jeder. Ein Konstrukteur präsentiert für einen neuen Skatepark eine asymmetrische Halfpipe. Eine etwas steilere Hälfte dieser neuen Version soll den Skatern den ultimativen Kick bescheren. Der Konstrukteur behauptet, mit seiner Crazy-Pipe komme der Skater auf der anderen Seite wesentlich höher, weil hier ja der Weg deutlich kürzer sei. | Die normale Halfpipe kennt jeder. Ein Konstrukteur präsentiert für einen neuen Skatepark eine asymmetrische Halfpipe. Eine etwas steilere Hälfte dieser neuen Version soll den Skatern den ultimativen Kick bescheren. Der Konstrukteur behauptet, mit seiner Crazy-Pipe komme der Skater auf der anderen Seite wesentlich höher, weil hier ja der Weg deutlich kürzer sei. | ||
{{Box | |||
{{ | |Aufgabe 3.4: Die Crazy Pipe | ||
| | |||
Du bist vom Planungsbüro des Skateparks zum Gutachter ernannt worden. | Du bist vom Planungsbüro des Skateparks zum Gutachter ernannt worden. | ||
| Zeile 121: | Zeile 94: | ||
Schreibe ein Gutachten, in dem du zur Behauptung des Konstrukteurs Stellung nimmst. Dein Gutachten muss stichhaltig und gut nachvollziehbar sein. Schließlich hängen von einem solchen Gutachten häufig große Geldsummen ab. Ein falsches Gutachten kann also einen großen finanziellen Schaden anrichten. Du solltest sowohl den (unrealistischen) Fall ohne Reibung als auch den (realistischen) Fall mit Reibung in deinem Gutachten erörtern. | Schreibe ein Gutachten, in dem du zur Behauptung des Konstrukteurs Stellung nimmst. Dein Gutachten muss stichhaltig und gut nachvollziehbar sein. Schließlich hängen von einem solchen Gutachten häufig große Geldsummen ab. Ein falsches Gutachten kann also einen großen finanziellen Schaden anrichten. Du solltest sowohl den (unrealistischen) Fall ohne Reibung als auch den (realistischen) Fall mit Reibung in deinem Gutachten erörtern. | ||
|Arbeitsmethode | |||
}} | }} | ||
== | ==Weitere-Aufgaben== | ||
{{Box | |||
|Aufgabe 3.5: Freier Fall | |||
| | |||
Ein Stein fällt von einem 20 Meter hohen Aussichtsturm. Bestimme (ohne die Berücksichtigung von Reibung) die Geschwindigkeit, mit der er auf dem Boden aufschlägt. | |||
|Arbeitsmethode}} | |||
{{Box | |||
|Aufgabe 3.6: Senkrechter Wurf | |||
| | |||
Ein Stein wird von einem 20 Meter hohen Aussichtsturm einmal mit 5m/s nach unten geworfen, einmal mit 5m/s nach unten. Bestimme für beide Fälle (ohne die Berücksichtigung von Reibung) die Geschwindigkeit, mit der er auf dem Boden aufschlägt. Vergleiche die Ergebnisse untereinander und mit dem Ergebnis von Aufgabe 3.5. | |||
|Arbeitsmethode}} | |||
{{Box | |||
|Aufgabe 3.7: Im Leerlauf bergauf | |||
| | |||
Ein Fahrradfahrer hat in der Ebene sein Fahrrad auf 35km/h beschleunigt. Er hört auf, in die Pedale zu treten und lässt sein Fahrrad an einem Hügel auslaufen. Berechne, wie viel Höhe er gewinnen könnte, wenn das Fahrrad ohne Reibung den Hügel hinauffahren würde. | |||
|Arbeitsmethode}} | |||
{{Box | |||
|Aufgabe 3.8: Freier Fall auf halbem Wege | |||
| | |||
Ein Stein fällt von einem 40 Meter hohen Turm. | |||
Jemand behauptet: Auf 20 Metern Höhe hat er die Hälfte der Geschwindigkeit erreicht, die er kurz vor dem Aufprall hat. Untersuche die Behauptung auf Richtigkeit und schreibe ein begründetes fachliches Gutachten. | |||
|Arbeitsmethode}} | |||
{{Lernpfad Energie}} | |||
[[Kategorie:Physik]] | |||
[[Kategorie:Interaktive Übung]] | |||
[[Kategorie:R-Quiz]] | |||
Aktuelle Version vom 23. April 2022, 16:15 Uhr
Ein Skateboard auf der Halfpipe
Auf einer Halfpipe können Skateboard-Akrobaten ihr Können unter Beweis stellen. Das Befahren einer solchen Halfpipe hat ganz viel mit kinetischer und potentieller Energie zu tun.
Im Physiksaal kann man die Situation in etwa nachstellen, wenn man ein Massestück an einem Faden als Pendel aufhängt und hin- und herschwingen lässt. Das Massestück entspricht dem Skateboard-Fahrer, der Faden sorgt, ähnlich wie die Fahrbahn der Halfpipe, dafür, dass sich beim Schwingen die Höhe ändert.
Was geschieht eigentlich mit der Energie des Skaters beim Einstieg in die Halfpipe?
Schau Dir das folgende Youtube-Video an! Bearbeite danach den auf das Video folgenden Lückentext und die Zuordnungsaufgaben.
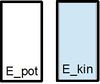
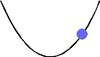
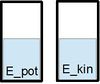
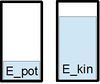
Die Energie, welche in der Lage des Skateboards zur Erde steckt, wandelt sich während des Durchfahrens der Halfpipe um. Wenn der Skater ganz oben ist und sich noch nicht bewegt, liegt noch die gesamte Energie als Lagenergie oder auch potenzielle Energie Epot vor. Während der Abwärtsbewegung wandelt sich die Lageenergie nach und nach um in Bewegungsenergie oder auch kinetische Energie Ekin. Auf der Zwischenstrecke ist die Gesamtenergie auf beide Energieformen verteilt. An der tiefsten Stelle der Halfpipe hat sich die gesamte Energie in Bewegungsenergie umgewandelt. Jetzt wird bei der nun folgenden Aufwärtsbewegung die Bewegungsenergie wieder in Lageenergie umgewandelt. Wir haben bisher nur diese beiden Energieformen betrachtet. Auch gibt es bei unserem gedachten Skateboard keine Reibung, was natürlich nicht realistisch ist.
Weitere Aufgaben
Ordne die Energien (symbolisiert als Flüssigkeit in Wassergläsern) und die aktuellen Positionen des Skaters richtig zu.
 |
|
 |
|
 |
|
 |
|
Energieerhaltung: Eine Glaubensfrage
Zitat aus Wkipedia (http://de.wikipedia.org/wiki/Energieerhaltungssatz; 30.01.2015)
"Der Energieerhaltungssatz besagt, dass die Summe aller Energien eines isolierten Systems sich nicht mit der Zeit ändert. Zwar kann Energie zwischen verschiedenen Energieformen umgewandelt werden, beispielsweise von Bewegungsenergie in Wärmeenergie. Es ist jedoch nicht möglich, innerhalb eines abgeschlossenen Systems Energie zu erzeugen oder zu vernichten: Die Energie ist eine Erhaltungsgröße.
Die Gesamtenergie in einem abgeschlossenen System bleibt konstant. Unter einem abgeschlossenen System versteht man ein System ohne Energie-, Informations- oder Stoffaustausch und ohne Wechselwirkung mit der Umgebung."
Formuliere den Energieerhaltungssatz nun in Deinem Lerntagebuch als Formel für die Punkte A, B und C für die Energien Ekin und Epot. Z.B. Ekin,A soll die kinetische Energie im Punkt A sein.
Die kinetische Energie hier bitte jeweils an erster Stelle aufführen. Ekin,A+Epot,A=Ekin,B+ Epot,B=Ekin,C+ Epot,C
Energieumwandlung: Wie schnell wird der Skater eigentlich?
Ein Skater startet in einer Halfpipe ganz rechts oben (Höhe h=2,5m über dem tiefsten Punkt der Halfpipe).
Berechne unter Zuhilfenahme des Energieerhaltungssatzes a) die Geschwindigkeit des Skaters, wenn er sich am Punkt B in der Halfpipe befindet. b) die Geschwindigkeit des Skaters, wenn er sich am Punkt A, also auf halber Höhe (1,25m) befindet?
Mit der Simulation https://phet.colorado.edu/sims/html/energy-skate-park/latest/energy-skate-park_de.html kannst Du nachprüfen, ob Deine Ergebnisse tatsächlich richtig sind. Lasse alle Einstellungen (Schieberegler) gleich und kreuze nur "Gitternetz" und "Geschwindigkeit" an.
- Lösung a) 7m/s
- Lösung b) 5m/s
Wenn Ihr ein falsches Ergebnis herausbekommen habt und die Fehlerursache nicht finden könnt, wendet Euch an Euren Lehrer!
Der neueste Trend: Die Crazy-Pipe
Die normale Halfpipe kennt jeder. Ein Konstrukteur präsentiert für einen neuen Skatepark eine asymmetrische Halfpipe. Eine etwas steilere Hälfte dieser neuen Version soll den Skatern den ultimativen Kick bescheren. Der Konstrukteur behauptet, mit seiner Crazy-Pipe komme der Skater auf der anderen Seite wesentlich höher, weil hier ja der Weg deutlich kürzer sei.
Du bist vom Planungsbüro des Skateparks zum Gutachter ernannt worden.
Schreibe ein Gutachten, in dem du zur Behauptung des Konstrukteurs Stellung nimmst. Dein Gutachten muss stichhaltig und gut nachvollziehbar sein. Schließlich hängen von einem solchen Gutachten häufig große Geldsummen ab. Ein falsches Gutachten kann also einen großen finanziellen Schaden anrichten. Du solltest sowohl den (unrealistischen) Fall ohne Reibung als auch den (realistischen) Fall mit Reibung in deinem Gutachten erörtern.
Weitere-Aufgaben
Ein Stein fällt von einem 20 Meter hohen Aussichtsturm. Bestimme (ohne die Berücksichtigung von Reibung) die Geschwindigkeit, mit der er auf dem Boden aufschlägt.
Ein Stein wird von einem 20 Meter hohen Aussichtsturm einmal mit 5m/s nach unten geworfen, einmal mit 5m/s nach unten. Bestimme für beide Fälle (ohne die Berücksichtigung von Reibung) die Geschwindigkeit, mit der er auf dem Boden aufschlägt. Vergleiche die Ergebnisse untereinander und mit dem Ergebnis von Aufgabe 3.5.
Ein Fahrradfahrer hat in der Ebene sein Fahrrad auf 35km/h beschleunigt. Er hört auf, in die Pedale zu treten und lässt sein Fahrrad an einem Hügel auslaufen. Berechne, wie viel Höhe er gewinnen könnte, wenn das Fahrrad ohne Reibung den Hügel hinauffahren würde.
Ein Stein fällt von einem 40 Meter hohen Turm. Jemand behauptet: Auf 20 Metern Höhe hat er die Hälfte der Geschwindigkeit erreicht, die er kurz vor dem Aufprall hat. Untersuche die Behauptung auf Richtigkeit und schreibe ein begründetes fachliches Gutachten.