Zentrische Streckung/Vierstreckensatz/2.Station

1. Station: Erster Vierstreckensatz - Schenkellösung - 2. Station: Erster Vierstreckensatz - Abschnittlösung - 3. Station: Zweiter Vierstreckensatz - 4. Station: Zusammenfassung - 5. Station: Übung

2. Station: Erster Vierstreckensatz - Abschnittlösung

Bei dieser Aufgabe sollst du berechnen, wie weit Dia von Panto entfernt ist. Die gesuchte Größe ist hier nur ein
Abschnitt des Schenkels.

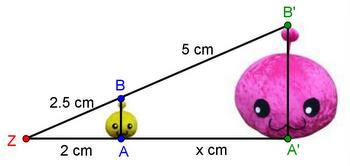
Anhand der Eigenschaft der Längenverhältnisstreue der zentrischen Streckung kannst du auch hier wieder die geeignete Formel
zur Berechnung der unbekannten Strecke herleiten. Setze dafür die richtige Aussage in die passende Lücke ein:

$\overline{ZA'} =$ $|k| \cdot \overline{ZA}$ $\mathit{und}\ \overline{ZB'} =$ $|k| \cdot \overline{ZB}$
$\overline{AA'} = \overline{ZA'} - \overline{ZA}\ \mathit{und}\ \overline{BB'} = \overline{ZB'} - \overline{ZB}$
Erste Zeile in zweite Zeile eingesetzt ergibt:
$\overline{AA'} =$ $|k| \cdot \overline{ZA} - \overline{ZA}$ $\mathit{und}\ \overline{BB'} =$ $|k| \cdot \overline{ZB} - \overline{ZB}$
Aufgelöst nach |k|:
$\mid k\mid =$ ${\overline{AA'}\over\overline{ZA}}$ $- {\overline{ZA}\over\overline{ZA}}$ $\mathit{und}\ \mid k\mid =$ ${\overline{BB'}\over\overline{ZB}} -$${\overline{ZB}\over\overline{ZB}}$
$\mid k\mid =$ ${\overline{AA'}\over\overline{ZA}} - 1$ $\mathit{und}$ $\mid k\mid$ $= {\overline{BB'}\over\overline{ZB}} - 1$
Gleichsetzen:
${\overline{AA'}\over\overline{ZA}} - 1 =$ ${\overline{BB'}\over\overline{ZB}}$ $- 1 \mid+1$
${\overline{AA'}\over\overline{ZA}} =$ ${\overline{BB'}\over\overline{ZB}}$

 

Du hast die Abschnittlösung des ersten Vierstreckensatzes hergeleitet.

Auch hier verhalten sich die Abschnitte auf der einen Halbgeraden wie die Abschnitte auf der anderen Halbgeraden.

Trage hier deine Lösung mit Angabe der Einheit (cm) ein!

${x \over 2\ cm} = {5\ cm \over 2,5\ cm}$
Berechne das Ergebnis mit dem Taschenrechner:
x = 4 cm (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).

 

$\Rightarrow$ Weiter zur 3. Station: Zweiter Vierstreckensatz

$\Leftarrow$ Zurück zur 1. Station: Erster Vierstreckensatz - Schenkellösung